Cinématique rotationnelle - Physique 298

« Les hommes parlent de tuer le temps, alors que le temps les tue tranquillement »
Dion Boucicault – London Assurance (1841)

Jusqu’à présent, nous avons considéré la cinématique et la dynamique des particules, y compris le mouvement de translation et le mouvement circulaire, ainsi que le mouvement de translation des systèmes de particules (en particulier les corps rigides) en termes de mouvement du centre de masse du système (corps). Dans ce dernier cas, nous pouvons imaginer que toute la masse de l’objet est située au centre de masse en ce qui concerne les forces de translation externes.

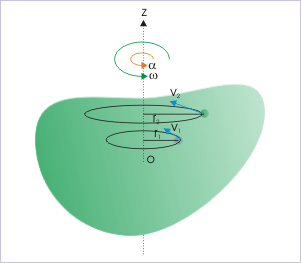L’étape suivante consiste à considérer la rotation d’un corps rigide autour d’un axe de rotation fixe. Notez que, puisque nous considérons un corps rigide, chaque particule du corps reste fixe par rapport aux autres. Cela signifie que dans un tel mouvement de rotation, chaque particule se déplace dans un cercle dont le centre se trouve sur l’axe de rotation. Dans le schéma de droite, l’objet tourne autour de l’axe z ; les deux particules de l’échantillon se déplacent dans des cercles de rayons r1 et r2. Si nous pouvons décrire le mouvement circulaire d’une particule, sans référence directe à son rayon, alors toutes les particules du système seront décrites par le même ensemble d’équations. Bien que les rayons des particules soient différents, leurs rotations angulaires sont identiques. Il est donc nécessaire d’introduire des variables angulaires.

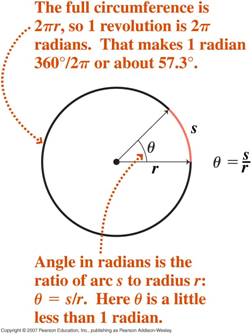
Mesure radiale des angles

Vitesse (vitesse) angulaire et accélération angulaire

La vitesse angulaire et l’accélération angulaire sont définies de manière similaire à la vitesse et à l’accélération. Il existe des valeurs moyennes et instantanées de chacune.

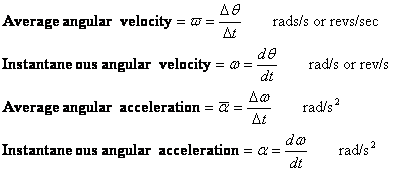
L’accélération angulaire n’est pas la même chose que l’accélération centripète. L’accélération centripète est due à un changement dans la direction de la vitesse, l’accélération angulaire est due à un changement dans la magnitude de la vitesse (par l’angle de rotation).

Exactement comme dans le cas de la translation, la différence entre la vitesse angulaire et la vitesse angulaire est la direction. La vitesse angulaire doit inclure un sens de rotation autour de l’axe en question. Par exemple, 10 rad/s dans le sens horaire autour de l’axe x est une vitesse angulaire, 10 rad/s autour de l’axe x est une vitesse angulaire.

Équations cinématiques de rotation

Par analogie directe avec les équations cinématiques de translation, le mouvement circulaire autour d’un seul axe sous accélération angulaire constante peut être décrit par les quatre équations suivantes,

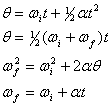
où nous avons effectué les substitutions,

Notez que tout comme +x est défini arbitrairement vers la droite, la valeur positive de thêta peut être définie dans le sens horaire ou antihoraire.

Relation entre les variables angulaires et translationnelles

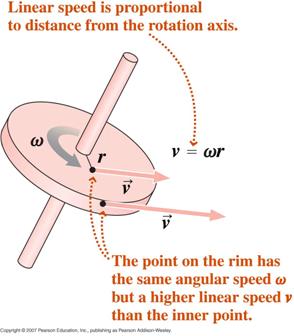En partant de la définition de la mesure radian, en différenciant par rapport au temps, on peut montrer que,

où v est la vitesse tangentielle et a l’accélération tangentielle.

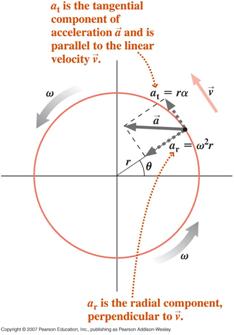
Une particule exécutant un mouvement circulaire, avec une vitesse angulaire variable (mouvement circulaire non uniforme), subira deux composantes d’accélération, une composante tangentielle due au changement de magnitude de sa vitesse et une composante radiale (centripète) due au changement de direction de sa vitesse

L’accélération nette de la particule est la somme vectorielle de ces deux composantes comme indiqué ci-dessous.

Pour votre information…

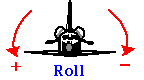
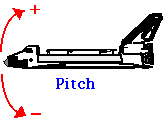
La rotation simultanée autour de plus d’un axe peut être considérée de manière similaire au mouvement du projectile, où nous avons étendu notre discussion de translation 1D au mouvement 2D. Dans les applications aéronautiques, les rotations autour des trois axes sont décrites comme Roll, Pitch et Yaw.