Comment penser avec les exposants et les logarithmes

Voici une astuce pour réfléchir à des problèmes impliquant des exposants et des logarithmes. Il suffit de poser deux questions :

1) Parlons-nous des entrées (cause du changement) ou des sorties (le changement réel qui s’est produit ?)

Les logarithmes révèlent les entrées qui ont causé la croissance
Les exposants trouvent le résultat final de la croissance

2) Parlons-nous du point de vue du cultivateur ou de celui d’un observateur ?

e et le log naturel sont du point de vue instant par instant du cultivateur
La base 10, la base 2, etc. sont des mesures commodes pour un observateur humain

Dans ma tête, je mets les options dans un tableau:

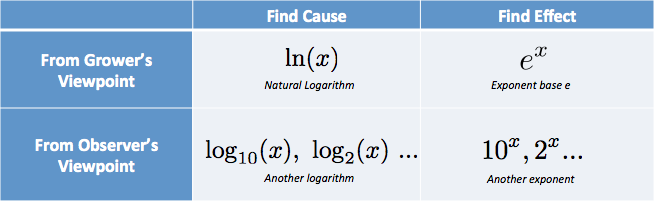
exposant logarithme point de vue comparaison

J’ai des pensées comme « J’ai besoin de la cause, du point de vue du cultivateur… c’est le log naturel. ». (Le logarithme naturel est abrégé avec une minuscule LN, du logarithme naturel de haute voltige.)

J’étais frustré par les cours qui décrivaient la partie interne du tableau, les fonctions brutes, sans les légendes qui expliquaient quand les utiliser !

Cela ne passera pas, ayons une pratique directe de la pensée avec les logarithmes et les exposants.

Scénario : Décrire la croissance du PIB

Voici un exemple typique de croissance:

De 2000 à 2010, le PIB américain est passé de 9,9 trillions à 14,4 trillions

Ok, bien sûr, ces chiffres montrent que le changement s’est produit. Mais nous voulons probablement avoir un aperçu de la cause : Quel taux de croissance annuel moyen expliquerait ce changement ?

Immédiatement, mon cerveau pense « logarithmes » parce que nous travaillons à rebours de la croissance au taux qui l’a causée. Je commence par une pensée comme celle-ci :

$\displaystyle{\text{logarithme du changement}. \rightarrow \text{cause de la croissance} }$

Un bon début, mais affinons-le.

Premièrement, quel logarithme devons-nous utiliser ?

Par défaut, je choisis le logarithme naturel. La plupart des événements finissent par être en termes de cultivateur (et non d’observateur), et j’aime « chevaucher » avec l’élément en croissance pour visualiser ce qui se passe. (Les radian sont similaires : ils mesurent les angles en termes de celui qui bouge.)

Question suivante : à quel changement appliquons-nous le logarithme ?

Nous sommes vraiment juste intéressés par le rapport entre le début et la fin : 9,9 trillions à 14,4 trillions en 10 ans. C’est le même taux de croissance que de passer de 9,90 \$ à 14,40 \$ dans la même période.

Nous pouvons affiner notre pensée:

$\displaystyle{\text{logarithme naturel du rapport de croissance}. \rightarrow \text{cause de la croissance} }$

$\displaystyle{\ln(\frac{14.4}{9.9}) = .374}$

Ok, la cause était un taux de .374 ou 37.4%. Avons-nous fini ?

Pas encore. Les logarithmes ne savent pas combien de temps un changement a pris (nous n’avons pas branché 10 ans, n’est-ce pas ?). Ils nous donnent un taux comme si tout le changement se produisait dans une seule période de temps.

Le changement pourrait en effet être une seule année de croissance continue de 37,4%, ou 2 années de croissance de 18,7%, ou une autre combinaison.

D’après le scénario, nous savons que le changement a pris 10 ans, donc le taux a dû être :

$\displaystyle{ \text{rate} = \frac{.374}{10} = .0374 = 3.74\%}$

Du point de vue de la croissance instantanée et continue, l’économie américaine a augmenté de 3.74% par an.

A-t-on fini maintenant ? Pas tout à fait !

Ce taux continu est du point de vue du cultivateur, comme si nous « chevauchions » l’économie au fur et à mesure de son évolution. Un banquier se soucie probablement de la différence d’une année sur l’autre, adaptée aux humains. Nous pouvons le déterminer en laissant la croissance continue se dérouler pendant un an :

$\displaystyle{\text{exposant avec taux et temps}. \rightarrow \text{effet de la croissance} }$

$\displaystyle{e^{\text{rate} \cdot \text{time}} = \text{croissance}}$

$\displaystyle{e^{.0374 \cdot 1} = 1.0381}$

Le gain d’une année sur l’autre est de 3,8%, légèrement supérieur au taux instantané de 3,74% dû à la capitalisation. Voici une autre façon de le dire:

D’instant en instant, une partie donnée de l’économie croît de 3,74%, modélisée par $e^(.0374 * années)$
Sur une base annuelle, avec les effets composés travaillés, l’économie croît de 3,81%, modélisé par 1,0381^années$

En finance, nous pouvons vouloir le changement d’une année sur l’autre qui peut être comparé joliment avec d’autres tendances. En sciences et en ingénierie, nous préférons modéliser le comportement sur une base instantanée.

Scénario : Décrire la croissance naturelle

Je déteste les exemples artificiels comme « Supposons que les bactéries doublent toutes les 24 heures, trouvons sa formule de croissance. ». Les colonies de bactéries se répliquent-elles sur des intervalles humains propres, et devons-nous attendre un doublement exact ?

Un meilleur scénario : « Hé, j’ai trouvé des bactéries, j’ai attendu une heure, et la motte est passée de 2,3 grammes à 2,32 grammes. Je vais déjeuner maintenant. Calculez combien nous aurons quand je serai de retour dans 3 heures. »

Modélisons cela. Nous aurons besoin d’un logarithme pour trouver le taux de croissance, puis d’un exposant pour projeter cette croissance dans le futur. Comme avant, gardons tout en termes de logarithme naturel pour commencer.

Le facteur de croissance est :

$\displaystyle{\text{logarithme de changement}. \N{flèche droite{\N} cause de la croissance} }$

$\displaystyle{\ln(\text{croissance}) = \ln(2,32/2,3) = .0086 = .86\%}$

C’est le taux pour une heure, et le modèle général pour se projeter en avant sera

$\displaystyle{\text{exposant avec taux et temps}. \rightarrow \text{effet de la croissance} }$

$\displaystyle{e^{.0086 \cdot \text{hours}} \N- Flèche droite \N- Effet de la croissance} }$

Si nous commençons avec 2,32 et que nous croissons pendant 3 heures, nous aurons :

$\displaystyle{2,32 \cdot e^{.0086 \cdot 3} = 2,38}$

Juste pour le plaisir, combien de temps avant que la bactérie ne double ? Imaginons que l’on attende que 1 se transforme en 2 :

$\displaystyle{1 \cdot e^{.0086 \cdot \text{hours}} = 2}$

On peut mécaniquement prendre le logarithme naturel des deux côtés pour « annuler l’exposant », mais pensons intuitivement.

Si 2 est le résultat final, alors ln(2) est l’apport de croissance qui nous a amené là (un certain taux × temps). Nous savons que le taux était de 0,0086, donc le temps pour arriver à 2 serait :

$\displaystyle{ \text{hours} = \frac{\ln(2)}{\text{rate}} = \frac{ 0,693}{ 0,0086} = 80,58}$

La colonie doublera après ~80 heures. (Content que tu ne sois pas resté dans le coin ?)

Que signifie vraiment le changement de perspective ?

Déterminer si vous voulez l’entrée (cause de la croissance) ou la sortie (résultat de la croissance) est assez simple. Mais comment visualiser la perspective du cultivateur ?

Imaginez que nous avons des petits travailleurs qui construisent le modèle de croissance final (voir l’article sur les exposants) :

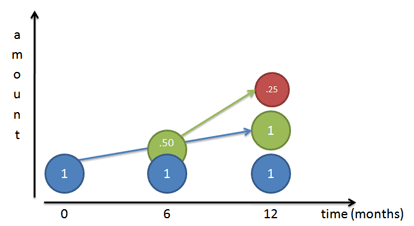
$intérêt composé$

Si notre taux de croissance est de 100%, nous disons à notre travailleur initial (M. Bleu) de travailler régulièrement et de créer une copie à 100% de lui-même d’ici la fin de l’année. Si nous le suivons jour après jour, nous voyons qu’il termine effectivement une copie à 100% de lui-même (M. Vert) à la fin de l’année.

Mais… cet ouvrier qu’il construisait (M. Vert) commence à travailler aussi. Si M. Vert apparaît pour la première fois au bout de 6 mois, il a un semestre pour travailler (même taux annuel que M. Bleu) et il construit M. Rouge. Bien sûr, M. Rouge finit par être à moitié terminé, puisque M. Vert n’a que 6 mois.

Et si M. Vert apparaissait après 4 mois ? Un mois ? Un jour ? Une seconde ? Si les travailleurs commencent à croître immédiatement, nous obtenons la courbe instant par instant définie par $e^x$:

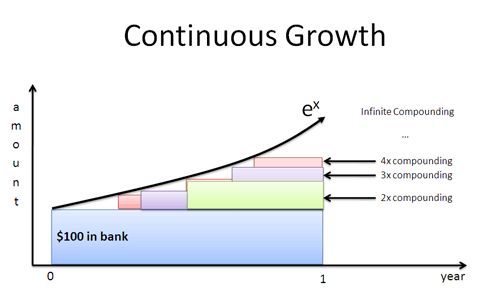
croissance continue

Le logarithme naturel donne un taux de croissance en termes de perspective d’un travailleur individuel. On branche ce taux dans $e^x$ pour trouver le résultat final, avec tous les composés inclus.

Utilisation d’autres bases

Le passage à un autre type de logarithme (base 10, base 2, etc.) signifie que nous recherchons un certain modèle dans la croissance globale, et non pas ce que fait le travailleur individuel.

Chaque logarithme pose une question lorsqu’on voit un changement :

Log base e : Quel était le rythme instantané suivi par chaque ouvrier ?
Log base 2 : Combien de doublements ont été nécessaires ?
Log base 10 : Combien de 10x-ings ont été nécessaires ?

Voici un scénario à analyser :

En 30 ans, le nombre de transistors sur les puces typiques est passé de 1000 à 1 milliard

Comment analyseriez-vous cela ?

Les micro-puces ne sont pas une entité unique qui croît de façon harmonieuse au fil du temps. Elles sont des éditions séparées, d’entreprises concurrentes, et indiquent une tendance technologique générale.
Puisque nous ne « roulons pas » avec une puce électronique en expansion, utilisons une échelle faite pour la commodité humaine. Il est plus facile de penser à un doublement qu’à un décuplement.

Avec ces hypothèses, nous obtenons:

$\displaystyle{\text{logarithme de changement} \rightarrow \text{cause de la croissance} }$

$\displaystyle{\log_2(\frac{\text{1 milliard}}{1000}) = \log_2(\text{1 million}) \sim \text{20 doublements}}$

La « cause de la croissance » était 20 doublements, qui, nous le savons, se sont produits sur 30 ans. Cela fait en moyenne 2/3 doublements par an, soit 1,5 an par doublement – une bonne règle empirique.

Du point de vue du cultivateur, nous calculerions $\ln(\text{1 milliard}/1000) / \text{30 ans} = 46\%$ de croissance continue (un peu plus difficile à relier à ce scénario).

Nous pouvons résumer notre analyse dans un tableau :

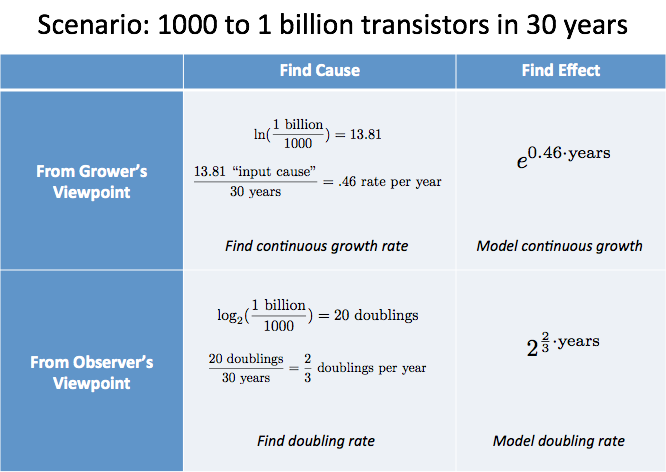
exposants exemple transistor

Résumé

L’apprentissage consiste à trouver les légendes cachées derrière un concept. Quand est-il utilisé ? Quel point de vue apporte-t-il au problème ?

Mon interprétation actuelle est que les exposants posent des questions sur la cause par rapport à l’effet et le cultivateur par rapport à l’observateur. Mais nous n’avons jamais fini ; une partie de l’amusement est de voir comment nous pouvons recapter de vieux concepts.

Happy math.

Annexe : La formule de changement de base

Voici comment penser à changer de base. En supposant un taux de croissance continu de 100%,

ln(x) est le temps pour croître jusqu’à x
ln(2) est le temps pour croître jusqu’à 2

Puisque nous avons le temps pour doubler, nous pouvons voir combien « tiendraient » dans le temps total pour croître jusqu’à x :

$\displaystyle{\text{nombre de doublements de 1 à x} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

Par exemple, combien de doublements se produisent de 1 à 64 ?

Eh bien, ln(64) = 4.158. Et ln(2) = .693. Le nombre de doublements qui correspondent est :

$\displaystyle{\frac{\ln(64)}{\ln(2)} = \frac{4,158}{.693} = 6}$

Dans le monde réel, les calculatrices peuvent perdre en précision, donc utilisez une fonction logarithme direct base 2 si possible. Et bien sûr, on peut avoir un nombre fractionnaire : Passer de 1 à la racine carrée de 2 est la « moitié » d’un doublement, ou log2(1,414) = 0,5.

Le passage au logarithme en base 10 signifie que l’on compte le nombre de multiplications par 10 qui correspondent :

$\displaystyle{\text{nombre de multiplications par 10 de 1 à x} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Super, non ? Lisez Utiliser les logarithmes dans le monde réel pour plus d’exemples.

Autres posts de cette série

Un guide intuitif des fonctions exponentielles & e
Démystifier le logarithme naturel (ln)
Un guide visuel des taux d’intérêt simples, composés et continus
Définitions courantes de e (colorisées)
Comprendre les exposants (Pourquoi 0^0 = 1 ?)
Utiliser les logarithmes dans le monde réel
Comment penser avec les exposants et les logarithmes
Comprendre la croissance discrète par rapport à la croissance continue
Que signifie réellement un exposant ?
Q : Pourquoi e est-il spécial ? (2,718…, et non pas 2, 3,7 ou un autre nombre ?)