
Les réseaux neuronaux et les mathématiques sont inséparables et c’est probablement ce qui effraie la plupart des gens. J’ai entendu une fois de trop des remarques douteuses sur le Deep Learning, « Oh c’est trop de maths pour que je comprenne », « Combien d’entreprises utilisent vraiment le Deep Learning ? ». Je préfère m’épargner le casse-tête et rester loin de ces concepts exigeants ».
Mais si vous y réfléchissez, ce n’est pas si difficile. Faites-moi confiance ! Pour comprendre pourquoi un algorithme se comporte d’une certaine manière, il est essentiel de comprendre ce qui se passe dans les coulisses. Les algorithmes complexes d’apprentissage automatique sont aujourd’hui emballés de manière pratique pour nous et ne sont qu’à un appel de fonction. Les dérivés des fonctions d’activation sont des concepts un peu moins évidents que nous avons souvent tendance à ignorer. Cependant, ils constituent la base d’algorithmes puissants et le fait de faire un petit effort supplémentaire pour les comprendre est certainement payant. Après avoir lu cet article, vous serez un peu plus près de démêler ce qui se cache sous la façade de la « boîte noire ».
Contexte
Les réseaux neuronaux utilisent une variété de fonctions d’activation dans les couches cachées et de sortie pour catalyser le processus d’apprentissage. Quelques fonctions d’activation couramment utilisées incluent les fonctions Sigmoïde et tanH. La fonction d’activation la plus populaire est ReLU ( Rectified Linear Unit) en raison de sa capacité à surmonter efficacement le problème du gradient évanescent. Un aperçu approfondi des fonctions d’activation est pour un autre jour. Aujourd’hui, nous allons nous concentrer sur les mathématiques derrière la dérivée de la fonction Sigmoïde.
Pourquoi la dérivée d’une fonction d’activation est-elle importante ?
Comme vous le savez probablement, deux étapes conduisent les réseaux neuronaux :
- Propagation vers l’avant – Les données d’entrée circulent dans le réseau et nous obtenons la sortie prédite. On la compare à la sortie réelle et on calcule l’erreur.
- Propagation arrière – L’erreur calculée est utilisée pour mettre à jour les paramètres du réseau neuronal en utilisant la dérivée de la fonction d’activation.
La fonction sigmoïde
La fonction sigmoïde, caractérisée par une courbe en forme de S, est souvent considérée comme un cas particulier de la fonction logistique. Elle est surtout utile dans les cas où l’on doit prédire une probabilité en sortie.
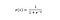
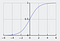
La fonction sigmoïde produit des valeurs comprises entre 0 et 1 (à juste titre si l’on considère qu’elle prédit des probabilités).
La dérivée sigmoïde
Cette brique fondamentale qui aide à former les réseaux neuronaux prend la forme :


Sans plus attendre, mettons-nous au travail sur la dérivation !
Approche 1

Approche 2 :
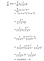
Pourquoi utilisons-nous cette version du dérivé ?
Dans l’étape de propagation avant, vous calculez la fonction sigmoïde (σ(x)) et avez sa valeur à portée de main. Tout en calculant la dérivée dans l’étape de rétropropagation, tout ce que vous avez à faire est de brancher la valeur de σ(x) dans la formule dérivée ci-dessus et voilà, vous êtes prêt à partir !
C’est tout les gars ! Merci d’avoir lu!