Dans cet article, découvrons les différents types de flip flops utilisés en électronique numérique.
Flop de base en électronique numérique
Cet article traite des circuits de base de flip flop comme le flip S-R, le flip J-K, le flip D et le flip T ainsi que les tables de vérité et leurs symboles de circuit correspondants.
Avant d’aborder le sujet, il est important que vous ayez connaissance de ses bases. Cliquez sur les liens ci-dessous pour plus d’informations.
PREUVE DE LA LOGIQUE BOOLEENNE
PREUVE DE LA LOGIQUE DES PORTES
PREUVE DE LA LOGIQUE DES ADDITEURS ET DES ADDITEURS COMPLETS
Les bascules sont en fait une application des portes logiques. Avec l’aide de la logique booléenne, vous pouvez créer une mémoire avec eux. Les bascules peuvent également être considérées comme l’idée la plus fondamentale d’une mémoire à accès aléatoire. Lorsqu’une certaine valeur d’entrée leur est donnée, elles sont mémorisées et exécutées, si les portes logiques sont conçues correctement. Une application plus élevée des flip flops est utile pour concevoir de meilleurs circuits électroniques.
L’application la plus couramment utilisée des flip flops est dans la mise en œuvre d’un circuit de rétroaction. Comme une mémoire repose sur le concept de rétroaction, les flip flops peuvent être utilisés pour la concevoir.
Il existe principalement quatre types de flip flops qui sont utilisés dans les circuits électroniques. Ils sont
- La basique Flip Flop ou S-R Flip Flop
- Delay Flip Flop
- J-K Flip Flop
- T Flip Flop
S-R Flip Flop
La flip flop SET-RESET est conçue à l’aide de deux portes NOR et aussi deux portes NAND. Ces bascules sont également appelées S-R Latch.
-
Bascule S-R utilisant une porte NOR
La conception d’une telle bascule comprend deux entrées, appelées le SET et le RESET . Il y a également deux sorties, Q et Q’. Le diagramme et la table de vérité sont présentés ci-dessous.
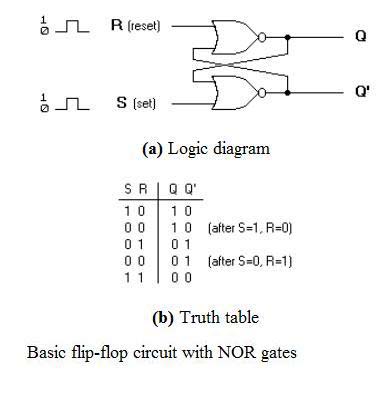
D’après le diagramme, il est évident que le flip flop a principalement quatre états. Ils sont
S=1, R=0-Q=1, Q’=0
Cet état est également appelé l’état SET.
S=0, R=1-Q=0, Q’=1
Cet état est connu comme l’état RESET.
Dans les deux états, vous pouvez voir que les sorties sont juste des compliments les unes des autres et que la valeur de Q suit la valeur de S.
S=0, R=0-Q & Q’ = Se souvenir
Si les deux valeurs de S et R sont commutées à 0, alors le circuit se souvient de la valeur de S et R dans leur état précédent.
S=1, R=1-Q=0, Q’=0
C’est un état invalide parce que les valeurs de Q et Q’ sont toutes deux 0. Elles sont censées être complémentaires l’une de l’autre. Normalement, cet état doit être évité.
-
Flop S-R utilisant une porte NAND
Le circuit du flip flop S-R utilisant une porte NAND et sa table de vérité sont présentés ci-dessous.
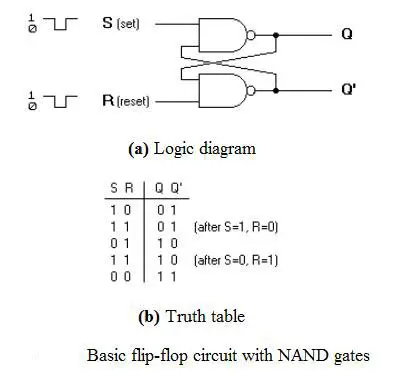
Comme le flip flop S-R de la porte NOR, celui-ci a également quatre états. Ils sont
S=1, R=0-Q=0, Q’=1
Cet état est également appelé l’état SET.
S=0, R=1-Q=1, Q’=0
Cet état est connu comme l’état RESET.
Dans les deux états, vous pouvez voir que les sorties sont juste des compléments les unes des autres et que la valeur de Q suit la valeur du complément de S.
S=0, R=0-Q=1, & Q’ =1
Si les deux valeurs de S et R sont commutées à 0, c’est un état invalide parce que les valeurs de Q et Q’ sont toutes deux à 1. Elles sont censées être complémentaires l’une de l’autre. Normalement, cet état doit être évité.
S=1, R=1-Q & Q’= Remember
Si les deux valeurs de S et R sont commutées à 1, alors le circuit se souvient de la valeur de S et R dans leur état précédent.
-
Flop S-R cadencé
Il est également appelé un flip flop S-R cadencé.
Les problèmes avec les flip flops S-R utilisant les portes NOR et NAND est l’état invalide. Ce problème peut être surmonté en utilisant une bascule SR bistable qui peut changer de sortie lorsque certains états invalides sont rencontrés, indépendamment de la condition des entrées Set ou Reset. Pour cela, une bascule S-R cadencée est conçue en ajoutant deux portes ET à une bascule NOR Gate de base. Le schéma du circuit et la table de vérité sont présentés ci-dessous.
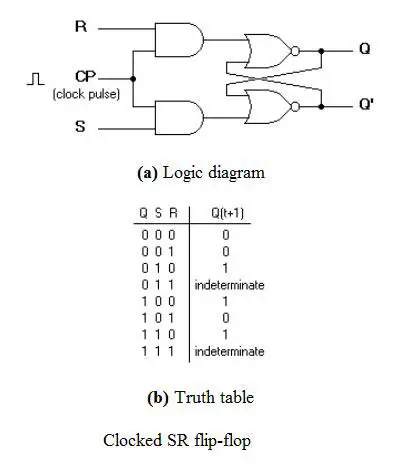
Une impulsion d’horloge est donnée aux entrées de la porte ET. Lorsque la valeur de l’impulsion d’horloge est ‘0’, les sorties des deux portes ET restent ‘0’. Dès qu’une impulsion est donnée, la valeur de CP devient ‘1’. Ceci fait que les valeurs de S et R passent par la bascule NOR Gate. Mais lorsque les valeurs de S et R passent à ‘1’, la valeur HIGH de CP les fait passer à ‘0’ pendant un court instant. Dès que l’impulsion est supprimée, l’état du flip flop devient intermédiaire. Ainsi, l’un ou l’autre des deux états peut être provoqué, et cela dépend si l’entrée d’activation ou de réinitialisation de la bascule reste à ‘1’ plus longtemps que la transition à ‘0’ à la fin de l’impulsion. Ainsi, les états invalides peuvent être éliminés.
Flop D
Le schéma de circuit et la table de vérité sont donnés ci-dessous.
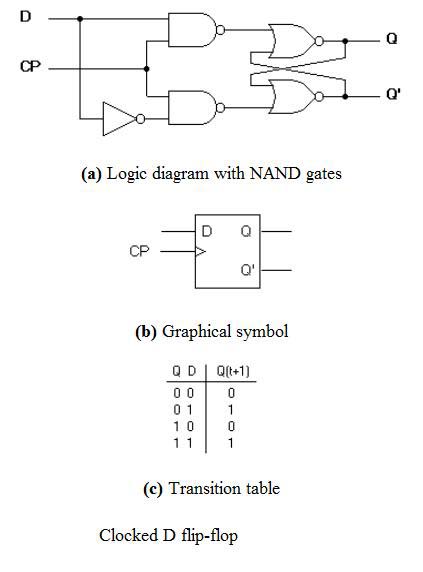
La bascule D est en fait une légère modification de la bascule SR cadencée expliquée ci-dessus. Sur la figure, vous pouvez voir que l’entrée D est connectée à l’entrée S et le complément de l’entrée D est connecté à l’entrée R. L’entrée D est transmise à la bascule lorsque la valeur de CP est ‘1’. Lorsque CP est HIGH, la bascule passe à l’état SET. Si elle est ‘0’, la bascule passe à l’état CLEAR.
Pour en savoir plus sur le déclenchement de la bascule, cliquez sur le lien ci-dessous.
TAOK : TRIGGERING OF FLIP FLOPS
TAOK : MASTER-SLAVE FLIP FLOP CIRCUIT
Flop J-K
Le schéma de circuit et la table de vérité d’un flip flop J-K sont présentés ci-dessous.
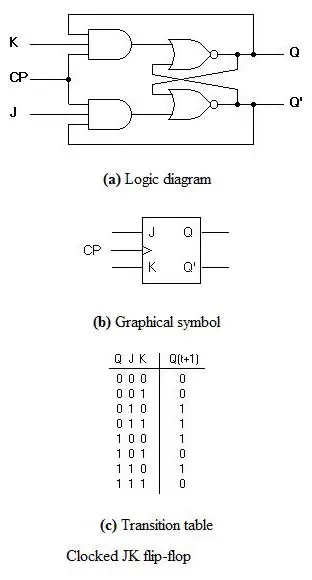
Une flip flop J-K peut également être définie comme une modification de la flip flop S-R. La seule différence est que l’état intermédiaire est plus raffiné et plus précis que celui d’une bascule S-R.
Le comportement des entrées J et K est le même que celui des entrées S et R de la bascule S-R. La lettre J signifie SET et la lettre K signifie CLEAR.
Lorsque les deux entrées J et K ont un état HIGH, la bascule passe à l’état complémentaire. Ainsi, pour une valeur de Q = 1, elle passe à Q=0 et pour une valeur de Q = 0, elle passe à Q=1.
Le circuit comprend deux portes ET à 3 entrées. La sortie Q de la bascule est renvoyée en rétroaction à l’entrée de l’ET avec d’autres entrées comme K et l’impulsion d’horloge . Ainsi, si la valeur de CP est ‘1’, la bascule reçoit un signal CLEAR, à condition que la valeur de Q ait été antérieure à 1. De même, la sortie Q’ de la bascule est donnée en retour à l’entrée de l’ET avec d’autres entrées comme J et l’impulsion d’horloge. Ainsi la sortie devient SET lorsque la valeur de CP est 1 seulement si la valeur de Q’ était plus tôt 1.
La sortie peut être répétée dans les transitions une fois qu’elles ont été complétées pour J=K=1 à cause de la connexion de rétroaction dans la bascule JK. Ceci peut être évité en fixant une durée inférieure au délai de propagation à travers la bascule. La restriction sur la largeur d’impulsion peut être éliminée avec une construction maître-esclave ou déclenchée par le front.
Flop T
C’est une version beaucoup plus simple de la flip-flop J-K. Les deux entrées J et K sont connectées ensemble et sont donc également appelées un flip flop J-K à une seule entrée. Lorsque l’on donne une impulsion d’horloge à la bascule, la sortie commence à basculer. Ici aussi, la restriction sur la largeur d’impulsion peut être éliminée avec une construction maître-esclave ou déclenchée par le front. Regardez le circuit et la table de vérité ci-dessous.
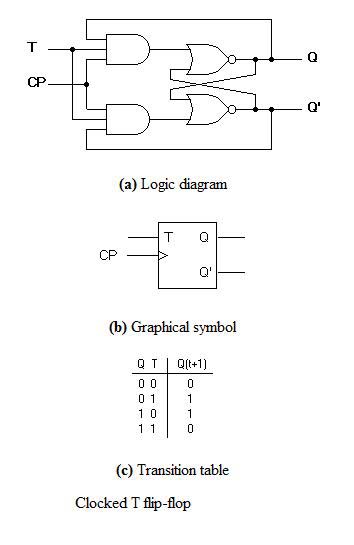
.