moins…
![]()
Il existe de nombreuses formules de ![]() de plusieurs types. Entre autres, il s’agit de séries, de produits, de constructions géométriques, de limites, de valeurs spéciales et d’itérations de pi.
de plusieurs types. Entre autres, il s’agit de séries, de produits, de constructions géométriques, de limites, de valeurs spéciales et d’itérations de pi.
![]() est intimement lié aux propriétés des cercles et des sphères. Pour un cercle de rayon
est intimement lié aux propriétés des cercles et des sphères. Pour un cercle de rayon ![]() , la circonférence et l’aire sont données par
, la circonférence et l’aire sont données par
|
(1)
|
|||
|
(2)
|
De même, pour une sphère de rayon ![]() , la surface et le volume enfermés sont
, la surface et le volume enfermés sont
|
(3)
|
|||
|
(4)
|
Une formule exacte de ![]() en termes de tangentes inverses de fractions unitaires est la formule de Machin
en termes de tangentes inverses de fractions unitaires est la formule de Machin
|
(5)
|
Il existe trois autres formules de type Machin, ainsi que des milliers d’autres formules similaires comportant plus de termes.
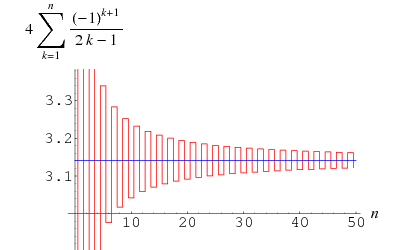
Gregory et Leibniz ont trouvé
|
(6)
|
|||
|
(7)
|
(Wells 1986, p. 50), qui est connue comme la série de Gregory et peut être obtenue en branchant ![]() dans la série de Leibniz pour
dans la série de Leibniz pour ![]() . L’erreur après le
. L’erreur après le ![]() e terme de cette série dans la série de Gregory est plus grande que
e terme de cette série dans la série de Gregory est plus grande que ![]() de sorte que cette somme converge si lentement que 300 termes ne suffisent pas à calculer
de sorte que cette somme converge si lentement que 300 termes ne suffisent pas à calculer ![]() correctement à deux décimales près ! Cependant, on peut la transformer en
correctement à deux décimales près ! Cependant, on peut la transformer en
|
(8)
|
où ![]() est la fonction zêta de Riemann (Vardi 1991, pp. 157-158 ; Flajolet et Vardi 1996), de sorte que l’erreur après
est la fonction zêta de Riemann (Vardi 1991, pp. 157-158 ; Flajolet et Vardi 1996), de sorte que l’erreur après ![]() termes est
termes est ![]() .
.
Une série à somme infinie à Abraham Sharp (ca. 1717) est donnée par
|
(9)
|
(Smith 1953, p. 311). Des séries simples supplémentaires dans lesquelles ![]() apparaît sont
apparaît sont
|
(10)
|
|||
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
|||
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
(Wells 1986, p. 53).
En 1666, Newton utilisa une construction géométrique pour dériver la formule
|
(18)
|
|||
|
(19)
|
qu’il a utilisé pour calculer ![]() (Wells 1986, p. 50 ; Borwein et al. 1989 ; Borwein et Bailey 2003, pp. 105-106). Les coefficients peuvent être trouvés à partir de l’intégrale
(Wells 1986, p. 50 ; Borwein et al. 1989 ; Borwein et Bailey 2003, pp. 105-106). Les coefficients peuvent être trouvés à partir de l’intégrale
|
(20)
|
|||
|
(21)
|
en prenant le développement en série de ![]() autour de 0, obtaining
autour de 0, obtaining
|
(22)
|
(OEIS A054387 et A054388). En utilisant la transformation d’amélioration de la convergence d’Euler, on obtient
|
(23)
|
|||
|
(24)
|
|||
|
(25)
|
(Beeler et al. 1972, point 120).
Cela correspond à brancher ![]() dans la série de puissance de la fonction hypergéométrique
dans la série de puissance de la fonction hypergéométrique ![]() ,
,
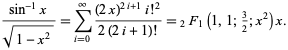 |
(26)
|
Malgré l’amélioration de la convergence, la série (◇) converge à un seul bit/terme. Au prix d’une racine carrée, Gosper a noté que ![]() donne 2 bits/terme,
donne 2 bits/terme,
|
(27)
|
et ![]() donne presque 3.39 bits/terme,
donne presque 3.39 bits/terme,
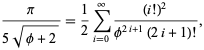 |
(28)
|
où ![]() est le nombre d’or. Gosper a également obtenu
est le nombre d’or. Gosper a également obtenu
|
(29)
|
Un algorithme à spigot pour ![]() est donné par Rabinowitz et Wagon (1995 ; Borwein et Bailey 2003, pp. 141-142).
est donné par Rabinowitz et Wagon (1995 ; Borwein et Bailey 2003, pp. 141-142).
Plus étonnamment encore, une expression sous forme fermée donnant un algorithme d’extraction de chiffres qui produit des chiffres de ![]() (ou
(ou ![]() ) en base 16 a été découverte par Bailey et al. (Bailey et al. 1997, Adamchik et Wagon 1997),
) en base 16 a été découverte par Bailey et al. (Bailey et al. 1997, Adamchik et Wagon 1997),
|
(30)
|
Cette formule, connue sous le nom de formule BBP, a été découverte en utilisant l’algorithme PSLQ (Ferguson et al. 1999) et est équivalente à
|
(31)
|
Il existe une série de formules de type BBP pour ![]() en puissances de
en puissances de ![]() , dont les premières formules indépendantes sont
, dont les premières formules indépendantes sont
|
(32)
|
|||
|
(33)
|
|||
| 4somme_(k=0)^(infty)(- 1)^k.1)^k |
(34)
|
||
 |
(35)
|
||
 |
(36)
|
||
 |
(37)
|
De même, il existe une série de formules de type BBP pour ![]() en puissances de
en puissances de ![]() , dont les premières formules indépendantes sont
, dont les premières formules indépendantes sont
|
(38)
|
|||
|
(39)
|
|||
 |
(40)
|
||
 |
(41)
|
||
 |
(42)
|
||
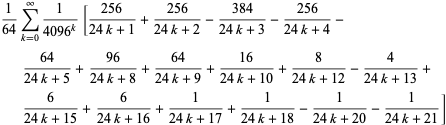 |
(43)
|
||
 |
(44)
|
||
 |
(45)
|
||
 |
(46)
|
||
 |
(47)
|
||
 |
(48)
|
F. Bellard a trouvé la formule BBP-type
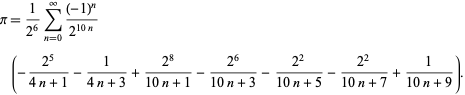 |
(49)
|
Une intégrale connexe est
|
(50)
|
(Dalzell 1944, 1971 ; Le Lionnais 1983, p. 22 ; Borwein, Bailey, et Girgensohn 2004, p. 3 ; Boros et Moll 2004, p. 125 ; Lucas 2005 ; Borwein et al. 2007, p. 14). Cette intégrale était connue par K. Mahler au milieu des années 1960 et apparaît dans un examen à l’Université de Sydney en novembre 1960 (Borwein, Bailey et Girgensohn, p. 3). Beukers (2000) et Boros et Moll (2004, p. 126) affirment qu’il n’est pas clair s’il existe un choix naturel de polynôme rationnel dont l’intégrale entre 0 et 1 produit ![]() , où 333/106 est le prochain convergent. Cependant, une intégrale existe pour le quatrième convergent, à savoir
, où 333/106 est le prochain convergent. Cependant, une intégrale existe pour le quatrième convergent, à savoir
|
(51)
|
(Lucas 2005 ; Bailey et al. 2007, p. 219). En fait, Lucas (2005) donne quelques autres intégrales de ce type.
Backhouse (1995) a utilisé l’identité
|
(52)
|
|||
|
(53)
|
|||
|
(54)
|
pour un entier positif ![]() et
et ![]() et où
et où ![]() ,
, ![]() , et
, et ![]() sont des constantes rationnelles pour générer un certain nombre de formules pour
sont des constantes rationnelles pour générer un certain nombre de formules pour ![]() . En particulier, si
. En particulier, si ![]() , alors
, alors ![]() (Lucas 2005).
(Lucas 2005).
Une formule similaire a été découverte par la suite par Ferguson, conduisant à un treillis bidimensionnel de telles formules qui peut être généré par ces deux formules données par
|
(55)
|
pour toute valeur complexe de ![]() (Adamchik et Wagon), donnant la formule BBP comme le cas particulier
(Adamchik et Wagon), donnant la formule BBP comme le cas particulier ![]() .
.
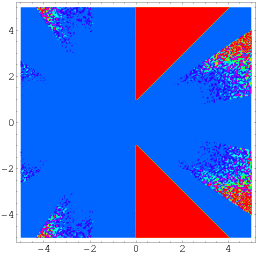
Une identité encore plus générale due à Wagon est donnée par
 |
(56)
|
(Borwein et Bailey 2003, p. 141), qui tient sur une région du plan complexe excluant deux portions triangulaires placées symétriquement autour de l’axe réel, comme illustré ci-dessus.
Une classe d’identités peut-être encore plus étrangement générale est donnée par
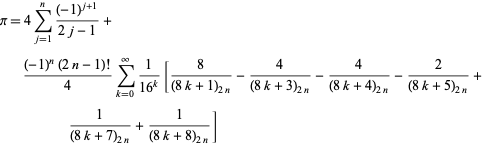 |
(57)
|
qui tient pour tout entier positif ![]() , où
, où ![]() est un symbole de Pochhammer (B. Cloitre, comm. pers, 23 janvier 2005). De façon encore plus étonnante, il existe une formule étroitement analogue pour le logarithme naturel de 2.
est un symbole de Pochhammer (B. Cloitre, comm. pers, 23 janvier 2005). De façon encore plus étonnante, il existe une formule étroitement analogue pour le logarithme naturel de 2.
A la suite de la découverte de la formule BBP à chiffres en base 16 et des formules connexes, des formules similaires dans d’autres bases ont été étudiées. Borwein, Bailey et Girgensohn (2004) ont récemment montré que ![]() n’a pas de formule arctangente BBP de type Machin qui ne soit pas binaire, bien que cela n’exclue pas un schéma complètement différent pour les algorithmes d’extraction de chiffres dans d’autres bases.
n’a pas de formule arctangente BBP de type Machin qui ne soit pas binaire, bien que cela n’exclue pas un schéma complètement différent pour les algorithmes d’extraction de chiffres dans d’autres bases.
S. Plouffe a conçu un algorithme pour calculer le ![]() e chiffre de
e chiffre de ![]() dans n’importe quelle base en
dans n’importe quelle base en ![]() étapes.
étapes.
Une ribambelle d’identités supplémentaires dues à Ramanujan, Catalan et Newton sont données par Castellanos (1988ab, pp. 86-88), dont plusieurs impliquant des sommes de nombres de Fibonacci. Ramanujan a trouvé
 |
(58)
|
(Hardy 1923, 1924, 1999, p. 7).
Plouffe (2006) a trouvé la belle formule
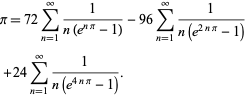 |
(59)
|
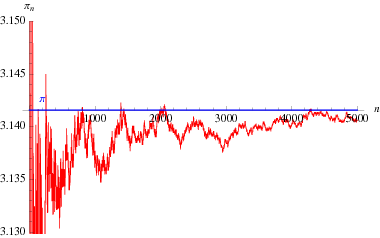
Une intéressante formule de produit infini due à Euler qui relie ![]() et le
et le ![]() e nombre premier
e nombre premier ![]() est
est
 |
(60)
|
||
|
(61)
|
(Blatner 1997, p. 119), tracée ci-dessus en fonction du nombre de termes dans le produit.
Une méthode similaire à celle d’Archimède peut être utilisée pour estimer ![]() en commençant par un
en commençant par un ![]() -gone et en reliant ensuite l’aire des
-gone et en reliant ensuite l’aire des ![]() -gones suivants. Soit
-gones suivants. Soit ![]() l’angle du centre d’un des segments du polygone,
l’angle du centre d’un des segments du polygone,
|
(62)
|
alors
|
(63)
|
(Beckmann 1989, pp. 92-94).
Vieta (1593) fut le premier à donner une expression exacte de ![]() en prenant
en prenant ![]() dans l’expression ci-dessus, ce qui donne
dans l’expression ci-dessus, ce qui donne
|
(64)
|
ce qui conduit à un produit infini de radicaux emboîtés,
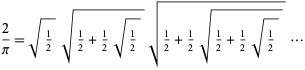 |
(65)
|
(Wells 1986, p. 50 ; Beckmann 1989, p. 95). Cependant, la convergence de cette expression n’a pas été rigoureusement prouvée avant Rudio en 1892.
Une formule connexe est donnée par
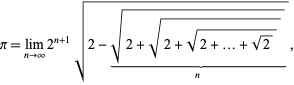 |
(66)
|
qui peut s’écrire
|
(67)
|
où ![]() est défini en utilisant l’itération
est défini en utilisant l’itération
 |
(68)
|
avec ![]() (J. Munkhammar, comm. pers, 27 avril 2000). La formule
(J. Munkhammar, comm. pers, 27 avril 2000). La formule
 |
(69)
|
est également étroitement liée.
Une jolie formule pour ![]() est donnée par
est donnée par
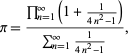 |
(70)
|
où le numérateur est une forme de la formule de Wallis pour ![]() et le dénominateur est une somme télescopique avec une somme 1/2 puisque
et le dénominateur est une somme télescopique avec une somme 1/2 puisque
|
(71)
|
(Sondow 1997).
Un cas particulier de la formule de Wallis donne
|
(72)
|
(Wells 1986, p. 50). Cette formule peut également être écrite
 |
(73)
|
où ![]() désigne un coefficient binomial et
désigne un coefficient binomial et ![]() est la fonction gamma (Knopp 1990). Euler a obtenu
est la fonction gamma (Knopp 1990). Euler a obtenu
|
(74)
|
ce qui découle de la valeur particulière de la fonction zêta de Riemann ![]() . Des formules similaires découlent de
. Des formules similaires découlent de ![]() pour tous les entiers positifs
pour tous les entiers positifs ![]() .
.
Une somme infinie due à Ramanujan est
|
(75)
|
(Borwein et al. 1989 ; Borwein et Bailey 2003, p. 109 ; Bailey et al.2007, p. 44). D’autres sommes sont données dans Ramanujan (1913-14),
|
(76)
|
et
|
(77)
|
|||
|
(78)
|
(Beeler et al. 1972, point 139 ; Borwein et al. 1989 ; Borwein et Bailey 2003, p. 108 ; Bailey et al. 2007, p. 44). L’équation (78) est dérivée d’une identité modulaire d’ordre 58, bien qu’une première dérivation n’ait pas été présentée avant Borwein et Borwein (1987). Les séries ci-dessus donnent toutes deux
|
(79)
|
(Wells 1986, p. 54) comme première approximation et fournissent, respectivement, environ 6 et 8 décimales par terme. De telles séries existent en raison de la rationalité de divers invariants modulaires.
La forme générale de la série est
|
(80)
|
où ![]() est un discriminant de forme quadratique binaire,
est un discriminant de forme quadratique binaire, ![]() est la fonction j,
est la fonction j,
|
(81)
|
|||
|
(82)
|
et les ![]() sont des séries d’Eisenstein. Un champ de nombre de classe
sont des séries d’Eisenstein. Un champ de nombre de classe ![]() implique des entiers algébriques de
implique des entiers algébriques de ![]() ème degré des constantes
ème degré des constantes ![]() ,
, ![]() , et
, et ![]() . De toutes les séries constituées uniquement de termes entiers, celle qui donne le plus de chiffres numériques dans le plus court laps de temps correspond au plus grand discriminant de classe numéro 1 de
. De toutes les séries constituées uniquement de termes entiers, celle qui donne le plus de chiffres numériques dans le plus court laps de temps correspond au plus grand discriminant de classe numéro 1 de ![]() et a été formulée par les frères Chudnovsky (1987). Le 163 apparaissant ici est le même que celui qui apparaît dans le fait que
et a été formulée par les frères Chudnovsky (1987). Le 163 apparaissant ici est le même que celui qui apparaît dans le fait que ![]() (la constante de Ramanujan) est très proche d’un nombre entier. De même, le facteur
(la constante de Ramanujan) est très proche d’un nombre entier. De même, le facteur ![]() provient de l’identité de la fonction j pour
provient de l’identité de la fonction j pour ![]() . La série est donnée par
. La série est donnée par
|
(83)
|
|||
|
(84)
|
(Borwein et Borwein 1993 ; Beck et Trott ; Bailey et al. 2007, p. 44). Cette série donne 14 chiffres précis par terme. La même équation sous une autre forme a été donnée par les frères Chudnovsky (1987) et est utilisée par le langage Wolfram pour calculer ![]() (Vardi 1991 ; Wolfram Research),
(Vardi 1991 ; Wolfram Research),
|
(85)
|
où
|
(86)
|
|||
|
(87)
|
|||
|
(88)
|
La meilleure formule pour la classe numéro 2 (plus grand discriminant ![]() ) est
) est
|
(89)
|
où
|
(90)
|
|||
|
(91)
|
|||
|
(92)
|
(Borwein et Borwein 1993). Cette série ajoute environ 25 chiffres pour chaque terme supplémentaire. La série qui converge le plus rapidement pour la classe numéro 3 correspond à ![]() et donne 37-38 chiffres par terme. La série de la classe numéro 4 qui converge le plus rapidement correspond à
et donne 37-38 chiffres par terme. La série de la classe numéro 4 qui converge le plus rapidement correspond à ![]() et est
et est
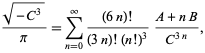 |
(93)
|
où
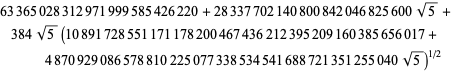 |
(94)
|
||
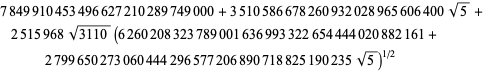 |
(95)
|
||
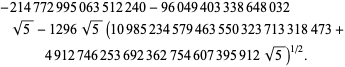 |
(96)
|
Cela donne 50 chiffres par terme. Borwein et Borwein (1993) ont développé un algorithme général pour générer de telles séries pour un nombre de classe arbitraire.
Une liste complète des séries de Ramanujan pour ![]() trouvées dans ses deuxième et troisième carnets est donnée par Berndt (1994, pp. 352-354),
trouvées dans ses deuxième et troisième carnets est donnée par Berndt (1994, pp. 352-354),
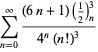 |
(97)
|
||
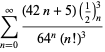 |
(98)
|
||
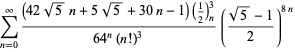 |
(99)
|
||
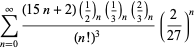 |
(100)
|
||
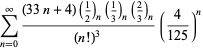 |
(101)
|
||
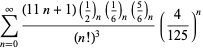 |
(102)
|
||
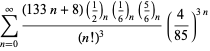 |
(103)
|
||
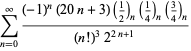 |
(104)
|
||
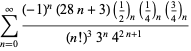 |
(105)
|
||
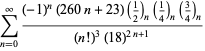 |
(106)
|
||
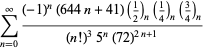 |
(107)
|
||
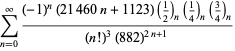 |
(108)
|
||
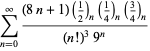 |
(109)
|
||
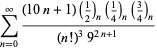 |
(110)
|
||
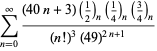 |
(111)
|
||
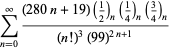 |
(112)
|
||
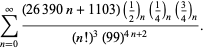 |
(113)
|
Ces équations ont été prouvées pour la première fois par Borwein et Borwein (1987a, pp. 177-187). Borwein et Borwein (1987b, 1988, 1993) ont prouvé d’autres équations de ce type, et Chudnovsky et Chudnovsky (1987) ont trouvé des équations similaires pour d’autres constantes transcendantales (Bailey et al. 2007, pp. 44-45).
Une liste complète des équations indépendantes connues de ce type est donnée par
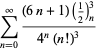 |
(114)
|
||
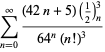 |
(115)
|
||
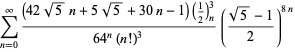 |
(116)
|
||
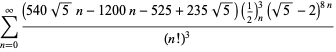 |
(117)
|
||
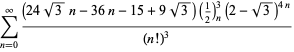 |
(118)
|
pour ![]() avec des signes non alternatifs,
avec des signes non alternatifs,
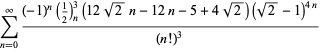 |
(119)
|
||
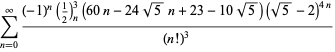 |
(120)
|
||
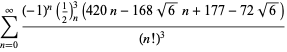 |
(121)
|
||
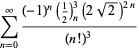 |
(122)
|
pour ![]() avec des signes alternés,
avec des signes alternés,
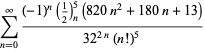 |
(123)
|
||
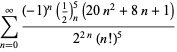 |
(124)
|
pour ![]() (Guillera 2002, 2003, 2006),
(Guillera 2002, 2003, 2006),
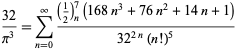 |
(125)
|
pour ![]() (Guillera 2002, 2003, 2006), et aucune autre pour
(Guillera 2002, 2003, 2006), et aucune autre pour ![]() n’est connue (Bailey et al. 2007, pp. 45-48).
n’est connue (Bailey et al. 2007, pp. 45-48).
Bellard donne la formule exotique
 |
(126)
|
where
|
(127)
|
Gasper cite le résultat
|
(128)
|
où ![]() est une fonction hypergéométrique généralisée, et le transforme en
est une fonction hypergéométrique généralisée, et le transforme en
|
(129)
|
Un résultat fascinant dû à Gosper est donné par
|
(130)
|
![]() satisfait l’inégalité
satisfait l’inégalité
|
(131)
|
D. Terr (comm. pers.) a noté la curieuse identité
|
(132)
|
impliquant les 9 premiers chiffres de pi.