Le contrôle proportionnel n’est qu’une façon de réagir à une erreur dans le système. Le problème de la commande proportionnelle est qu’elle ne peut pas détecter les tendances et s’y adapter. C’est le travail de la commande intégrale.
Il y a un autre exemple de graphique de l’erreur dans un système en fonction du temps à gauche de la figure 6. Là encore, il peut s’agir de la distance d’un robot par rapport à un objet, ou du niveau de fluide dans un réservoir, ou de la température dans un four d’usine. Peut-être que la cible que le robot suit continue de s’éloigner du robot à une vitesse que le robot ne peut pas rattraper. Peut-être que le joint de la porte du four est usé ; peut-être que le prélèvement de liquide dans le réservoir est anormalement élevé. Quelle que soit la cause, le système proportionnel n’étant pas conçu pour réagir aux tendances, il ne peut pas détecter et corriger le problème. C’est là que la commande intégrale entre en jeu.
L’intégrale mesure la zone entre les valeurs d’erreur et l’axe du temps. Si l’erreur ne revient pas à zéro, la zone de l’erreur devient de plus en plus grande. La partie droite de la figure 6 montre comment la sortie intégrale peut réagir à ce type de tendance. Lorsque la zone entre la courbe d’erreur et l’axe du temps augmente, la sortie augmente proportionnellement à cette zone. Par conséquent, la sortie entraîne l’actionneur de plus en plus fort pour corriger l’erreur.
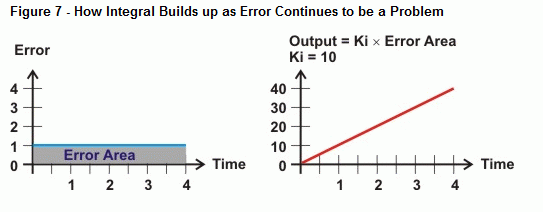
Alors, que se passe-t-il lorsque l’erreur n’est pas une ligne droite, comme la courbe illustrée à la figure 8 ? C’est ce que détermine l’opération de calcul de l’intégration, l’aire entre une courbe et un axe. Dans le cas de la commande intégrale, plus le temps passe avec une erreur, plus l’aire sous la courbe augmente, tout comme la valeur que le calcul intégral utilisera pour lutter contre l’erreur du système. Si la courbe d’erreur passe en dessous de l’axe du temps, l’accumulation de la zone négative se soustrait à l’accumulation de la zone positive. Lorsqu’elle est réglée correctement, la commande intégrale peut aider le système à se concentrer sur une erreur de zéro.
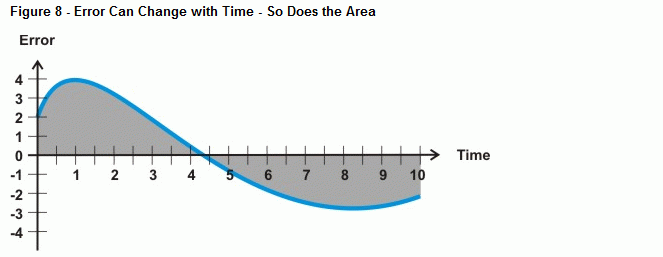
Le BASIC Stamp peut approximer l’erreur sous la courbe avec une intégration numérique. La figure 9 montre comment vous pouvez approximer l’erreur sous une courbe en additionnant l’aire d’un tas de petits rectangles entre la courbe d’erreur et l’axe du temps. La surface de chaque case correspond à l’erreur multipliée par le temps entre les mesures. En additionnant toutes les aires des boîtes, vous obtenez une approximation de l’aire sous la courbe.
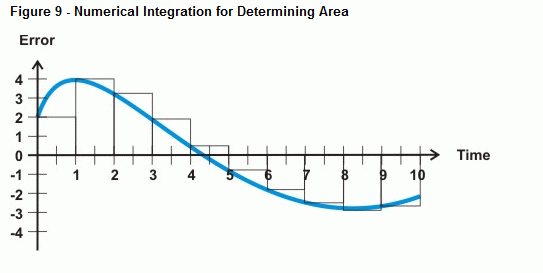
Si vos mesures sont uniformément espacées, vous pouvez appeler la largeur de chaque boîte une valeur de 1. Cela rend les mathématiques beaucoup plus simples que d’essayer de tenir compte de 20 ms entre les échantillons, 5 minutes entre les échantillons, ou quel que soit votre taux d’échantillonnage qui s’avère être. Au lieu de multiplier l’erreur par l’incrément de temps entre les échantillons, puis de l’ajouter à l’erreur suivante multipliée par le temps, vous pouvez simplement multiplier chaque échantillon d’erreur par un temps de 1. Le résultat est que vous pouvez simplement garder un total courant de mesures d’erreur pour votre calcul intégral. Voici un exemple de comment faire cela avec PBASIC:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
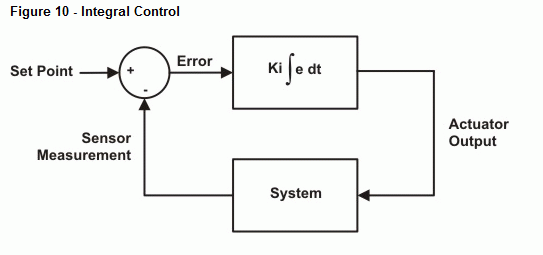
Le programme de l’exemple suivant effectue une intégration numérique sur le signal d’erreur et ajuste la sortie en conséquence. Comme pour le contrôle proportionnel, il existe une constante qui met à l’échelle la sortie d’intégration à la valeur désirée. Par souci de simplicité, nous utiliserons à nouveau 10 pour Ki. La figure 10 présente un schéma fonctionnel de la boucle de régulation. Le terme Kp ∫ edt fait référence à Kp multiplié par l’intégrale de l’erreur dans le temps. En d’autres termes, Kp multiplié par la zone accumulée entre la courbe d’erreur et l’axe du temps.
Programme d’exemple – IntegralAlgorithm.bs2
- Entrez, enregistrez et exécutez IntegralAlgorithm.bs2.
- Entrez cette séquence de valeurs dans le volet de fenêtre d’émission du terminal de débogage : 3 3 3 3 3 3 3 3 3. Remarquez comment la sortie de l’intégrale devient plus grande à chaque fois que le 3 est répété. C’est le travail de l’intégrale, détecter les tendances et augmenter l’entraînement pour le corriger si nécessaire.
- Essayez maintenant cette séquence : 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. L’aire sous cette courbe est 0 puisque l’aire négative est la même que l’aire positive. C’est également ce à quoi le calcul intégral arrivera lorsque vous aurez fini de saisir la séquence.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Comment fonctionne IntegralAlgorithm.bs2
Ce programme est un ProportionalAlgorithm.bs2 modifié pour effectuer le calcul intégral à la place. Il y a maintenant deux types différents d’erreurs à suivre, donc là le tableau de variables d’erreur a été étendu à deux éléments. La variable error(0) suit l’erreur actuelle, et error(1) suit l’erreur accumulée. Les constantes Current CON 0 et Accumulator CON 1 rendent la comptabilité un peu plus sensée avec error(current) et error(accumulator).
L’autre changement qui a été fait est que l’erreur est accumulée et que la sortie intégrale est calculée avec ces deux déclarations :
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Votre tour – Bridage de la sortie intégrale
Comme vous l’avez peut-être compris en entrant à plusieurs reprises 3 dans le terminal de débogage, la sortie intégrale du variateur peut vraiment commencer à s’emballer. Vous pouvez utiliser les opérateurs MIN et MAX pour empêcher le contrôle intégral de déborder sur la sortie. Répétons l’activité de décalage du servo et limitons la sortie de 650 à 850.
- Changez l’instruction drive = i en drive = i + Offset MIN 650 MAX 850.
- Exécutez le programme et vérifiez que la sortie intégrale est limitée à des valeurs comprises entre 650 et 850. Essayez d’entrer 2 à plusieurs reprises, puis -2 à plusieurs reprises.
.