Comment se préparer aux questions de géométrie d’un test de mathématiques
Informations générales
La géométrie est juste un nom fantaisiste pour l’étude des lignes et des formes. Il existe certainement d’autres principes et sujets difficiles, mais nous avons ici les bases. Vous devrez les maîtriser avant d’aborder des concepts plus avancés.
(Veuillez noter que si une figure est étiquetée « exemple » dans ce guide, il se peut qu’elle ne soit pas la seule représentation de cette figure, mais qu’elle en soit une.)
Points et lignes
Un point en géométrie est un emplacement. Il n’a ni longueur, ni largeur, ni profondeur. On utilise un point et une majuscule pour représenter un point.
Un segment de ligne est défini par deux points et tous les points entre eux. Les deux points sont appelés points d’extrémité du segment. Un segment a une seule dimension : la longueur. Pour écrire un segment, on place une barre sur les deux points d’extrémité. \(\overline{AB}\) ou \(\overline{BA}\) est ce segment:

Une ligne s’étend dans les deux sens sans fin. Pour écrire une ligne, placez une barre avec deux flèches sur deux points quelconques de la ligne. \(\overleftrightarrow{AB}\) ou \(\overleftrightarrow{BA}\) est la ligne:

Un rayon commence à un point d’extrémité et s’étend sans fin dans une seule direction. Pour écrire une raie, placez une barre avec une flèche pointant vers la droite sur deux points : le point d’extrémité et tout autre point (dans cette direction). \(\N-overrightarrow{AB}\) est le rayon:

Note : vous ne pouvez pas écrire un rayon avec la flèche pointant vers la gauche comme \(\N-overleftarrow{BA}\). De plus, l’ordre est important. \(\overrightarrow{BA}\) n’est pas la même chose que \(\overrightarrow{AB}\). La première lettre est toujours le point de départ d’un rayon.
Deux lignes, segments ou rayons sont perpendiculaires s’ils forment un angle droit (voir ci-dessous). Utilisez le symbole \(\perp\) pour indiquer la perpendicularité. Par exemple, si \(\overline{AB}\) est perpendiculaire à \(\overline{CD}\), vous pouvez écrire \(\overline{AB} \perp \overline{CD}\).
Exemples : 
Deux lignes sont parallèles si elles ne se croisent jamais. Si \(\overleftrightarrow{AB}\) est parallèle à \(\overleftrightarrow{CD}\), on peut écrire \(\overleftrightarrow{AB} \parallel \overleftrightarrow{CD}\).
Exemples : 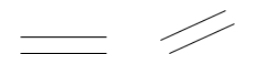
Formes planes
En géométrie, un plan est une surface plane à deux dimensions qui s’étend à l’infini. Ces deux dimensions sont la longueur et la largeur. Ainsi, les formes planes sont des formes « plates », comme les carrés, les cercles et les triangles.
Formes communes
Un polygone est une surface fermée sur un plan délimitée par des segments de droite appelés côtés.
Exemples : 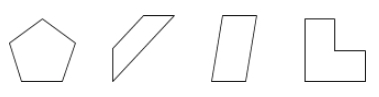
Un polygone régulier est un polygone dont tous les segments et les angles intérieurs sont congrus.
Exemples:
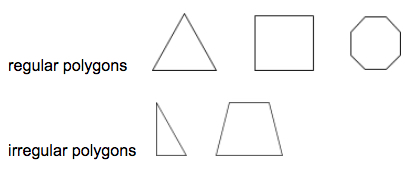
Un triangle est un polygone à trois côtés.
Exemples:
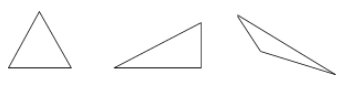
Quadrilatères – polygones à quatre côtés
Un parallélogramme est un type de quadrilatère dont les côtés opposés sont parallèles et congruents. Les angles opposés d’un parallélogramme sont également congruents.
Exemples : 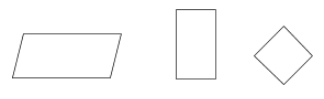
Un rectangle est un parallélogramme avec quatre angles droits.
Exemples : 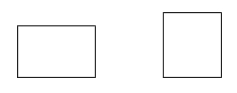
Un rhombe est un parallélogramme dont les quatre côtés sont congrus.
Exemples : 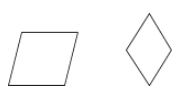
Un carré est un parallélogramme qui est à la fois un losange et un rectangle (tous les côtés sont congrus et tous les angles sont droits).
Exemples : 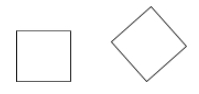
Un trapèze est un quadrilatère qui n’a qu’une paire de côtés parallèles.
Exemples : 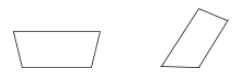
Polygones à plus de quatre côtés
\
\(^1\) Un polygone à 11 côtés peut aussi être appelé un endécagone ou un undécagone.
Mesurer les formes
Le périmètre est la distance totale autour d’un polygone. Pour trouver le périmètre, il suffit d’additionner les longueurs de tous les côtés. Si le polygone est régulier (tous les côtés sont congruents) et que la longueur d’un côté est \(s\), multipliez alors le nombre de côtés par \(s\) pour trouver le périmètre. Par exemple, le périmètre d’un pentagone régulier est de \(P_\text{reg pentagon}=5s\)
.