Qu’est-ce que Python SciPy et comment l’utiliser ?

Les mathématiques traitent d’un nombre énorme de concepts très importants mais en même temps, complexes et chronophages. Cependant, Python fournit la bibliothèque SciPy à part entière qui résout ce problème pour nous. Dans ce tutoriel SciPy, vous apprendrez à utiliser cette bibliothèque ainsi que quelques fonctions et leurs exemples.

Avant de poursuivre, jetez un œil à tous les sujets abordés dans cet article :

• Qu’est-ce que SciPy ?
• NumPy vs SciPy
• Sous-packages dans SciPy
• Fonctions de base
• Fonctions spéciales
• Fonctions d’intégration
• Fonctions d’optimisation
• Fonctions de transformation de Fourier
• Fonctions de traitement du signal. Processing Functions
• Linear Algebra
• Sparse Eigenvalues
• Spatial Data Structures and Algorithms
• Multidimensional Image Processing Functions
• File IO

So let’s started. 🙂

SciPy est une bibliothèque Python open-source qui est utilisée pour résoudre des problèmes scientifiques et mathématiques. Elle est construite sur l’extension NumPy et permet à l’utilisateur de manipuler et de visualiser des données avec un large éventail de commandes de haut niveau. Comme mentionné précédemment, SciPy s’appuie sur NumPy et donc si vous importez SciPy, il n’est pas nécessaire d’importer NumPy.

NumPy vs SciPy

Les deux bibliothèques NumPy et SciPy sont des bibliothèques Python utilisées pour l’analyse mathématique et numérique. NumPy contient des données de tableau et des opérations de base telles que le tri, l’indexation, etc tandis que, SciPy se compose de tout le code numérique. Bien que NumPy fournisse un certain nombre de fonctions qui peuvent aider à résoudre les problèmes d’algèbre linéaire, de transformées de Fourier, etc., SciPy est la bibliothèque qui contient en fait des versions complètes de ces fonctions ainsi que de nombreuses autres. Cependant, si vous faites de l’analyse scientifique en utilisant Python, vous devrez installer à la fois NumPy et SciPy puisque SciPy se construit sur NumPy.

Sous-paquets dans SciPy:

SciPy a un certain nombre de sous-paquets pour divers calculs scientifiques qui sont présentés dans le tableau suivant:

Cependant, pour une description détaillée, vous pouvez suivre la documentation officielle.

Ces paquets doivent être importés exclusivement avant de les utiliser. Par exemple :

from scipy import cluster

Avant d’examiner chacune de ces fonctions en détail, jetons d’abord un coup d’œil aux fonctions qui sont communes à la fois à NumPy et à SciPy.

Interaction avec NumPy :

SciPy s’appuie sur NumPy et vous pouvez donc faire usage des fonctions de NumPy lui-même pour manipuler les tableaux. Pour connaître en profondeur ces fonctions, vous pouvez simplement faire usage des fonctions help(), info() ou source().

help():

Pour obtenir des informations sur une fonction quelconque, vous pouvez faire usage de la fonction help(). Cette fonction peut être utilisée de deux manières :

• sans aucun paramètre
• en utilisant des paramètres

Voici un exemple qui montre les deux méthodes ci-dessus :

from scipy import cluster 
help(cluster) #with parameter 
help() #without parameter

Lorsque vous exécutez le code ci-dessus, la première help() renvoie les informations sur le sous-module cluster. La seconde help() demande à l’utilisateur d’entrer le nom de n’importe quel module, mot-clé, etc. pour lequel l’utilisateur désire chercher des informations. Pour arrêter l’exécution de cette fonction, il suffit de taper ‘quit’ et d’appuyer sur entrée.

info():

Cette fonction renvoie des informations sur les fonctions, les modules, etc…

scipy.info(cluster)

source():

Le code source est renvoyé uniquement pour les objets écrits en Python. Cette fonction ne renvoie pas d’informations utiles dans le cas où les méthodes ou les objets sont écrits dans un autre langage comme le C. Cependant dans le cas où vous voulez faire usage de cette fonction, vous pouvez le faire comme suit :

scipy.source(cluster)

Fonctions spéciales:

SciPy fournit un certain nombre de fonctions spéciales qui sont utilisées en physique mathématique comme les fonctions elliptiques, les fonctions de commodité, gamma, bêta, etc. Pour rechercher toutes les fonctions, vous pouvez faire usage de la fonction help() comme décrit précédemment.

Fonctions exponentielles et trigonométriques:

Le paquet de fonctions spéciales de SciPy fournit un certain nombre de fonctions grâce auxquelles vous pouvez trouver des exposants et résoudre des problèmes trigonométriques.

Considérez l’exemple suivant:

EXEMPLE:

from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)

SORTIE:

1000,0
8,0
1,0
0.7071067811865475

Il existe de nombreuses autres fonctions présentes dans le paquet de fonctions spéciales de SciPy que vous pouvez essayer par vous-même.

Fonctions d’intégration:

SciPy fournit un certain nombre de fonctions pour résoudre les intégrales. Allant de l’intégrateur différentiel ordinaire à l’utilisation des règles trapézoïdales pour calculer les intégrales, SciPy est un entrepôt de fonctions pour résoudre tous les types de problèmes d’intégrales.

Intégration générale:

SiPy fournit une fonction nommée quad pour calculer l’intégrale d’une fonction qui a une variable. Les limites peuvent être ( ) pour indiquer des limites infinies. La syntaxe de la fonction quad() est la suivante:

SYNTAX:

quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)

Ici, la fonction sera intégrée entre les limites a et b (peut aussi être infinie).

EXEMPLE:

from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)

Dans l’exemple ci-dessus, la fonction ‘a’ est évaluée entre les limites 0, 1. Lorsque ce code est exécuté, vous verrez la sortie suivante.

Sortie:

(3,9086503371292665, 4,3394735994897923e-14)

Fonction intégrale double:

SciPy fournit dblquad qui peut être utilisé pour calculer des intégrales doubles. Une intégrale double, comme beaucoup d’entre nous le savent, est constituée de deux variables réelles. La fonction dblquad() prendra comme paramètre la fonction à intégrer ainsi que 4 autres variables qui définissent les limites et les fonctions dy et dx.

EXEMPLE:

from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)

OUTPUT:

-1.33333333333335, 1,4802973661668755e-14)

SciPy fournit diverses autres fonctions pour évaluer les intégrales triples, les intégrales n, les intégrales de Romberg, etc que vous pouvez explorer plus en détail. Pour trouver tous les détails sur les fonctions requises, utilisez la fonction d’aide.

Fonctions d’optimisation:

La scipy.optimize fournit un certain nombre d’algorithmes d’optimisation couramment utilisés qui peuvent être vus en utilisant la fonction d’aide.

Il se compose essentiellement des éléments suivants :

• Minimisation sans contrainte et contrainte de fonctions scalaires multivariées c’est-à-dire minimiser (par exemple BFGS, Newton Conjugate Gradient, Nelder_mead simplex, etc)
• Routines d’optimisation globale (par exemple. differential_evolution, dual_annealing, etc)
• Minimisation des moindres carrés et ajustement de courbe (eg. least_squares, curve_fit, etc)
• Minimiseurs de fonctions univariées scalaires et trouveurs de racines (eg. minimize_scalaire et root_scalaire)
• Solveurs de systèmes d’équations multivariées utilisant des algorithmes tels que Powell hybride, Levenberg-Marquardt.

Fonction Rosenbrook:

La fonction Rosenbrook ( rosen) est un problème de test utilisé pour les algorithmes d’optimisation basés sur le gradient. Elle est définie comme suit dans SciPy:

EXEMPLE:

import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)

OUTPUT : 7371.0399999999945

Nelder-Mead:

La méthode de Nelder-Mead est une méthode numérique souvent utilisée pour trouver le min/max d’une fonction dans un espace multidimensionnel. Dans l’exemple suivant, la méthode de minimisation est utilisée avec l’algorithme de Nelder-Mead.

EXEMPLE:

from scipy import optimize
a = 
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x

OUTPUT : array()

Fonctions d’interpolation:

Dans le domaine de l’analyse numérique, l’interpolation fait référence à la construction de nouveaux points de données dans un ensemble de points de données connus. La bibliothèque SciPy est constituée d’un sous-paquetage nommé scipy.interpolate qui comprend des fonctions et des classes de splines, des classes d’interpolation unidimensionnelles et multidimensionnelles (univariées et multivariées), etc.

Interpolation univariée:

L’interpolation univariée est fondamentalement un domaine d’ajustement de courbe qui trouve la courbe qui fournit un ajustement exact à une série de points de données bidimensionnels. SciPy fournit la fonction interp1d qui peut être utilisée pour produire une interpolation univariée.

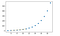
EXEMPLE:

import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()

OUTPUT:

Interpolation multivariée:

L’interpolation multivariée (interpolation spatiale ) est une sorte d’interpolation sur des fonctions qui consistent en plus d’une variable. L’exemple suivant démontre un exemple de la
Interpolation sur une grille 2-D en utilisant la fonction interp2d(x, y, z) basiquement utilisera des tableaux x, y, z pour approximer une certaine fonction interp2d. f : « z = f(x, y) » et retourne une fonction dont la méthode d’appel utilise l’interpolation spline pour trouver la valeur des nouveaux points.
EXEMPLE:

from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()

OUTPUT:

Fonctions de transformation de Fourier:

L’analyse de Fourier est une méthode qui traite de l’expression d’une fonction comme une somme de composantes périodiques et de la récupération du signal à partir de ces composantes. Les fonctions fft peuvent être utilisées pour retourner la transformée de Fourier discrète d’une séquence réelle ou complexe.

EXEMPLE:

from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)

SORTIE :

De même, vous pouvez trouver l’inverse de celle-ci en utilisant la fonction ifft comme suit :

EXEMPLE:

rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)

SORTIE :

Fonctions de traitement du signal:

Le traitement du signal traite de l’analyse, de la modification et de la synthèse de signaux tels que le son, les images, etc. SciPy fournit certaines fonctions à l’aide desquelles vous pouvez concevoir, filtrer et interpoler des données unidimensionnelles et bidimensionnelles.

Filtrage:

En filtrant un signal, vous en retirez essentiellement les composants indésirables. Pour effectuer un filtrage ordonné, vous pouvez faire appel à la fonction order_filter. Cette fonction effectue essentiellement un filtrage ordonné sur un tableau. La syntaxe de cette fonction est la suivante :

SYNTAX :

filtre_ordonné(a, domaine, rang)

a = tableau d’entrée à N dimensions

domaine = tableau de masque ayant le même nombre de dimensions que `a`

rang = nombre non négatif qui sélectionne les éléments de la liste après qu’elle ait été triée (0 est le plus petit suivi de 1…)

EXEMPLE :

from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))

OUTPUT:

]

]

Waveforms:

Le scipy.signal est également constitué de diverses fonctions qui peuvent être utilisées pour générer des formes d’onde. Une de ces fonctions est la fonction chirp. Cette fonction est un générateur de cosinus balayé en fréquence et la syntaxe est la suivante :

SYNTAX :
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)

où,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()

import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)

import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)

from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)

import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()

import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)

import scipy.io as sio