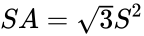Pour la revue académique, voir Tetrahedron (revue).
| Tétraèdre régulier | |
|---|---|
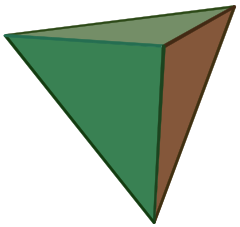 (Cliquez ici pour le modèle tournant) |
|
| Type | Solide platonique |
| Eléments | F = 4, E = 6 V = 4 (χ = 2) |
| Faces par côtés | 4{3} |
| Schläfli symbole | {3,3} et s{2,2} |
| Symbole de Wythoff | 3 | 2 3 | 2 2 2 |
| Anneau de Coxeter-Dynkin | |
| Symmétrie | Td ou (*332) |
| U01, C15, W1 | |
| Propriétés | Deltaèdre convexe régulier |
| Angle dièdre | 70.528779° = arccos(1/3) |
 3.3.3 (figure à sommets) |
 Self-dual (polyèdre dual) |
 Net |
|
Un tétraèdre (pluriel : tétraèdre) est un polyèdre composé de quatre faces triangulaires, dont trois se rencontrent à chaque sommet. Un tétraèdre régulier est un tétraèdre dans lequel les quatre triangles sont réguliers, ou « équilatéraux », et est l’un des solides de Platon.
Le tétraèdre est une sorte de pyramide, qui est un polyèdre avec une base polygonale plate et des faces triangulaires reliant la base à un point commun. Dans le cas d’un tétraèdre, la base est un triangle (n’importe laquelle des quatre faces peut être considérée comme la base), c’est pourquoi un tétraèdre est également connu sous le nom de pyramide triangulaire ou de deltaèdre digonal.
Formules du tétraèdre régulier
Le volume est
La surface est
Template :Commonscat
- F. M. Jackson et Weisstein, Eric W., « Tetrahedron » de MathWorld.
- Weisstein, Eric W., « Tetrahedron » de MathWorld.
- Weisstein, Eric W., « Tetrahedron » de MathWorld.
- Le polyèdre uniforme
- Tétraèdre : Modèle interactif de polyèdres
- K. J. M. MacLean, Une analyse géométrique des cinq solides de Platon et d’autres polyèdres semi-réguliers
- La formule de Piero della Francesca pour le volume du tétraèdre à MathPages
- Modèles gratuits en papier d’un tétraèdre et de nombreux autres polyèdres
- Un étonnant , Space Filling, Non-regular Tetrahedron qui comprend également une description d’un « anneau rotatif de tétraèdres », également connu sous le nom de kaléidocycle.
- Réseau central tétraédrique Application d’une structure tétraédrique pour créer un réseau de données résilient à mailles partielles
- Formules exactes explicites pour le tenseur d’inertie d’un tétraèdre arbitraire en fonction de ses coordonnées de sommet
- Le tenseur d’inertie d’un tétraèdre
.