Introduction
Les transformations de coordonnées sont assez peu intuitives en 2D, et positivement pénibles en 3D. Cette page les aborde dans l’ordre suivant : (i) vecteurs en 2-D, (ii) tenseurs en 2-D, (iii) vecteurs en 3-D, (iv) tenseurs en 3-D, et enfin(v) transformations tensorielles de 4ème rang.
Un aspect majeur des transformations de coordonnées est l’évaluation de la matrice de transformation,surtout en 3-D. Ceci est abordé ici, et discuté en détail à la page suivante.
Il est très important de reconnaître que toutes les transformations de coordonnées sur cette page sont des rotations du système de coordonnées alors que l’objet lui-même reste fixe. L' »objet » peut être un vecteur comme la force ou la vitesse, ou un tenseur comme la contrainte ou la déformation d’un composant. Les rotations d’objets sont abordées dans les sections ultérieures.
Transformations de coordonnées 2D de vecteurs
La pomme de terre académique fournit un excellent exemple de la façon dont les transformations de coordonnées s’appliquent aux vecteurs, tout en soulignant que c’est le système de coordonnées qui tourne et non le vecteur… ou la pomme de terre.
La pomme de terre à gauche porte un vecteur. Mais sans système de coordonnées, il n’y a aucun moyen de décrire le vecteur.On a donc ajouté un système de coordonnées à la pomme de terre comme indiqué sur la droite, ce qui permet de décrire le vecteur maintenant comme \({\bf v} = 2{\bf i} + 9{\bf j}\).

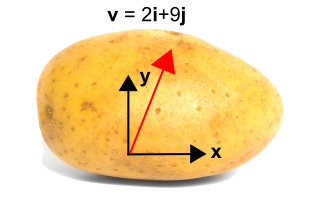
Nous introduisons maintenant un système de coordonnées pivoté, représenté en bleu ci-dessous, en utilisant \(x’\) et \(y’\). Le nouveau système est tourné dans le sens inverse des aiguilles d’une montre d’un angle, \(\theta\), par rapport au système de coordonnées initial. Notez que le vecteur lui-même ne change pas du tout. C’est toujours le même vecteur que précédemment. Mais il est décrit par des valeurs numériques différentes dans le nouveau système de coordonnées. Dans ce cas, le vecteur est plus étroitement parallèle au nouvel axe \(x’\) qu’à l’axe \(y’\), donc la composante \({\bf i’}\) sera plus grande que la composante \({\bf j’}\). La transformation est donnée en dessous de la figure.
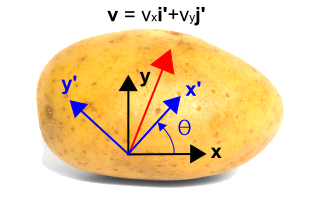
\\\N- On peut le voir en notant queCes quatre facteurs constituent les quatre termes des équations de transformation. On peut facilement les vérifier en définissant \(\theta = 0^\circ \) et \(\theta = 90^\circ \). Lorsque \(\theta = 0^\circ\), alors \(v’_x = v_x\) et \(v’_y = v_y\). Lorsque \(\theta = 90^\circ\), alors \(v’_x = v_y\) et \(v’_y = -v_x\).
Matrice de transformation
Il est plus pratique d’écrire (et de travailler avec) les équations de transformation en utilisant des matrices.
\\Gauche\{ \matrix {v_x \\\ v_y} \right\}]
Les termes \(\cos \theta\) sont sur la diagonale de la matrice tandis que les termes \(\sin \theta\) sont hors diagonale. Le seul problème potentiel est de se souvenir du terme \(\sin \theta\) qui porte le signe moins. C’est toujours le terme inférieur gauche.
L’équation ci-dessus s’écrit en notation matricielle sous la forme
où \({\bf Q}\) est la lettre habituelle choisie pour la matrice de transformation.

Matrices de transformation vs matrices de rotation
Si ce sujet n’était pas déjà assez difficile, de nombreux livres et sites web ajoutent à la confusion en ne clarifiant pas ce qui est fixe et ce qui est rotatif. Dans cette page et la suivante, c’est le système de coordonnées qui tourne alors que l’objet reste fixe.Ainsi, le terme matrice de transformation est utilisé ici pour le souligner.
Cependant, nous aborderons plus tard les situations dans lesquelles l’objet tourne alors que le système de coordonnées reste fixe. Dans ce scénario, le terme matrice de rotation sera utilisé pour souligner que l’objet tourne.
Une grande confusion provient du fait étonnant que chaque matrice (transformation et rotation) est juste la transposée de l’autre ! Elles ont donc un aspect extrêmement similaire. Dans les problèmes 2-D, la seule différence pratique est de savoir si le signe moins devant \(\sin \theta\) est sur le terme \(q_{12}\), ou le terme \(q_{21}\).
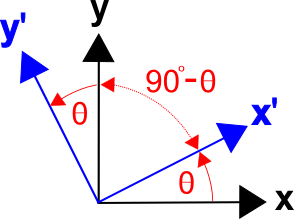
Une méthode générale existe pour formuler les matrices de transformation basées sur les cosinus des angles entre les axes des deux systèmes de coordonnées, c’est-à-dire les cosinus de direction. (Ceci s’applique également aux transformations 3-D.)La matrice de transformation peut être écrite comme
\\\N]
où \((x’,x)\) représente l’angle entre les axes \(x’\) et \(x\),\((x’,y)\) est l’angle entre les axes \(x’\) et \(y\), etc.
L’angle entre \(x’\) et \(y\) est \((90^\circ – \theta)\), et \(\cos(x’,y) = \cos(90^\circ – \theta) = \sin \theta\).
De même, l’angle entre \(y’\) et \(x\) est \((90^\circ + \theta)\), et \(\cos(y’,x) = \cos(90^\circ + \theta) = -\sin \theta\).
Notation tensorielle
La transformation des coordonnées s’écrit en notation tensorielle comme suit
\
où \(\lambda_{ij}\) est la matrice de transformation \({\bf Q}\). (Je ne sais pas pourquoi\({\bf Q}\) est utilisée dans la notation matricielle, mais \(\lambda_{ij}\), et non \(q_{ij}\), est utilisée dans la notation tensorielle). \(\lambda_{ij}\) est défini comme suit
\
Par exemple, si \(i = 1\) et \(j = 2\), alors
\
\(\lambda_{ij}\) est le cosinus directeur de l’angle entre l’axe \(x’_i\) et l’axe \(x_j\). Encore une fois, ceci est également applicable aux transformations 3-D.
Transformations en coordonnées 2D des tenseurs
Cette section présentera le quoi et le comment des transformations tensorielles.Le pourquoi devra attendre plus tard.
Les transformations en coordonnées des tenseurs de 2e rang impliquent la même matrice \({\bf Q}\)que les transformations vectorielles. Une transformation du tenseur de contrainte, \(\boldsymbol{\sigma}\), du système de coordonnées \(x-y\) de référence à \(\boldsymbol{\sigma’}\) dans un nouveau système \(x’-y’\) se fait comme suit.
En écrivant les matrices explicitement, on obtient
\ = \left \left \left \]
(Notez que le tenseur des contraintes est toujours symétrique, même après des transformations.)
En multipliant les matrices, on obtient
\
Ces trois équations sont exactement la transformée bidimensionnelle d’un tenseur de contraintes résultant de la sommation des forces sur un élément différentiel et de l’imposition de l’équilibre. Ceci est également représenté par le cercle de Mohr.
Notation tensorielle
La transformation des coordonnées est écrite en notation tensorielle comme
\
Comme d’habitude, la notation tensorielle fournit un aperçu supplémentaire du processus. Cette fois-ci, la compréhension vient des indices sur les lambdas. Chaque lambda associe effectivement un indice sur \(\boldsymbol{\sigma’}\) à un indice sur \(\boldsymbol{\sigma}\).Ceci est vrai quel que soit le rang du tenseur.
Transformations de vecteurs en coordonnées 3D
Plusieurs des équations générales utilisées dans les transformations 2-D sont également applicables en 3-D.Les exemples incluent
\
Seulement maintenant les détails sont différents. Les vecteurs ont des composantes z et les matrices de transformation sont 3×3 au lieu de 2×2.
\\N]
\N\N\N\N\N\N\N- \N- gauche{\N\N\N\N- matrice {v_x\N\N\N\N\N\N\N- v_z }
Transformations de coordonnées 3D de tenseurs
Une fois de plus, les règles ne changent pas, seuls les détails changent.
Ecrire les matrices explicitement donne
\ = \left\left\left\]
Cette page web effectue des transformations de coordonnées sur des tenseurs 3D. Essayez-la.
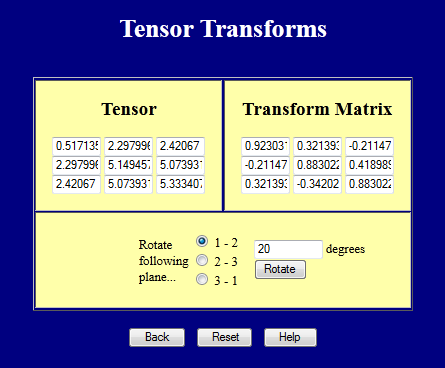
Transformations de coordonnées de tenseurs de 4e rang
Nous verrons dans la section sur la loi de Hooke que le tenseur de rigidité est de 4e rang, c’est-à-dire 3x3x3x3 (et non 4×4). Il s’écrit \(C_{ijkl}\) parce qu’il relie toute composante de déformation, \(\epsilon_{kl}\), à toute composante de contrainte, \(\sigma_{ij}\), c’est-à-dire, \La loi de transformation des coordonnées pour le tenseur de rigidité de rang 4 s’écrit facilement en notation tensorielle comme suit :
\
L’équation tensorielle indique comment écrire la transformation en notation matricielle.
\
Résumé
La transformation des coordonnées d’un vecteur en notation matricielle et tensorielle est
\
La transformation des coordonnées d’un tenseur en notation matricielle et tensorielle est
\Notez que \({\bf Q}\) et \(\lambda_{ij}\) sont la même matrice de transformation.
En 2-D, \({\bf Q}\) et \(\lambda_{ij}\) sont définis comme
\\\N]
qui est un cas particulier de la forme 3-D plus générale
\N\N\N\N