Hogyan készülj fel a matematika teszt geometriai kérdéseire
Általános információk
A geometria csak egy fantázianév a vonalak és formák tanulmányozására. Bizonyára vannak további bonyolult alapelvek és témakörök, de itt vannak az alapok. Ezeket kell elsajátítanod, mielőtt a haladóbb fogalmakkal foglalkoznál.
(Vedd figyelembe, hogy ha egy ábra ebben az útmutatóban “példa” felirattal szerepel, az nem feltétlenül az adott ábra egyetlen ábrázolása, hanem az egyik.)
Pontok és vonalak
A geometriában a pont egy hely. Nincs hossza, szélessége vagy mélysége. Egy pontot egy ponttal és egy nagybetűvel jelölünk.
A vonalszakaszt két pont és a köztük lévő összes pont határozza meg. A két pontot a szakasz végpontjainak nevezzük. A szegmensnek egy dimenziója van: a hossza. Egy szegmens írásához helyezzünk egy vonalat a két végpont fölé. \(\overline{AB}\) vagy \(\overline{BA}\) ez a szegmens:

A vonal mindkét irányban vég nélkül húzódik. Egy egyenes felírásához helyezzünk két nyíllal ellátott sávot a vonal két tetszőleges pontja fölé. \(\felül balra jobbra nyíl{AB}\) vagy \(\felül balra jobbra nyíl{BA}\) az egyenes:

Egy sugár egy végpontból indul és vég nélkül csak egy irányba terjed. Egy sugár felírásához helyezzünk egy jobbra mutató nyíllal ellátott sávot két pont fölé: a végpont és bármely más pont fölé (az adott irányban). \(\overrightarrow{AB}\) a sugár:

Figyelem: nem írhatunk olyan sugarat, amelynek a nyila balra mutat, mint \(\(\overleftarrow{BA}\). A sorrend is fontos. A \(\jobbra nyíllal{BA}\) nem ugyanaz, mint a \(\jobbra nyíllal{AB}\). Az első betű mindig a sugár kezdőpontja.
Két egyenes, szakasz vagy sugár merőleges, ha derékszöget zárnak be (lásd alább). A merőlegesség jelölésére a \(\perp\) szimbólumot használjuk. Például, ha \(\overline{AB}\) merőleges \(\overline{CD}\), akkor \(\overline{AB} \perp \overline{CD}\).
Példák: 
Két egyenes akkor párhuzamos, ha soha nem metszik egymást. Ha \(\jobbra-balra-felül{AB}\) párhuzamos \(\jobbra-balra-felül{CD}\), akkor azt írhatjuk, hogy \(\jobbra-balra-felül{AB} \paralel \jobbra-balra-felül{CD}\).
Példák: 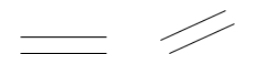
sík alakzatok
A geometriában a sík egy sík kétdimenziós felület, amely végtelen messzire nyúlik. A két dimenzió a hossz és a szélesség. A síkbeli alakzatok tehát olyan “sík” alakzatok, mint a négyzetek, körök és háromszögek.
Közönséges alakzatok
A sokszög egy zárt felület a síkon, amelyet oldalnak nevezett vonalszakaszok határolnak.
Példák: 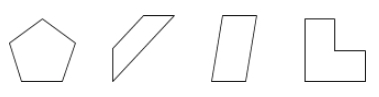
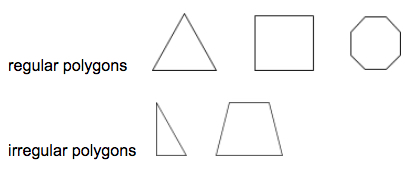
A szabályos sokszög olyan sokszög, amelyben minden szegmens és belső szög kongruens.
Példák:
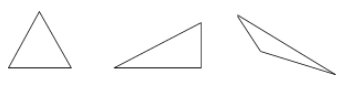
A háromszög egy háromoldalú sokszög.
Példák:
Négyszögek – négyoldalú sokszögek
A párhuzamos négyszög a négyszögek olyan típusa, amelynek ellentétes oldalai párhuzamosak és egybeesnek. A párhuzamosok szemközti szögei is egybeesnek.
Példák: 
A téglalap egy olyan paralelogramma, amelynek négy derékszöge van.
Példák: 
A rombusz olyan párhuzamos, amelynek mind a négy oldala egybeesik.
Példák:
A rombusz olyan párhuzamos, amelynek mind a négy oldala egybeesik: 
A négyzet egy olyan párhuzamos, amely egyszerre rombusz és téglalap (minden oldala egybeesik és minden szöge derékszögű).
Példák: A négyzet egy olyan párhuzamos, amely egyszerre rombusz és téglalap (minden oldala egybeesik és minden szöge derékszögű): 
A trapéz olyan négyszög, amelynek csak egy pár párhuzamos oldala van.
Példák: A trapéz egy olyan négyszög, amelynek csak egy párhuzamos oldala van: 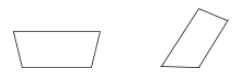
Négynél több oldalú sokszögek
\
\(^1\) A 11 oldalú sokszöget nevezhetjük endecogonnak vagy undecogonnak is.
Az alakzatok mérése
A kerület a sokszög körüli teljes távolság. A kerület kiszámításához egyszerűen csak össze kell adni az összes oldal hosszát. Ha a sokszög szabályos (minden oldala egybevágó), és az egyik oldal hossza \(s\), akkor az oldalak számát megszorozzuk \(s\)-vel, hogy megtaláljuk a kerületet. Például egy szabályos ötszög kerülete \(P_\text{reg ötszög}=5s\)