AC, of wisselstroom, wordt zo genoemd omdat de stroom wisselt of heen en weer wordt geschakeld tussen twee polariteiten. Met andere woorden, de stroom (en bijgevolg de spanning) is een functie van de tijd. Dit is fundamenteel verschillend van gelijkstroom, die een vaste polariteit heeft en over het algemeen constant is in de tijd. Een gelijkspanningsbron in een laboratorium, bijvoorbeeld, handhaaft idealiter een vaste spanning over zijn klemmen en varieert niet in de tijd. In tegenstelling daarmee kan een AC-golfvorm, als hij heen en weer zwaait door de tijd, grote variaties vertonen, variërend van de eenvoudige, regelmatige paden van laboratoriumstandaards zoals sinusgolven, driehoeksgolven en blokgolven, tot de veel complexere en golvende golfvormen die door muziekinstrumenten en de menselijke stem worden geproduceerd.
De sinusgolf is de eenvoudigste golf die kan worden gemaakt. Hij stelt de beweging voor van een eenvoudige vector die met een constante snelheid ronddraait, zoals de verticale verplaatsing van de secondewijzer van een klok. Een voorbeeld is te zien in figuur. Op de horizontale as staat de tijd. Deze neemt toe naarmate we van links naar rechts gaan (d.w.z. als punt A rechts van punt B ligt, dan komt A later in de tijd voor dan B). De verticale as wordt hier in het algemeen weergegeven als een percentage van het maximum, maar zou normaal een meting zijn van spanning, stroom, geluidsdruk of iets dergelijks.
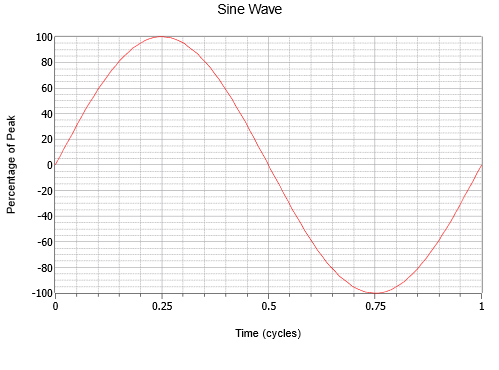
Figuurtje (Pagina-index{1}): Een sinusgolf.
Let op de vloeiende variatie die bij nul begint, een kwart stijgt naar een positieve piek, halverwege terugvalt naar nul, doorgaat naar een negatieve piek driekwart en dan weer stijgt naar het punt waar hij begon. Dit proces herhaalt zich vervolgens. Elke herhaling wordt een cyclus genoemd. In figuur is één volledige cyclus afgebeeld.
Sinusgolven vertonen kwartgolfsymmetrie. Dat wil zeggen dat elk kwart (in tijd) van de golf identiek is aan elk ander als je hem eenvoudig omdraait om de horizontale as en/of rechtop draait om zijn piek. De tijd die nodig is om één cyclus te voltooien wordt de periode genoemd en wordt aangeduid met het symbool (T) (voor tijd). De reciproke van de periode is de frequentie, \(f\).
De frequentie geeft aan hoeveel cycli er in één seconde zitten. Om een van de 19e eeuwse onderzoekers op dit gebied te eren, gebruiken we in plaats van de eenheid “cycli per seconde” Hertz, genoemd naar Heinrich Hertz en afgekort Hz. In figuur
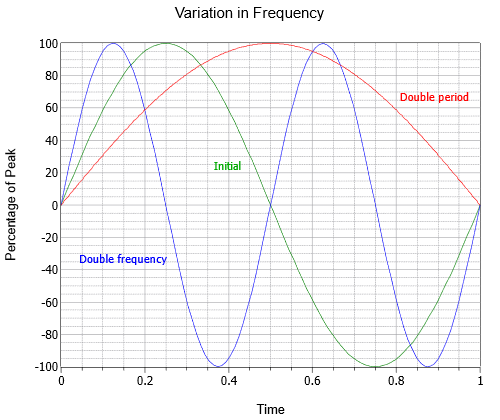
Figuur \(\PageIndex{2}\) zijn drie sinusgolven met verschillende frequenties te zien; de eerste golf (groen), een golf met tweemaal de frequentie (blauw), en een derde met de helft van de frequentie of tweemaal de periode (rood).
Figuur \(\PageIndex{2}\): Frequentievariatie van de sinusgolf.
De amplitude (verticaal) van de golf kan worden uitgedrukt als een piekgrootheid, die de verandering is vanaf de middelste nullijn tot aan de meest positieve waarde. De amplitude kan ook worden uitgedrukt als piek-tot-piek; de afstand van het meest negatieve tot het meest positieve. Voor een sinusgolf zal dit altijd tweemaal de piekwaarde zijn, hoewel dat niet het geval kan zijn voor andere golven die asymmetrisch kunnen zijn. Een reeks van drie sinusgolven met verschillende amplitudes is afgebeeld in figuur (blz. 3). Naast de oorspronkelijke (groen) zijn er versies met dubbele amplitude (blauw) en halve amplitude (rood).
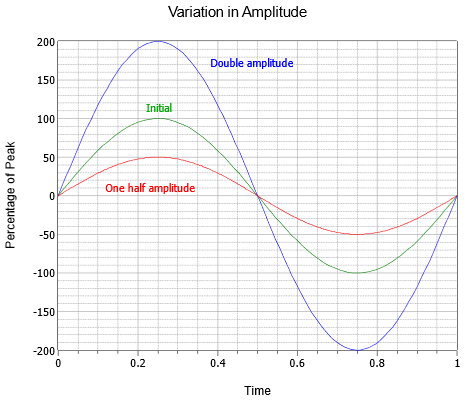
Figuur \(\PageIndex{3}\): Sinusgolf amplitude variatie.
Combinatie van deze parameters, beschouw de spanningsgolfvorm getoond in figuur \(PaginaIndex{4}\). Hier zien we twee cycli van een wisselspanningsgolfvorm.
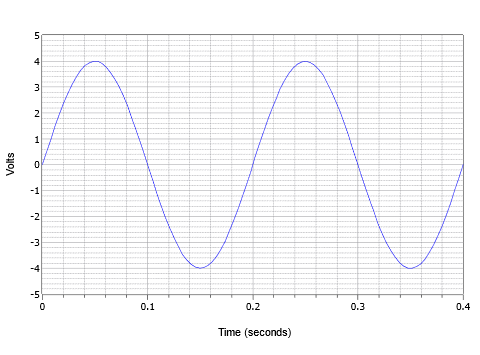
Figuur (\PageIndex{4}\): Basisvoorbeeld van een sinusgolf.
De piekwaarde is 4 volt en de piek-tot-piekwaarde is 8 volt (meestal afgekort als “8 V pp”). De periode van één cyclus is 0,2 seconden, oftewel 200 milliseconden (T = 200). Verder is de frequentie, \(f = 1/200\) milliseconden, of 5 Hz (5 cycli in één seconde).
AC-golfvormen kunnen ook worden gecombineerd met een DC-offset. Door een positief DC-niveau toe te voegen verschuift de golf verticaal omhoog, terwijl een negatief DC-niveau de golf verticaal omlaag verschuift. Dit verandert niets aan de frequentie of het AC-gedeelte van de amplitude (hoewel de absolute pieken door de DC-waarde zouden verschuiven). In figuur is het effect van verschillende DC-offsets te zien. Boven de eerste golf (groen) is een verder identieke golf met een positieve DC-offset gelijk aan 20% van de oorspronkelijke piekwaarde (blauw). Onder het origineel bevindt zich een derde golf (rood) met een negatieve DC-offset gelijk aan de helft van de piekwaarde van het origineel.
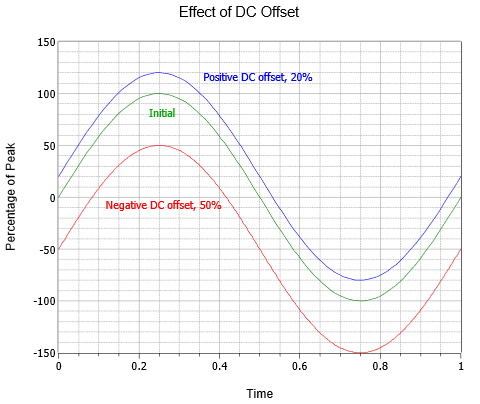
Figuur (Pagina-index{5}): Sinusgolf DC offset variatie.
Verder is het mogelijk dat een sinusgolf in de tijd verschuift ten opzichte van een andere sinusgolf of referentie. Hoewel het mogelijk is deze verschuiving als een absolute tijd aan te geven, is het gebruikelijker dit te doen als een faseverschuiving, dat wil zeggen, de tijd uitgedrukt als een deel van de periode in graden. Bijvoorbeeld, als een sinus een kwart van de periode voorloopt op een andere, dan wordt gezegd dat hij 90(1/4 van 360(^circ})) voorloopt. Bij een achterstand van ½ van de periode is er sprake van een achterstand van 180(^circ}) (d.w.z. een halve cyclus later in de tijd). Een andere manier om dit te zeggen is dat leidende golfvormen vroeger in de tijd beginnen en dus links van de referentie worden getekend, terwijl achterblijvende golfvormen later in de tijd beginnen en rechts worden getekend.
Figuur \(\PageIndex{6}\) illustreert het effect van faseverschuiving. Merk op dat in deze grafiek, \(t = 0) naar het midden van de horizontale as is verplaatst. De middelste kromme is de eerste, of referentiegolf (groen). Links (rood) is een golf die een achtste cyclus voorloopt op de eerste golf, ofwel 45%. Rechts (blauw) is een achterblijvende golf met de helft, ofwel -22,5.
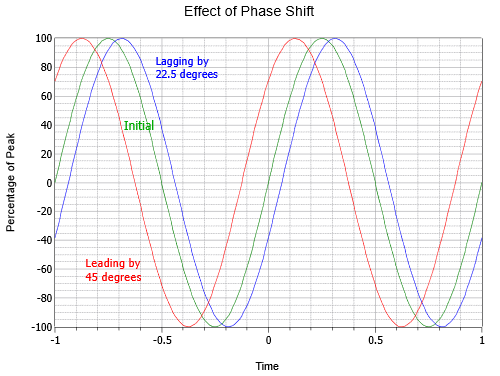
Figuur (Pagina-index{6}): Sinusgolf fasevariatie.
Door de voorgaande elementen te combineren, kunnen we een algemene indeling voor een sinusgolf ontwikkelen (spanning afgebeeld):
Waarbij
(v(t)\) de spanning op een bepaald tijdstip is,
(V_{DC}) de eventuele DC-offset is,
(V_{P}) de piekwaarde,
(f) is de frequentie,
(\theta) is de faseverschuiving (+ indien voorlopend en naar links getekend, – indien achterlopend en naar rechts getekend).
Voor een snel en praktisch voorbeeld, de golfvorm in figuur (\PageIndex{4}) heeft een amplitude van 4 volt piek, een frequentie van 5 Hz, en geen DC offset of faseverschuiving. De uitdrukking is dus v(t) = 4 sin (2 \pi 5 t)
Om een faseverschuiving te berekenen moet eerst het tijdverschil tussen de golfvorm en de referentie worden bepaald, dat we \(delta t) zullen noemen. De referentie kan een vast punt in de tijd zijn (b.v. t = 0) of een andere golfvorm. In het algemeen is de eenvoudigste manier om dit te doen het verschil te meten bij de nuldoorgangen, ervan uitgaande dat er geen DC-offset is. Is er wel een offset, dan moet de meting worden verricht op de plaats waar de nuldoorgang naar toe is verschoven (d.w.z. op het niveau van de DC-offset). Zodra het verschil is gevonden, deelt u het door de periode om de verschuiving als een fractie van een periode weer te geven. Aangezien één cyclus overeenkomt met één rotatie van de vector, of 360 graden, vermenigvuldigt u eenvoudig de breuk met 360 graden om de faseverschuiving in graden te vinden. Uitgedrukt in een formule:
Bedenk dat als de golf naar links is verschoven, hij voorloopt en positief is, terwijl een verschuiving naar rechts achterloopt of vertraagd is in de tijd, en dus negatief.
Voorbeeld \(\PageIndex{1}})
Schrijf de uitdrukking voor de golfvorm in figuur \(\PageIndex{7}}).
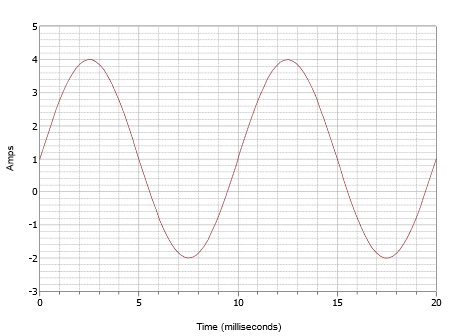
Figuur \(\PageIndex{7}}: Golfvorm voor voorbeeld \(\PageIndex{1}\).
Deze golfvorm lijkt oppervlakkig gezien op die in figuur \(\PageIndex{4}\), maar laat u daardoor niet misleiden. Allereerst is de tijdschaal anders. Voor deze golfvorm is één cyclus voltooid in 10 milliseconden. Daarom is de frequentie
Het tweede probleem is de DC-offset. Merk op dat de positieve piek bij 4 ampère optreedt, terwijl de negatieve piek bij -2 ampère optreedt. Dit wijst op een piek-topeak waarde van 6 ampère. Zonder offset zou de positieve piek bij 3 ampère liggen, daarom is er een DC-offset van +1 ampère. Het verticale midden van de golfvorm is omhoog verschoven van 0 ampère naar +1 ampère. Dit punt ligt op t = 0, daarom is er geen faseverschuiving. De resulterende uitdrukking is:
Voorbeeld \(\PageIndex{2})
Schrijf de uitdrukking voor de golfvorm in figuur \(\PageIndex{8})
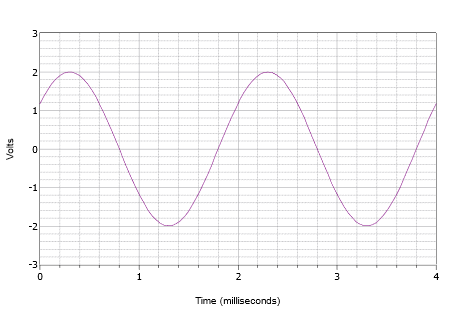
Figuur \(\PageIndex{8})
: Golfvorm voor voorbeeld \(\PageIndex{2}\).
Voreerst is de positieve piek 2 volt en de piek-tot-piek waarde is 4 volt. Er is dus geen DC offset. Het verticale midden van de golf begint niet op t = 0, dus moet er een faseverschuiving zijn. De waarde bij t = 0 is 1,2 volt. De golf bereikt dezelfde amplitude om \(t = 2\) milliseconden en begint een nieuwe cyclus te herhalen. De periode moet dus 2 milliseconden zijn. De frequentie is de reciproke van deze waarde, en dus f = 500 Hz.
De golfvorm is naar links verschoven, wat duidt op een positieve of voorlopende faseverschuiving. Als we de tweede cyclus bekijken, zien we dat deze bij 1,8 milliseconde nul volt bereikt. De verschuiving is dus 0,2 milliseconde. Uitgedrukt in graden is dit:
De uiteindelijke uitdrukking is:
Voorbeeld (\PageIndex{3})
Teken de golfvorm die bij de volgende uitdrukking hoort.
Merk eerst op dat de -3 volt offset de positieve piek omlaag duwt van 5 volt naar 2 volt, en de negatieve piek omlaag duwt van -5 volt naar -8 volt. De frequentie van 40 kHz geeft een periode van:
De faseverschuiving van -72(^{circ}) komt overeen met 72/360, ofwel 0,2 cycli. Dit komt overeen met een tijdvertraging (naar rechts verschoven omdat hij negatief is) van 0,2 maal 25 s, ofwel 5 s.
In eerste instantie is het vaak het beste om de plot via een aantal discrete stappen te construeren in plaats van te proberen het hele ding in één keer te tekenen. Teken eerst een sinusgolf met een piekamplitude van 5 volt en een periode van 25 s. Duw nu de golfvorm 3 volt omlaag, zodat de positieve piek nog maar 2 volt is en de negatieve piek -8 volt is. Tenslotte schuift u de verschoven golfvorm met 5 volt naar rechts. Het resultaat staat in figuur (\PageIndex{9}\).
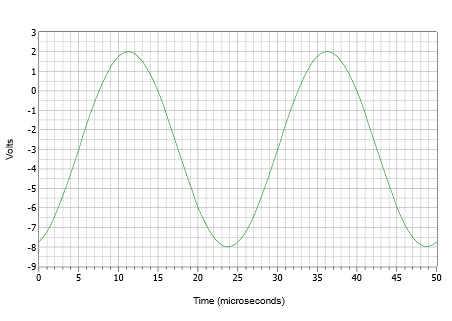
Figuur \(\PageIndex{9}\): Golfvorm voor voorbeeld
1.2.1: Laboratoriummetingen
In het laboratorium wordt een functiegenerator gebruikt om sinussen en andere golfvormen op te wekken. Met deze apparaten kunnen zowel de amplitude als de frequentie van de golf nauwkeurig worden geregeld en kan desgewenst een DC-offset worden toegevoegd. Een voorbeeld is te zien in figuur (Pagina-index{10}). Het bijbehorende meetinstrument is de oscilloscoop, of kortweg scoop.

Figuur (Pagina-index{10}\): Signaalgenerator voor het laboratorium.
De oscilloscoop is misschien wel het nuttigste en meest veelzijdige meetinstrument in het laboratorium. Gewoonlijk hebben zij twee of vier ingangskanalen, hoewel er meer mogelijk zijn. Elk ingangskanaal heeft zijn eigen gevoeligheidsinstelling en alle kanalen delen een gemeenschappelijke tijdreferentie. Het display tekent de golfvormen op dezelfde wijze als in de figuren [PageIndex{1}] – [PageIndex{9}]. Ook kunnen zij een spanning uitzetten tegen een andere (X – Y mode). Moderne oscilloscopen hebben extra functies zoals de automatische meting van frequentie, amplitude, faseverschuiving, enz., cursor-gebaseerde metingen, en de mogelijkheid om displaybeelden op te slaan als grafische bestanden. Een voorbeeld van een vierkanaals digitale oscilloscoop is te zien in Figuur (PaginaIndex{11}).

Figuur (PaginaIndex{11}): Een digitale oscilloscoop.
1.2.2: Schematische symbolen
Voor zover het schema’s betreft, zijn de symbolen voor wisselspannings- en stroombronnen afgebeeld in figuur (PaginaIndex{12}). De polariteits- en richtingsmarkeringen zijn niet absoluut; het gaat hier immers om wisselspanningsbronnen waarvan de polariteit en de richting heen en weer gaan. De markeringen worden in plaats daarvan gebruikt om een tijdsreferentie vast te stellen, vooral in schakelingen die gebruik maken van meerdere bronnen.
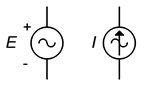
Figuur (PaginaIndex{12}\): Schematische symbolen voor een wisselspanningsbron (links) en een stroombron (rechts).
Het is de moeite waard om te onthouden dat het negeren van een bron hetzelfde is als het omdraaien van de polariteit. Dit was waar voor gelijkspanningsbronnen en blijft waar voor wisselstroombronnen. Dit wordt geïllustreerd in figuur (Pagina-Index{13}). Soms maakt het omdraaien of negeren van een bron de analyse iets duidelijker of gemakkelijker te visualiseren.
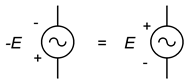
Figuur (Pagina-index{13}\): Polariteit/teken gelijkwaardigheid.
Voorbeeld \(\PageIndex{4})
Veronderstel dat een oscilloscoop twee golven weergeeft zoals afgebeeld in figuur \(\PageIndex{14}). Bepaal de faseverschuiving van de kleinere golfvorm met een piek van 20 volt (blauw) ten opzichte van de grotere golfvorm met een piek van 25 volt (rood).
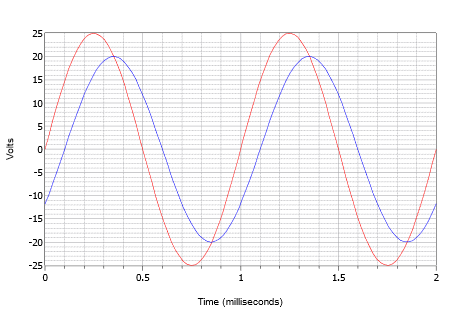
Figuur \(Pagina-index{14}\): Golfvormen voor voorbeeld (Pagina-index{4})
Vooreerst dient opgemerkt te worden dat geen van beide golven een DC-offset vertoont. Als een van beide golven een verschuiving zou vertonen, zouden de golven verticaal verschoven moeten worden, zodat hun normale nuldoorgangspunten op hetzelfde niveau zouden liggen. Bij meting van beide golven blijkt de periode 1 milliseconde te zijn. De tijdverschuiving kan het gemakkelijkst worden gevonden op een van de nuldoorgangen (er zijn vier plaatsen om uit te kiezen). De vertraging is één kleine afwijking, of 0,1 milliseconde, waarbij de kleinere golf in tijd is vertraagd, of achterloopt op de grotere golf. Dit duidt op een negatieve faseverschuiving.
1.2.3: Sinus en cosinus
Er zijn een handvol specifieke faseverschuivingen die de moeite waard zijn om nader te bekijken. Als een sinus omgekeerd is, dat wil zeggen ondersteboven gedraaid, is hij niet te onderscheiden van een sinus die +180 of -180 graden verschoven is. Met andere woorden, zo’n golf kan op drie verschillende manieren worden geschreven: \(- \sin (2 \pi ft)\), \(\sin (2 \pi ft – 180^{\circ})\), of \(\sin (2 \pi ft + 180^{\circ})\). Verder kan een sinusgolf die +90 graden is verschoven (dus naar links en naar voren) ook een cosinusgolf worden genoemd. Dus \sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). Tenslotte, als een sinus met -90 graden is verschoven (d.w.z. achterlopend en naar rechts), kan men spreken van een negatieve of omgekeerde cosinusgolf. Dus \sin (2 \pi ft – 90^{\circ}) = – \cos (2 \pi ft)\). Het verband tussen deze vier golven wordt geïllustreerd in figuur \(\PageIndex{15}\).
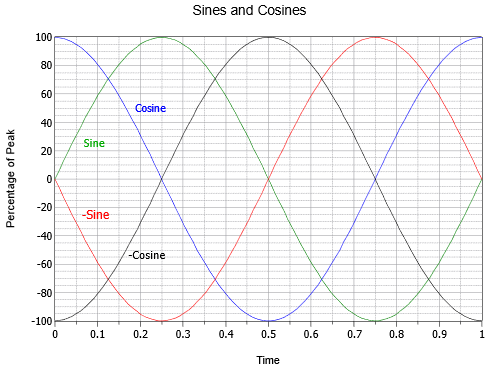
Figuur \(\PageIndex{15}\): Tijdsrelaties tussen sinussen en cosinussen.
Het is ook de moeite waard op te merken dat de cosinusgolf de eerste afgeleide, of helling, van de sinusgolf vertegenwoordigt. Zoals u zich wellicht herinnert van andere studies, is de helling of “steilheid” van een lijn de verhouding van de verticale verandering tot de horizontale verandering, soms “de stijging over de daling” genoemd. Voor een spanning is dit de verandering in spanning over de verandering in tijd, oftewel (Delta V/delta t). Voor een vloeiende, continu veranderende kromme als een sinusgolf is de helling op een bepaald punt juist gedefinieerd als de eerste afgeleide, of in dit geval \(dv/dt). Om visueel te controleren of dit waar is, zien we dat het steilste deel van de sinus (groen) het punt is waar de amplitude nul bereikt. Als de sinus de nul passeert terwijl hij positief beweegt (bij t = 0 of t = 1 in figuur), is de cosinus (blauw) op zijn positieve piek. Als de sinus door nul gaat terwijl hij negatief beweegt (bij t = 0,5), heeft de cosinus zijn negatieve piek. Verder is de sinus vlak met een helling van nul op zijn positieve en negatieve toppen (respectievelijk op \(t = 0,25) en \(t = 0,75)), en op die momenten is de amplitude van de cosinus ook nul. Het is ook waar dat de sinus de helling is van de negatieve cosinus, dat de negatieve cosinus de helling is van de negatieve sinus, en dat de negatieve sinus de helling is van de cosinus. In omgekeerde richting kunnen wij zeggen dat de anti-afgeleide (onbepaalde integraal) van een cosinusgolf een sinusgolf is, de integraal van een sinusgolf een negatieve cosinusgolf is, enzovoort. Deze relaties zullen het nuttigst blijken wanneer we onze aandacht richten op de respons van condensatoren en spoelen in wisselstroomkringen.
1.2.4: RMS – Root Mean Square Meting
Naast piek en piek-tot-piek kan de amplitude ook worden gegeven als een RMS-waarde (Root Mean Square). In feite, als piek of piek-tot-piek niet wordt gespecificeerd, wordt de meting verondersteld RMS te zijn. RMS is een speciale berekening die wordt gebruikt voor het vinden van equivalent gelijkstroomvermogen (zeer gebruikelijk, bijvoorbeeld bij audiovermogensversterkers). Met andere woorden, als we het vermogen in een weerstand willen vinden, moet de berekening worden uitgevoerd met RMS-waarden voor spanning of stroom, niet met piek- of toppuntwaarden. Doet men dit niet, dan zal dit resulteren in foutieve vermogens. Dit geldt ongeacht de golfvorm: sinusgolf, driehoeksgolf of de complexe golven van muzieksignalen. Indien een spanning als RMS wordt gespecificeerd, kan zij voor vermogensberekeningen worden behandeld als een gelijkwaardige gelijkspanning. Bijvoorbeeld, een 1 volt RMS sinus zal dezelfde vermogensdissipatie en verwarming in een gegeven weerstand veroorzaken als 1 volt gelijkspanning. Om deze reden wordt RMS soms de effectieve waarde genoemd (d.w.z. effectieve DC-waarde).
De naam wortel-gemiddelde-kwadraat beschrijft het proces van het bepalen van de effectieve waarde. Allereerst moet men bedenken dat het vermogen evenredig is met het kwadraat van de spanning of stroom. Onze eerste stap is dus het kwadrateren van de ingangsgolfvorm. Natuurlijk is de golfvorm een functie van de tijd en het kwadraat ervan zal een nieuwe vorm opleveren. Op dit punt moeten wij de gemiddelde waarde van deze nieuwe vorm vinden. De reden hiervoor is eenvoudig, maar niet noodzakelijk voor de hand liggend. Elektrische en elektronische componenten hebben massa, en warmen of koelen dus niet onmiddellijk af. Zij vertonen een thermische tijdconstante. Daarom reageren zij op de gemiddelde input in de tijd. Hoewel we een “momentaan piekvermogen” kunnen berekenen op een bepaald moment in de tijd, geeft dit niet het gelijkwaardige DC-vermogen weer. Zodra wij de gemiddelde waarde van deze gekwadrateerde golfvorm hebben verkregen, is de overeenkomstige gelijkstroomwaarde slechts de vierkantswortel van het gemiddelde. Het resultaat is een fractionele waarde tussen nul en één die wordt gebruikt als een schaalfactor om een piekwaarde in een RMS-waarde om te zetten. De waarde is uniek voor de specifieke golfvorm. Dat wil zeggen, alle sinussen (ongeacht fase) hebben dezelfde factor, alle regelmatige driehoeksgolven hebben dezelfde factor, enzovoort. Omdat we ons vooral met sinussen bezighouden, gaan we nader in op het bepalen van de RMS-factor voor sinussen.
We beginnen met de basisuitdrukking voor een sinusgolf zonder DC-offset of faseverschuiving, en met een amplitude van één:
De eerste stap is het kwadrateren van deze golfvorm. Een bruikbare goniometrische identiteit is
Toepassing hiervan op onze golf levert op:
Deze uitdrukking beschrijft een omgekeerde cosinusgolf met tweemaal de oorspronkelijke frequentie en de helft van de oorspronkelijke amplitude, met een gelijkstroomverschuiving gelijk aan de piekwaarde. Met andere woorden, de negatieve top van de cosinus ligt op nul en de positieve top op 1. De volgende stap is het gemiddelde of de gemiddelde waarde van dit tussenresultaat te vinden. Het gemiddelde is gelijk aan de verschuiving van 0,5. Dit kan worden gevisualiseerd als het gebied boven de offset dat de “dip” onder de offset perfect opvult. De laatste stap is het nemen van de vierkantswortel uit het gemiddelde. De vierkantswortel van 0,5 is gelijk aan één over de vierkantswortel van twee, of ongeveer 0,707. De RMS-waarde is dus 0,707 maal de piek. Als alternatief kan men de piek delen door de vierkantswortel van twee, of ongeveer 1,414. Dit proces wordt grafisch weergegeven in Figuur \(\PageIndex{16}\).
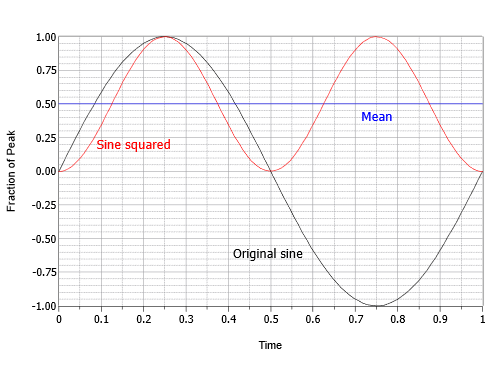
Figuur \(\PageIndex{16}\): Proces om RMS-factor voor sinussen te vinden.
Samengevat is RMS voor sinusgolven altijd de piekwaarde maal 0,707. We kunnen ook zeggen dat de RMS-waarde van een sinus gelijk is aan de piekwaarde gedeeld door ongeveer 1,414. Nogmaals, deze verhoudingen zouden niet noodzakelijkerwijs waar zijn voor niet-sinusgolven. Bijzonderheden betreffende andere veel voorkomende vormen zijn te vinden in aanhangsel C. Tenslotte wordt de verhouding van de piekwaarde tot de RMS-waarde de topverhouding genoemd. Dit is een vaste waarde voor sinusgolven (ook hier ongeveer 1,414), maar kan meer dan 10:1 zijn voor sommige soorten audiosignalen.
1.2.5: Golflengte
Een ander punt van belang is de voortplantingssnelheid van de golf. Deze varieert sterk. In het geval van licht in een vacuüm (of bij benadering een elektrische stroom in een draad) is de snelheid ongeveer 3E8 meter per seconde (d.w.z. 300.000 km/s) of ongeveer 186.000 mijl per seconde.
Gegeven aan een snelheid en een periode, kunnen wij ons voorstellen hoe ver de pieken van de golf uit elkaar liggen. Deze afstand wordt de golflengte genoemd en wordt aangeduid met de Griekse letter lambda (lambda). De golflengte is gelijk aan de snelheid gedeeld door de frequentie, \(\lambda = v/f\). Voor een luidspreker die een sinus van 100 Hz voortbrengt, is de geluidssnelheid in lucht 344 m/s, dus \lambda = 344 m/s / 100 Hz, of 3,44 meter (iets meer dan 11 voet). Merk op dat hoe hoger de frequentie, hoe korter de golflengte. Merk ook op dat hoe sneller de snelheid, hoe langer de golflengte. Golflengteberekeningen zijn van bijzonder belang op het gebied van telecommunicatie en akoestiek.