Inleiding
Coordinatentransformaties zijn al onintuïtief genoeg in 2-D, en in 3-D bijzonder pijnlijk. Deze pagina behandelt ze in de volgende volgorde: (i) vectoren in 2D, (ii) tensoren in 2D, (iii) vectoren in 3D, (iv) tensoren in 3D, en tenslotte (v) tensortransformaties van de vierde rang.
Een belangrijk aspect van coördinatentransformaties is de evaluatie van de transformatiematrix, vooral in 3-D. Dat wordt hier aangestipt, en op de volgende bladzijde uitvoerig besproken.
Het is zeer belangrijk te beseffen dat alle coordinatentransformaties op deze bladzijde rotaties van het coordinatensysteem zijn terwijl het “object” zelf vast blijft. Het “voorwerp” kan een vector zijn, zoals kracht of snelheid, of een tensor, zoals spanning of rek in een component. Objectrotaties worden in latere secties besproken.
2-D coördinatentransformaties van vectoren
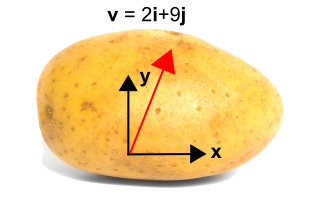
De academische aardappel geeft een uitstekend voorbeeld van hoe coördinatentransformaties van toepassing zijn op vectoren, terwijl tegelijkertijd wordt benadrukt dat het coördinatenstelsel roteert en niet de vector… of aardappel.
De aardappel links heeft een vector op zich. Maar zonder een assenstelsel is er geen manier om de vector te beschrijven. Dus is er een assenstelsel aan de aardappel toegevoegd, zoals rechts te zien is, waardoor de vector nu beschreven kan worden als.

Dus nu introduceren we een geroteerd coördinatenstelsel, hieronder in blauw weergegeven, met behulp van x’en y’en. Het nieuwe systeem is tegen de wijzers van de klok in geroteerd met een hoek, \theta), ten opzichte van het oorspronkelijke coördinatenstelsel. Merk op dat de vector zelf helemaal niet verandert. Het is nog steeds dezelfde vector als voorheen. Maar hij wordt beschreven door andere numerieke waarden in het nieuwe assenstelsel. In dit geval is de vector meer evenwijdig met de nieuwe x-as dan met de y-as, zodat de i-component groter zal zijn dan de j-component. De transformatie is onder de figuur gegeven.
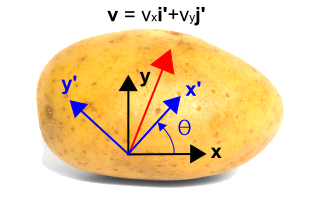
Dit is te zien door op te merken datDeze vier factoren vormen de vier termen in de transformatievergelijkingen. Ze zijn eenvoudig te controleren door \theta = 0 ^circ \) en \theta = 90 ^circ \). Als \theta = 0^circ \), dan is \(v’_x = v_x\) en \(v’_y = v_y\). Als \theta = 90 ^circ), dan is \(v’_x = v_y) en \(v’_y = -v_x).
Transformatiematrix
Het is handiger om transformatievergelijkingen te schrijven (en ermee te werken) met behulp van matrices.
Links{ \matrix {v_x \ v_y} \De termen van de matrix staan op de diagonaal en de termen van de matrix staan off-diagonaal. De enige mogelijke moeilijkheid is onthouden welke term het minteken heeft. Het is altijd de term linksonder.
De bovenstaande vergelijking wordt in matrixnotatie geschreven als
waarbij ({Q}) de gebruikelijke letter is die voor de transformatiematrix is gekozen.

Transformatie- vs. Rotatiematrices
Als dit onderwerp al niet moeilijk genoeg was, maken veel boeken en websites de verwarring nog groter door niet duidelijk te maken wat vast is en wat roteert. In deze en de volgende pagina’s is het het coordinatensysteem dat roteert terwijl het object vast blijft. Dus de term transformatiematrix wordt hier gebruikt om dit te benadrukken.
Hoewel we later situaties zullen behandelen waarin het object roteert terwijl het coordinatensysteem vast blijft. In dit scenario zal de term rotatiematrix worden gebruikt om te benadrukken dat het voorwerp roteert.
Veel verwarring ontstaat door het verbazingwekkende feit dat elke matrix (transformatie en rotatie) slechts de transpositie is van de andere! Ze lijken dus sterk op elkaar. Bij 2D problemen is het enige praktische verschil of het minteken voor de term q_{12} of de term q{21} staat.
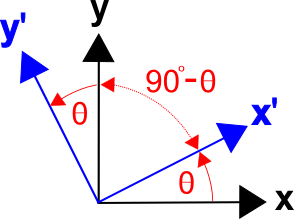
Er bestaat een algemene methode om transformatiematrices te formuleren op basis van de cosinussen van de hoeken tussen de assen van de twee coördinatenstelsels, de richtingcosinussen. (Dit geldt ook voor 3-D transformaties.)De transformatiematrix kan geschreven worden als
waarin ((x’,x)\) de hoek is tussen de assen x en x, \((x’,y)\) de hoek is tussen de assen x en y, enz.
De hoek tussen x’en en y’is (90 ^circ – \theta)\), en \(\cos(x’,y) = \cos(90 ^circ – \theta) = \sin \theta).
Ook de hoek tussen \(y’¢) en \(x’¢) is \(90^circ + \theta)\), en \(\cos(y’,x) = \cos(90^circ + \theta) = -\sin \theta).
Tensor-notatie
De coördinatentransformatie wordt in tensor-notatie geschreven als
waarbij \(\lambda_{ij}}) de transformatiematrix \({\bf Q}}) is. (Ik weet niet waarom \lambda_{ij}\) in matrixnotatie wordt gebruikt, maar \lambda_{ij}\), en niet \q_{ij}\), wordt gebruikt in tensornotatie). \(\lambda_{ij}\) is gedefinieerd als
Bijvoorbeeld, als \(i = 1) en \(j = 2), dan is
(\lambda_{ij}\) de richtingscosinus van de hoek tussen de as van \(x’_i\) en de as van \(x_j\). Ook dit geldt weer voor 3D-transformaties.
2-D coördinatentransformaties van tensoren
In deze paragraaf zullen we het wat en hoe van tensortransformaties behandelen. Het waarom zal tot later moeten wachten.
Coordinatentransformaties van 2e rang tensoren hebben betrekking op precies dezelfde matrix als vectortransformaties. Een transformatie van de spanningstensor, \(\boldsymbol{\sigma}},van het referentie x-y coördinatensysteem naar \(\boldsymbol{sigma’}}) in een nieuw x’-y’-systeem gebeurt als volgt.
Het expliciet uitschrijven van de matrices geeft
= \links \links \left \(Merk op dat de spanningstensor altijd symmetrisch is, zelfs na transformaties.)
Multiplicatie van de matrices geeft
Deze drie vergelijkingen zijn precies de 2D-transformatie van een spanningstensor die volgt uit het optellen van krachten op een differentieelelement en het opleggen van een evenwicht. Dit wordt ook voorgesteld door de cirkel van Mohr.
Tensor-notatie
De coördinatentransformatie wordt in tensor-notatie geschreven als
Zoals gebruikelijk geeft de tensor-notatie extra inzicht in het proces. Deze keer komt het inzicht van de subscripts op de lambda’s. Elke lambda koppelt effectief een subscript op \(\boldsymbol{\sigma}}) aan een op \(\boldsymbol{\sigma}}). Dit is waar ongeacht de rang van de tensor.
3-D coördinatentransformaties van vectoren
Veel van de algemene vergelijkingen die gebruikt worden in 2-D transformaties zijn ook toepasbaar in 3-D. Voorbeelden zijn
Alleen zijn nu de details anders. De vectoren hebben z-componenten en de transformatiematrices zijn 3×3 in plaats van 2×2.
3-D coördinatentransformaties van tensoren
Ook hier veranderen de regels niet, alleen de bijzonderheden.
De matrices expliciet uitschrijven geeft
= \left\left\left\left]
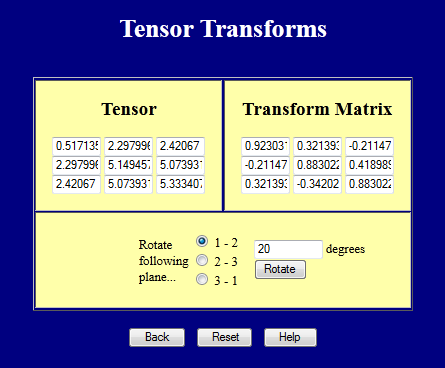
Deze webpagina voert coördinatentransformaties uit op 3-D tensoren. Probeer het maar eens uit.
Coordinaattransformaties van 4-rangs tensoren
We zullen in het hoofdstuk over de wet van Hooke zien dat de stijfheidstensor van de 4e rang is, d.w.z. 3x3x3x3 (niet 4×4). Hij wordt geschreven als C(C_{ijkl}) omdat hij elke deformatiecomponent, \(\epsilon_{kl}), relateert aan elke spanningscomponent, \(\sigma_{ij}), d.w.z., \De coördinatentransformatiewet voor de 4e rangs stijfheidstensor kan eenvoudig in tensornotatie geschreven worden als
De tensorvergelijking geeft aan hoe de transformatie in matrixnotatie geschreven moet worden.
Samenvatting
De coördinatentransformatie van een vector in matrix- en tensornotatie is
De coördinatentransformatie van een tensor in matrix- en tensornotatie is
Opgemerkt moet worden dat \({\bf Q}\) en \(\lambda_{ij}\) dezelfde transformatiematrix zijn.
.