Proportioneel is slechts één manier om op een fout in het systeem te reageren. Het probleem met proportionele regeling is dat deze geen trends kan detecteren en zich daaraan kan aanpassen. Dit is de taak van integrale regeling.
Er is nog een voorbeeldgrafiek van de fout in een systeem in de tijd links in figuur 6. Ook hier kan het gaan om de afstand van een robot tot een object, of om het vloeistofniveau in een tank, of de temperatuur in een fabrieksoven. Misschien blijft het doel dat de robot volgt van de robot weggaan met een snelheid die de robot niet kan inhalen. Misschien is de afdichting van de ovendeur versleten, of wordt er ongebruikelijk veel vloeistof uit de tank gehaald. Wat de oorzaak ook is, aangezien proportionele besturing niet is ontworpen om te reageren op trends, kan zij het probleem niet detecteren en corrigeren. Dat is waar integrale regeling in beeld komt.
Integraal meet het gebied tussen de foutwaarden en de tijdas. Als de fout niet naar nul terugkeert, wordt het gebied van de fout groter en groter. De rechterkant van figuur 6 laat zien hoe de uitvoer van de integraal op een dergelijke trend kan reageren. Naarmate het gebied tussen de foutkromme en de tijdas toeneemt, neemt de uitvoer evenredig met dit gebied toe. Het resultaat is dat de uitvoer de actuator steeds harder drijft om de fout te corrigeren.
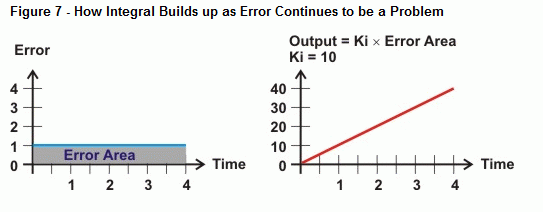
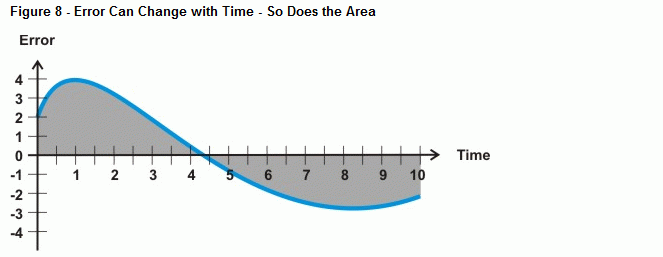
Wat gebeurt er nu als de fout geen rechte lijn is, zoals de curve in figuur 8? Dat is wat de rekenkundige bewerking van de integratie bepaalt, het gebied tussen een kromme en een as. In het geval van integrale besturing groeit, naarmate er meer tijd verstrijkt met een fout, het gebied onder de curve, en daarmee de waarde die de integrale berekening zal gebruiken om tegen de systeemfout in te sturen. Als de foutcurve onder de tijdas daalt, wordt de opbouw van negatief gebied afgetrokken van de opbouw van positief gebied. Bij een juiste afstelling kan de integrale besturing het systeem helpen zich te richten op een fout van nul.
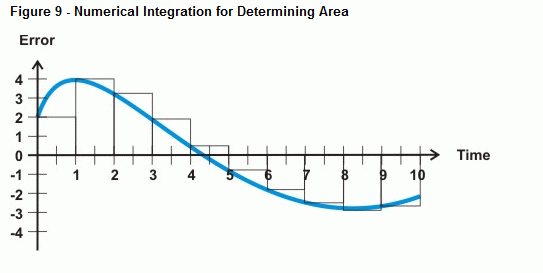
De BASIC-amp kan de fout onder de curve benaderen met numerieke integratie. In figuur 9 ziet u hoe u de fout onder een kromme kunt benaderen door de oppervlakte van een aantal kleine rechthoekjes tussen de foutcurve en de tijdas bij elkaar op te tellen. Het oppervlak van elk vakje is de fout vermenigvuldigd met de tijd tussen de metingen. Door alle vakjes bij elkaar op te tellen, krijgt u een benadering van het gebied onder de curve.
Zolang uw metingen gelijkmatig verdeeld zijn, kunt u de breedte van elk vakje de waarde 1 geven. Dit maakt de berekening veel eenvoudiger dan te proberen rekening te houden met 20 ms tussen monsters, 5 minuten tussen monsters, of wat uw bemonsteringsfrequentie ook blijkt te zijn. In plaats van de fout te vermenigvuldigen met de tijd tussen de metingen en dan op te tellen bij de volgende fout vermenigvuldigd met tijd, kunt u gewoon elke foutmeting vermenigvuldigen met een tijd van 1. Het resultaat is dat u gewoon een lopend totaal van foutmetingen kunt bijhouden voor uw integrale berekening. Hier is een voorbeeld van hoe dit te doen met PBASIC:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
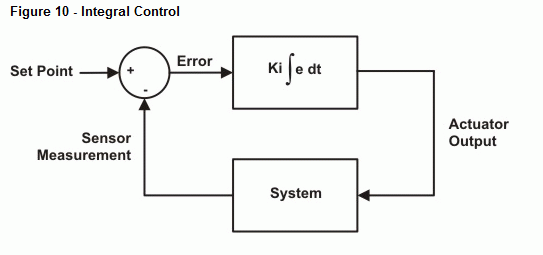
Het volgende voorbeeldprogramma voert numerieke integratie uit op het foutsignaal en past de uitgang dienovereenkomstig aan. Net als bij proportionele regeling is er een constante die de integratie-uitgang schaalt naar de gewenste waarde. Om het eenvoudig te houden, gebruiken we voor Ki weer 10. Figuur 10 toont een blokschema van de regelkring. De term Kp ∫ edt verwijst naar Kp vermenigvuldigd met de integraal van de fout in de tijd. Met andere woorden, Kp vermenigvuldigd met het geaccumuleerde gebied tussen de foutcurve en de tijdas.
Voorbeeldprogramma – IntegralAlgorithm.bs2
- Invoeren, opslaan en uitvoeren van IntegralAlgorithm.bs2.
- Voer deze reeks waarden in het venster Zenden van de Debug Terminal in: 3 3 3 3 3 3 3 3 3. Merk op hoe de integrale uitvoer groter wordt elke keer als de 3 wordt herhaald. Dat is de taak van de integraal, om trends te detecteren en de aandrijving te vergroten om te corrigeren als dat nodig is.
- Nou probeer deze reeks: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. Het gebied onder deze kromme is 0 omdat het negatieve gebied hetzelfde is als het positieve gebied. Dat is ook waar de integraalberekening op uitkomt als u klaar bent met het invoeren van de reeks.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Hoe IntegralAlgorithm.bs2 werkt
Dit programma is een ProportionalAlgorithm.bs2 dat is aangepast om in plaats daarvan de integraalberekening uit te voeren. Er zijn nu twee verschillende soorten fouten om bij te houden, dus werd de foutvariabele array uitgebreid tot twee elementen. De variabele error(0) volgt de huidige fout, en error(1) volgt de geaccumuleerde fout. De constanten Current CON 0 en Accumulator CON 1 maken de boekhouding een beetje zinvoller met error(current) en error(accumulator).
De andere verandering die werd aangebracht is dat de fout wordt geaccumuleerd en de integrale uitgang wordt berekend met deze twee statements:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Jouw beurt – Het klemmen van de integrale uitgang
Zoals u wellicht hebt begrepen van het herhaaldelijk invoeren van 3 in de Debug Terminal, kan de integrale uitgang van de aandrijving echt beginnen weg te lopen. U kunt de MIN en MAX operatoren gebruiken om te voorkomen dat de integrale besturing te ver gaat met de uitvoer. Laten we de servo offset activiteit herhalen en de output beperken van 650 tot 850.
- Verander het drive = i statement in drive = i + Offset MIN 650 MAX 850.
- Run het programma en controleer dat de integrale output wordt beperkt tot waarden tussen 650 en 850. Probeer herhaaldelijk 2 in te voeren, dan -2 herhaaldelijk.