Hoe bereid je je voor op de Geometrie Vragen op een Wiskunde Test
Algemene informatie
Geometrie is gewoon een mooie naam voor de studie van lijnen en vormen. Er zijn zeker nog meer moeilijke principes en onderwerpen, maar we hebben hier de basis. Je moet deze onder de knie hebben voordat je meer geavanceerde concepten aansnijdt.
(Houd er rekening mee dat als een figuur in deze gids als “voorbeeld” wordt aangeduid, dit misschien niet de enige voorstelling van die figuur is, maar wel één ervan.)
Punten en lijnen
Een punt in de meetkunde is een plaats. Het heeft geen lengte, breedte of diepte. We gebruiken een punt en een hoofdletter om een punt aan te geven.
Een lijnstuk wordt gedefinieerd door twee punten en alle punten daartussen. De twee punten worden eindpunten van het lijnstuk genoemd. Een lijnstuk heeft één dimensie: lengte. Om een lijnstuk te schrijven, zet je een balkje over de twee eindpunten. \Een lijnstuk strekt zich in beide richtingen uit zonder einde. Om een lijn te schrijven, plaats je een balk met twee pijlen over twee willekeurige punten van de lijn. \Een rechte begint bij één eindpunt en strekt zich zonder eind in slechts één richting uit. Om een halfrechte te schrijven, plaatst men een balkje met een pijl naar rechts over twee punten: het eindpunt en een ander punt (in die richting). \Een halfrechte is een halfrechte:

Note: je kunt geen halfrechte schrijven met de pijl naar links, zoals bij \(\overleftarrow{BA}\). Ook de volgorde is belangrijk. \(\overleftarrow{BA}\) is niet hetzelfde als \(\overleftarrow{AB}\). De eerste letter is altijd het beginpunt van een halfrechte.
Twee rechten, lijnstukken of stralen staan loodrecht op elkaar als ze een rechte hoek vormen (zie hieronder). Gebruik het symbool ‖ om de loodlijn aan te geven. Bijvoorbeeld, als (\overline{AB}) loodrecht staat op \overline{CD}}, dan kun je schrijven (\overline{AB}) \perp \overline{CD}}).
Voorbeelden: 
Twee lijnen zijn evenwijdig als ze elkaar nooit snijden. Als (\overleftrightarrow{AB}) evenwijdig is aan \overleftrightarrow{CD}}, dan kun je schrijven \overleftrightarrow{AB} \parallel \overleftrightarrow{CD}}).
Voorbeelden: 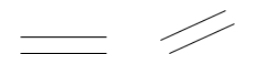
Vlakke Vormen
In de meetkunde is een vlak een plat tweedimensionaal vlak dat zich oneindig ver uitstrekt. De twee dimensies zijn lengte en breedte. Platte vormen zijn dus “platte” vormen, zoals vierkanten, cirkels en driehoeken.
Gemeenschappelijke vormen
Een veelhoek is een gesloten oppervlak op een vlak begrensd door lijnstukken die zijden worden genoemd.
Voorbeelden: 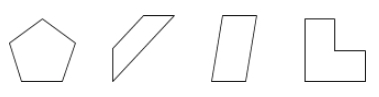
Een regelmatige veelhoek is een veelhoek waarin alle lijnstukken en binnenhoeken congruent zijn.
Voorbeelden:
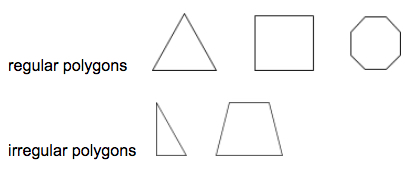
Een driehoek is een driezijdige veelhoek.
Voorbeelden:
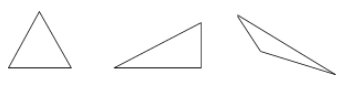
Quadrilateralen – vierzijdige veelhoeken
Een parallellogram is een type vierhoek waarvan de overstaande zijden evenwijdig en congruent zijn. Tegenoverliggende hoeken van een parallellogram zijn ook congruent.
Voorbeelden: 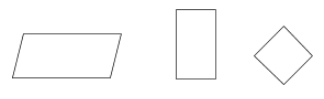
Een rechthoek is een parallellogram met vier rechte hoeken.
Voorbeelden: 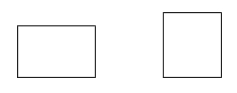
Een ruit is een parallellogram waarvan alle vier zijden congruent zijn.
Voorbeelden: 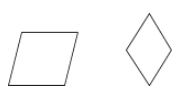
Een vierkant is een parallellogram dat zowel een ruit als een rechthoek is (alle zijden zijn congruent en alle hoeken zijn recht).
Voorbeelden: 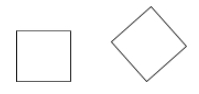
Een trapezium is een vierhoek met slechts één paar evenwijdige zijden.
Voorbeelden: 
Polygonen met meer dan vier zijden
Een veelhoek met 11 zijden kan ook een endecagon of een undecagon genoemd worden.
Het meten van vormen
De omtrek is de totale afstand rond een veelhoek. Om de omtrek te vinden, tel je de lengtes van alle zijden bij elkaar op. Als de veelhoek regelmatig is (alle zijden zijn congruent) en de lengte van één zijde is, vermenigvuldig dan het aantal zijden met de lengte van één zijde om de omtrek te vinden. Bijvoorbeeld, de omtrek van een regelmatige vijfhoek is \(P_text{reg vijfhoek}=5s)