Minder…![]()
Er zijn vele formules van ![]() van vele soorten. Deze omvatten onder andere reeksen, producten, meetkundige constructies, limieten, speciale waarden, en pi iteraties.
van vele soorten. Deze omvatten onder andere reeksen, producten, meetkundige constructies, limieten, speciale waarden, en pi iteraties.
![]() is nauw verbonden met de eigenschappen van cirkels en bollen. Voor een cirkel met straal
is nauw verbonden met de eigenschappen van cirkels en bollen. Voor een cirkel met straal ![]() , zijn de omtrek en oppervlakte gegeven door
, zijn de omtrek en oppervlakte gegeven door
|
(1)
|
|||
|
(2)
|
Zo ook voor een bol met straal ![]() , zijn de oppervlakte en het volume van de bol
, zijn de oppervlakte en het volume van de bol
|
(3)
|
|||
|
(4)
|
Een exacte formule voor ![]() in termen van de inverse raaklijnen van eenheidsfracties is de formule van Machin
in termen van de inverse raaklijnen van eenheidsfracties is de formule van Machin
|
(5)
|
Er zijn nog drie andere Machin-achtige formules, evenals duizenden andere soortgelijke formules met meer termen.
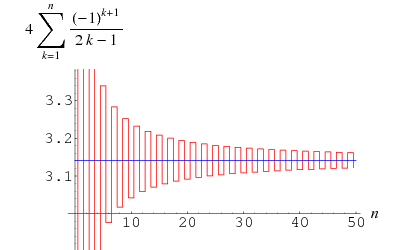
Gregory en Leibniz vonden
|
(6)
|
|||
|
(7)
|
(Wells 1986, p. 50), die bekend staat als de Gregory-reeks en kan worden verkregen door ![]() in de Leibniz-reeks voor
in de Leibniz-reeks voor ![]() te pluggen. De fout na de
te pluggen. De fout na de ![]() e term van deze reeks in de Gregorius-reeks is groter dan
e term van deze reeks in de Gregorius-reeks is groter dan ![]() zodat deze som zo langzaam convergeert dat 300 termen niet voldoende zijn om
zodat deze som zo langzaam convergeert dat 300 termen niet voldoende zijn om ![]() tot op twee decimalen nauwkeurig te berekenen! Het kan echter worden getransformeerd tot
tot op twee decimalen nauwkeurig te berekenen! Het kan echter worden getransformeerd tot
|
(8)
|
waar ![]() de Riemann zeta-functie is (Vardi 1991, pp. 157-158; Flajolet en Vardi 1996), zodat de fout na
de Riemann zeta-functie is (Vardi 1991, pp. 157-158; Flajolet en Vardi 1996), zodat de fout na ![]() termen
termen ![]() bedraagt.
bedraagt.
Een oneindige somreeks naar Abraham Sharp (ca. 1717) wordt gegeven door
|
(9)
|
(Smith 1953, p. 311). Bijkomende eenvoudige reeksen waarin ![]() voorkomt zijn
voorkomt zijn
|
(10)
|
|||
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
|||
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
(Wells 1986, p. 53).
In 1666, gebruikte Newton een meetkundige constructie om de formule
|
(18)
|
|||
|
(19)
|
waarmee hij ![]() berekende (Wells 1986, p. 50; Borwein et al. 1989; Borwein and Bailey 2003, pp. 105-106). De coëfficiënten kunnen worden gevonden uit de integraal
berekende (Wells 1986, p. 50; Borwein et al. 1989; Borwein and Bailey 2003, pp. 105-106). De coëfficiënten kunnen worden gevonden uit de integraal
|
(20)
|
|||
|
(21)
|
door de reeksuitbreiding te nemen van ![]() over 0, obtaining
over 0, obtaining
|
(22)
|
(OEIS A054387 en A054388). Gebruik van de convergentieverbeteringstransformatie van Euler geeft
|
(23)
|
|||
|
(24)
|
|||
|
(25)
|
(Beeler et al. 1972, punt 120).
Dit komt overeen met het inpluggen van ![]() in de machtsreeks voor de hypergeometrische functie
in de machtsreeks voor de hypergeometrische functie ![]() ,
,
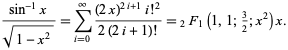 |
(26)
|
Ondanks de convergentieverbetering convergeert reeks (◇) slechts op één bit/term. Ten koste van een vierkantswortel heeft Gosper opgemerkt dat ![]() 2 bits/term oplevert,
2 bits/term oplevert,
|
(27)
|
en ![]() geeft bijna 3.39 bits/term,
geeft bijna 3.39 bits/term,
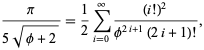 |
(28)
|
waar ![]() de gulden snede is. Gosper verkreeg ook
de gulden snede is. Gosper verkreeg ook
|
(29)
|
Een spigot-algoritme voor ![]() wordt gegeven door Rabinowitz en Wagon (1995; Borwein en Bailey 2003, pp. 141-142).
wordt gegeven door Rabinowitz en Wagon (1995; Borwein en Bailey 2003, pp. 141-142).
Nog verbazingwekkender is de ontdekking door Bailey et al. van een gesloten vormexpressie die een cijfer-extractie-algoritme geeft dat cijfers van ![]() (of
(of ![]() ) in basis-16 oplevert (Bailey et al. (Bailey et al. 1997, Adamchik and Wagon 1997),
) in basis-16 oplevert (Bailey et al. (Bailey et al. 1997, Adamchik and Wagon 1997),
|
(30)
|
Deze formule, bekend als de BBP-formule, werd ontdekt met behulp van het PSLQ-algoritme (Ferguson et al. 1999) en is equivalent aan
|
(31)
|
Er is een serie BBP-type formules voor ![]() in machten van
in machten van ![]() , waarvan de eerste paar onafhankelijke formules zijn
, waarvan de eerste paar onafhankelijke formules zijn
|
(32)
|
|||
|
(33)
|
|||
|
(34)
|
|||
 |
(35)
|
||
 |
(36)
|
||
 |
(37)
|
Zo zijn er ook een reeks BBP-type formules voor ![]() in machten van
in machten van ![]() , waarvan de eerste paar onafhankelijke formules zijn
, waarvan de eerste paar onafhankelijke formules zijn
|
(38)
|
|||
|
(39)
|
|||
 |
(40)
|
||
 |
(41)
|
||
 |
(42)
|
||
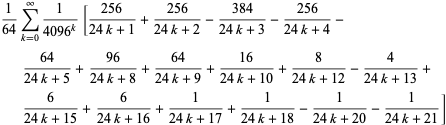 |
(43)
|
||
 |
(44)
|
||
 |
(45)
|
||
 |
(46)
|
||
 |
(47)
|
||
 |
(48)
|
F. Bellard vond de snel convergerende BBP-typeformule
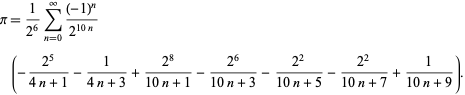 |
(49)
|
Een verwante integraal is
|
(50)
|
(Dalzell 1944, 1971; Le Lionnais 1983, p. 22; Borwein, Bailey, and Girgensohn 2004, p. 3; Boros and Moll 2004, p. 125; Lucas 2005; Borwein et al. 2007, p. 14). Deze integraal was bekend bij K. Mahler in het midden van de jaren 1960 en komt voor in een examen aan de Universiteit van Sydney in november 1960 (Borwein, Bailey, and Girgensohn, p. 3). Beukers (2000) en Boros en Moll (2004, p. 126) stellen dat het niet duidelijk is of er een natuurlijke keuze bestaat van een rationale polynoom waarvan de integraal tussen 0 en 1 ![]() oplevert, waarbij 333/106 de eerstvolgende convergente is. Er bestaat echter een integraal voor de vierde convergente, namelijk
oplevert, waarbij 333/106 de eerstvolgende convergente is. Er bestaat echter een integraal voor de vierde convergente, namelijk
|
(51)
|
(Lucas 2005; Bailey et al. 2007, p. 219). Lucas (2005) geeft nog een paar van dergelijke integralen.
Backhouse (1995) gebruikte de identiteit
|
(52)
|
|||
|
(53)
|
|||
|
(54)
|
voor positieve gehele getallen ![]() en
en ![]() en waarbij
en waarbij ![]() ,
, ![]() , en
, en ![]() rationale constante zijn om een aantal formules voor
rationale constante zijn om een aantal formules voor ![]() te genereren. In het bijzonder, als
te genereren. In het bijzonder, als ![]() , dan is
, dan is ![]() (Lucas 2005).
(Lucas 2005).
Een soortgelijke formule werd later ontdekt door Ferguson, wat leidt tot een tweedimensionaal rooster van dergelijke formules die kunnen worden gegenereerd door deze twee formules, gegeven door
|
(55)
|
voor elke complexe waarde van ![]() (Adamchik en Wagon), wat de BBP-formule geeft als het speciale geval
(Adamchik en Wagon), wat de BBP-formule geeft als het speciale geval ![]() .
.
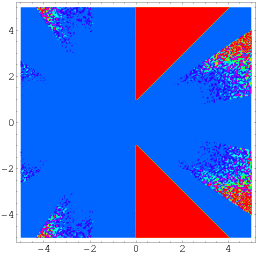
Een nog algemenere identiteit door Wagon wordt gegeven door
 |
(56)
|
(Borwein en Bailey 2003, p. 141), die geldt voor een gebied van het complexe vlak met uitzondering van twee driehoekige delen die symmetrisch om de reële as zijn geplaatst, zoals hierboven is geïllustreerd.
Een wellicht nog algemenere klasse van identiteiten wordt gegeven door
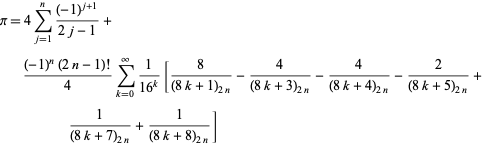 |
(57)
|
die geldt voor elk positief geheel getal ![]() , waarbij
, waarbij ![]() een Pochhammer-symbool is (B. Cloitre, pers. comm., 23 jan. 2005). Nog verbazingwekkender is dat er een nauw verwante formule is voor de natuurlijke logaritme van 2.
een Pochhammer-symbool is (B. Cloitre, pers. comm., 23 jan. 2005). Nog verbazingwekkender is dat er een nauw verwante formule is voor de natuurlijke logaritme van 2.
Na de ontdekking van de BBP-formule met 16 basisgetallen en verwante formules, werden soortgelijke formules in andere basisgetallen onderzocht. Borwein, Bailey, en Girgensohn (2004) hebben onlangs aangetoond dat ![]() geen Machin-type BBP arctangent formule heeft die niet binair is, hoewel dit niet uitsluit dat er een geheel ander schema is voor cijfer-extractie algoritmen in andere grondslagen.
geen Machin-type BBP arctangent formule heeft die niet binair is, hoewel dit niet uitsluit dat er een geheel ander schema is voor cijfer-extractie algoritmen in andere grondslagen.
S. Plouffe heeft een algoritme bedacht om het ![]() de cijfer van
de cijfer van ![]() in elke basis te berekenen in
in elke basis te berekenen in ![]() stappen.
stappen.
Een reeks aanvullende identiteiten door Ramanujan, Catalan, en Newton worden gegeven door Castellanos (1988ab, pp. 86-88), waaronder een aantal met betrekking tot sommen van Fibonacci getallen. Ramanujan vond
 |
(58)
|
(Hardy 1923, 1924, 1999, p. 7).
Plouffe (2006) vond de mooie formule
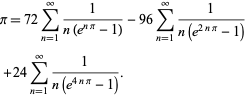 |
(59)
|
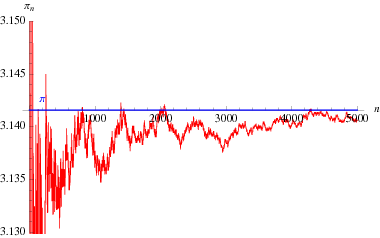
Een interessante oneindige productformule van Euler die ![]() en het
en het ![]() e priemgetal
e priemgetal ![]() met elkaar in verband brengt is
met elkaar in verband brengt is
 |
(60)
|
||
|
(61)
|
(Blatner 1997, p. 119), hierboven uitgezet als functie van het aantal termen in het product.
Een soortgelijke methode als die van Archimedes kan worden gebruikt om ![]() te schatten door te beginnen met een
te schatten door te beginnen met een ![]() -gon en dan de oppervlakte van de daaropvolgende
-gon en dan de oppervlakte van de daaropvolgende ![]() -gons te relateren. Stel
-gons te relateren. Stel ![]() is de hoek vanaf het middelpunt van een van de segmenten van de veelhoek,
is de hoek vanaf het middelpunt van een van de segmenten van de veelhoek,
|
(62)
|
dan
|
(63)
|
(Beckmann 1989, pp. 92-94).
Vieta (1593) was de eerste die een exacte uitdrukking gaf voor ![]() door
door ![]() te nemen in bovenstaande uitdrukking, die
te nemen in bovenstaande uitdrukking, die
|
(64)
|
wat leidt tot een oneindig product van geneste rradicalen,
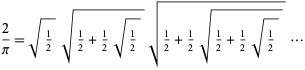 |
(65)
|
(Wells 1986, p. 50; Beckmann 1989, p. 95). Van deze uitdrukking werd echter pas in 1892 door Rudio rigoureus bewezen dat ze convergeert.
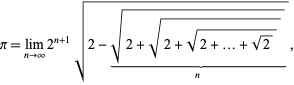
Een verwante formule wordt gegeven door
 |
(66)
|
die kan worden geschreven
|
(67)
|
waar ![]() is gedefinieerd met behulp van de iteratie
is gedefinieerd met behulp van de iteratie
 |
(68)
|
met ![]() (J. Munkhammar, pers. comm, 27 april 2000). De formule
(J. Munkhammar, pers. comm, 27 april 2000). De formule
 |
(69)
|
is ook nauw verwant.
Een mooie formule voor ![]() wordt gegeven door
wordt gegeven door
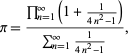 |
(70)
|
waar de teller een vorm is van de Wallis formule voor ![]() en de noemer een telescopische som met som 1/2 aangezien
en de noemer een telescopische som met som 1/2 aangezien
|
(71)
|
(Sondow 1997).
Een bijzonder geval van de Wallis-formule geeft
|
(72)
|
(Wells 1986, p. 50). Deze formule kan ook worden geschreven
 |
(73)
|
waar ![]() een binomiaal coëfficiënt aanduidt en
een binomiaal coëfficiënt aanduidt en ![]() de gammafunctie is (Knopp 1990). Euler verkreeg
de gammafunctie is (Knopp 1990). Euler verkreeg
|
(74)
|
hetgeen volgt uit de speciale waarde van de Riemann zeta-functie ![]() . Soortgelijke formules volgen uit
. Soortgelijke formules volgen uit ![]() voor alle positieve gehele getallen
voor alle positieve gehele getallen ![]() .
.
Een oneindige som door Ramanujan is
|
(75)
|
(Borwein et al. 1989; Borwein and Bailey 2003, p. 109; Bailey et al.2007, p. 44). Verdere sommen worden gegeven in Ramanujan (1913-14),
|
(76)
|
en
|
(77)
|
|||
|
(78)
|
(Beeler et al. 1972, punt 139; Borwein et al. 1989; Borwein en Bailey 2003, p. 108; Bailey et al. 2007, p. 44). Vergelijking (78) is afgeleid van een modulaire identiteit van orde 58, hoewel een eerste afleiding niet werd voorgesteld vóór Borwein en Borwein (1987). De bovenstaande reeksen geven beide
|
(79)
|
(Wells 1986, p. 54) als eerste benadering en geven respectievelijk ongeveer 6 en 8 decimalen per term. Dergelijke reeksen bestaan vanwege de rationaliteit van diverse modulaire invarianten.
De algemene vorm van de reeks is
|
(80)
|
waar ![]() een binaire kwadratische vormdiscriminant is,
een binaire kwadratische vormdiscriminant is, ![]() is de j-functie,
is de j-functie,
|
(81)
|
|||
|
(82)
|
en de ![]() zijn Eisensteinreeksen. Een klassegetal
zijn Eisensteinreeksen. Een klassegetal ![]() veld bevat
veld bevat ![]() de graad algebraïsche gehele getallen van de constanten
de graad algebraïsche gehele getallen van de constanten ![]() ,
, ![]() , en
, en ![]() . Van alle reeksen die alleen uit gehele termen bestaan, komt de reeks die in de kortste tijd de meeste numerieke cijfers geeft overeen met de grootste discriminant van klasse nummer 1,
. Van alle reeksen die alleen uit gehele termen bestaan, komt de reeks die in de kortste tijd de meeste numerieke cijfers geeft overeen met de grootste discriminant van klasse nummer 1, ![]() , en werd geformuleerd door de gebroeders Chudnovsky (1987). De 163 die hier voorkomt is dezelfde die voorkomt in het feit dat
, en werd geformuleerd door de gebroeders Chudnovsky (1987). De 163 die hier voorkomt is dezelfde die voorkomt in het feit dat ![]() (de constante van Ramanujan) zeer dicht bij een geheel getal ligt. Evenzo komt de factor
(de constante van Ramanujan) zeer dicht bij een geheel getal ligt. Evenzo komt de factor ![]() uit de j-gelijkvormigheid voor
uit de j-gelijkvormigheid voor ![]() . De reeks wordt gegeven door
. De reeks wordt gegeven door
|
(83)
|
|||
|
(84)
|
(Borwein en Borwein 1993; Beck en Trott; Bailey et al. 2007, p. 44). Deze reeks geeft 14 cijfers nauwkeurig per term. Dezelfde vergelijking in een andere vorm is gegeven door de gebroeders Chudnovsky (1987) en wordt door de Wolfram Language gebruikt om ![]() te berekenen (Vardi 1991; Wolfram Research),
te berekenen (Vardi 1991; Wolfram Research),
|
(85)
|
waar
|
(86)
|
|||
|
(87)
|
|||
|
(88)
|
De beste formule voor klasse nummer 2 (grootste discriminant ![]() ) is
) is
|
(89)
|
waar
|
(90)
|
|||
|
(91)
|
|||
|
(92)
|
(Borwein en Borwein 1993). Deze reeks telt ongeveer 25 cijfers op voor elke extra term. De snelst convergerende reeks voor klasse nummer 3 komt overeen met ![]() en geeft 37-38 cijfers per term. De snelst convergerende reeks voor klasse nummer 4 komt overeen met
en geeft 37-38 cijfers per term. De snelst convergerende reeks voor klasse nummer 4 komt overeen met ![]() en is
en is
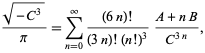 |
(93)
|
waar
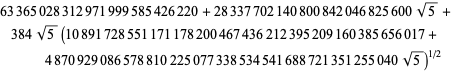 |
(94)
|
||
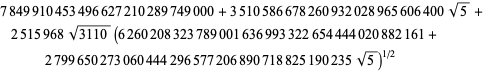 |
(95)
|
||
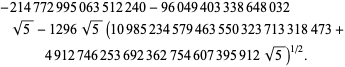 |
(96)
|
Dit geeft 50 cijfers per term. Borwein en Borwein (1993) hebben een algemeen algoritme ontwikkeld voor het genereren van dergelijke reeksen voor willekeurige klassen.
Een volledige lijst van Ramanujans reeksen voor ![]() die in zijn tweede en derde notitieboek zijn gevonden, wordt gegeven door Berndt (1994, pp. 352-354),
die in zijn tweede en derde notitieboek zijn gevonden, wordt gegeven door Berndt (1994, pp. 352-354),
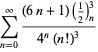 |
(97)
|
||
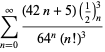 |
(98)
|
||
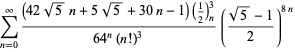 |
(99)
|
||
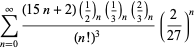 |
(100)
|
||
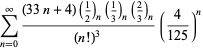 |
(101)
|
||
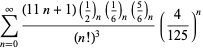 |
(102)
|
||
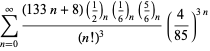 |
(103)
|
||
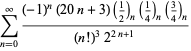 |
(104)
|
||
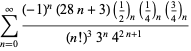 |
(105)
|
||
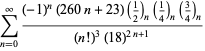 |
(106)
|
||
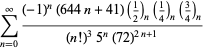 |
(107)
|
||
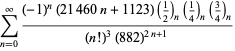 |
(108)
|
||
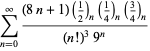 |
(109)
|
||
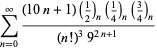 |
(110)
|
||
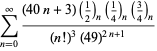 |
(111)
|
||
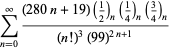 |
(112)
|
||
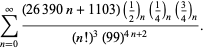 |
(113)
|
Deze vergelijkingen zijn voor het eerst bewezen door Borwein en Borwein (1987a, pp. 177-187). Borwein en Borwein (1987b, 1988, 1993) bewezen andere vergelijkingen van dit type, en Chudnovsky en Chudnovsky (1987) vonden soortgelijke vergelijkingen voor andere transcendentale constanten (Bailey et al. 2007, pp. 44-45).
Een volledige lijst van onafhankelijke bekende vergelijkingen van dit type wordt gegeven door
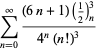 |
(114)
|
||
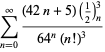 |
(115)
|
||
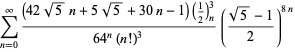 |
(116)
|
||
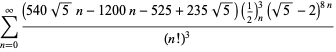 |
(117)
|
||
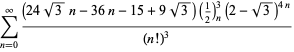 |
(118)
|
voor ![]() met niet-alternatieve tekens,
met niet-alternatieve tekens,
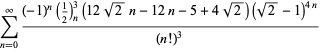 |
(119)
|
||
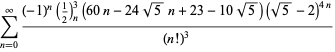 |
(120)
|
||
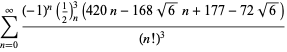 |
(121)
|
||
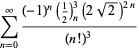 |
(122)
|
voor ![]() met wisselende tekens,
met wisselende tekens,
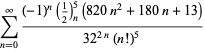 |
(123)
|
||
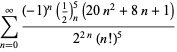 |
(124)
|
voor ![]() (Guillera 2002, 2003, 2006),
(Guillera 2002, 2003, 2006),
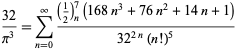 |
(125)
|
voor ![]() (Guillera 2002, 2003, 2006), en geen andere voor
(Guillera 2002, 2003, 2006), en geen andere voor ![]() zijn bekend (Bailey et al. 2007, pp. 45-48).
zijn bekend (Bailey et al. 2007, pp. 45-48).
Bellard geeft de exotische formule
 |
(126)
|
where
|
(127)
|
Gasper citeert het resultaat
|
(128)
|
waar ![]() een gegeneraliseerde hypergeometrische functie is, en transformeert deze tot
een gegeneraliseerde hypergeometrische functie is, en transformeert deze tot
|
(129)
|
Een fascinerend resultaat van Gosper wordt gegeven door
|
(130)
|
![]() voldoet aan de ongelijkheid
voldoet aan de ongelijkheid
|
(131)
|
D. Terr (pers. comm.) merkte de merkwaardige identiteit op
|
(132)
|
in verband met de eerste 9 cijfers van pi.