Rotatiekinematica - Natuurkunde 298

“Men praat over het doden van de tijd, terwijl de tijd hen stilletjes doodt”
Dion Boucicault – London Assurance (1841)

Tot nu toe hebben we de kinematica en dynamica van deeltjes beschouwd, met inbegrip van translatorische en cirkelvormige bewegingen, alsook de translatorische beweging van stelsels van deeltjes (in het bijzonder starre lichamen) in termen van de beweging van het massamiddelpunt van het stelsel (lichaam). In het laatste geval kunnen wij ons voorstellen dat alle massa van het voorwerp zich in het massamiddelpunt bevindt voor zover het externe translationele krachten betreft.

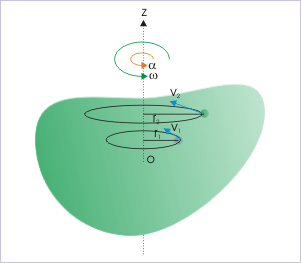De volgende stap is het beschouwen van de rotatie van een star lichaam om een vaste rotatieas. Merk op dat, omdat we een star lichaam beschouwen, elk deeltje in het lichaam vast blijft ten opzichte van de andere. Dit betekent dat in een dergelijke rotatiebeweging elk deeltje beweegt in een cirkel waarvan het middelpunt op de rotatieas ligt. In het diagram rechts roteert het voorwerp om de z-as; de twee proefdeeltjes bewegen in cirkels met stralen r1 en r2. Indien men de cirkelvormige beweging van een deeltje kan beschrijven, zonder directe verwijzing naar zijn straal, dan zullen alle deeltjes in het systeem beschreven worden door dezelfde verzameling vergelijkingen. Hoewel de stralen van de deeltjes verschillend zijn, zijn hun hoekverdraaiingen identiek. Daarom is het nodig om hoekvariabelen te introduceren.

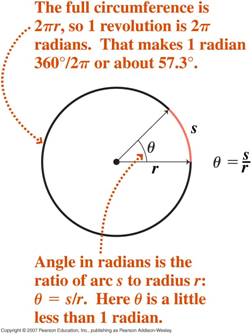
Radiale maat van hoeken

Hoeksnelheid (Speed) en hoekversnelling

Hoeksnelheid en hoekversnelling worden op soortgelijke wijze gedefinieerd als snelheid en versnelling. Er zijn gemiddelde en momentane waarden van elk.

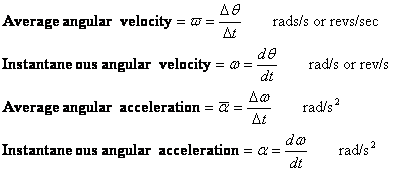
Hoekversnelling is niet hetzelfde als centripetale versnelling. Centripetale versnelling is het gevolg van een verandering in de richting van de snelheid, hoekversnelling is het gevolg van een verandering in de grootte van de snelheid (door de draaiingshoek).

Precies zoals in het translationele geval is het verschil tussen hoeksnelheid en hoeksnelheid de richting. Bij hoeksnelheid moet de draairichting om de as in kwestie worden vermeld. Bijvoorbeeld, 10 rad/s met de klok mee om de x-as is een hoeksnelheid, 10 rad/s om de x-as is een hoeksnelheid.

Rotationele kinematische vergelijkingen

Naar directe analogie met de translationele kinematische vergelijkingen kan de cirkelvormige beweging om één as onder constante hoekversnelling worden beschreven door de volgende vier vergelijkingen,

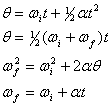
waarbij we de substituties hebben aangebracht,

Merk op dat net zoals +x willekeurig naar rechts kan worden gedefinieerd, de positieve waarde van theta kan worden gedefinieerd als met de klok mee of tegen de klok in.

Verband tussen hoek- en translatiegrootheden

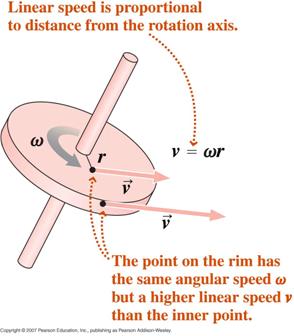Uitgaande van de definitie van de radiaalmaat kunnen we, door te differentiëren ten opzichte van de tijd, aantonen dat,

waar v de tangentiële snelheid is en a de tangentiële versnelling.

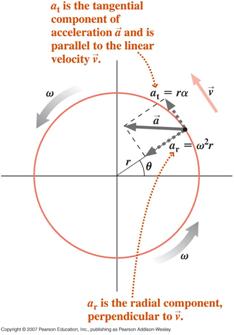
Een deeltje dat een cirkelvormige beweging uitvoert, met een variërende hoeksnelheid (niet-uniforme cirkelvormige beweging), zal twee componenten van versnelling ondervinden, een tangentiële component ten gevolge van de veranderende grootte van zijn snelheid en een radiale (centripetale) component ten gevolge van de veranderende richting van zijn snelheid

De netto versnelling van het deeltje is de vectorsom van deze twee componenten, zoals hieronder aangegeven.

Ter informatie…

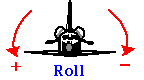
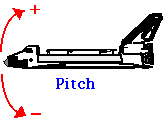
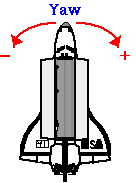
Gelijktijdige rotatie om meer dan één as kan worden beschouwd op een soortgelijke manier als projectielbeweging, waar we onze 1D translationele discussie hebben uitgebreid naar 2D beweging. In luchtvaarttoepassingen worden rotaties om de drie assen beschreven als Roll, Pitch en Yaw.