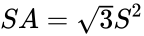Voor het wetenschappelijk tijdschrift, zie Tetrahedron (tijdschrift).
| Reguliere Tetraëder | |
|---|---|
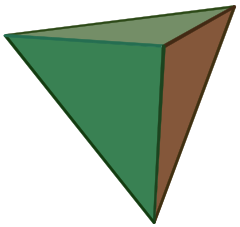 (Klik hier voor roterend model) |
|
| Type | Platonische vaste stof |
| Elementen | F = 4, E = 6 V = 4 (χ = 2) |
| Zijkanten | 4{3} |
| Schläfli symbool | {3,3} en s{2,2} |
| Wythoff-symbool | 3 | 2 3 | 2 2 2 |
| Coxeter-Dynkin | |
| Symmetrie | Td of (*332) |
| U01, C15, W1 | |
| Eigenschappen | Regelmatige convexe deltaëder |
| Dihedrale hoek | 70.528779° = arccos(1/3) |
 3.3.3 (hoekpuntfiguur) |
 Zelfduaal (duaal veelvlak) |
 Net |
|
Een tetraëder (meervoud: tetraëder) is een veelvlak dat bestaat uit vier driehoekige zijvlakken, waarvan er drie bij elk hoekpunt samenkomen. Een regelmatige tetraëder is een tetraëder waarbij de vier driehoeken regelmatig, of “gelijkzijdig” zijn, en is een van de Platonische vaste lichamen.
De tetraëder is een soort piramide, dat is een veelvlak met een vlakke veelhoekige basis en driehoekige vlakken die de basis verbinden met een gemeenschappelijk punt. Bij een tetraëder is het grondvlak een driehoek (elk van de vier zijvlakken kan als grondvlak worden beschouwd), zodat een tetraëder ook wel driehoekige piramide of deltaëder wordt genoemd.
Formules voor regelmatige tetraëder
Het volume is
De oppervlakte is
Template:Commonscat
- F. M. Jackson en Weisstein, Eric W., “Tetrahedron” van MathWorld.
- Weisstein, Eric W., “Tetrahedron” uit MathWorld.
- Weisstein, Eric W., “Tetrahedron” uit MathWorld.
- De Uniforme Veelvlakken
- Tetrahedron: Interactive Polyhedron Model
- K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Piero della Francesca’s formule voor het volume van een tetraëder bij MathPages
- Gratis papieren modellen van een tetraëder en vele andere veelvlakken
- Een verbazingwekkende, Ruimtevullende, Niet-regelmatige Tetraëder die ook een beschrijving bevat van een “roterende ring van tetraëders”, ook bekend als een caleidocyclus.
- Tetrahedron Core Network Toepassing van een tetraëderstructuur om een veerkrachtig partial-mesh datanetwerk te maken
- Expliciete exacte formules voor de traagheidstrekker van een willekeurig tetraëder in termen van zijn hoekpuntcoördinaten
- De traagheidstrekker van een tetraëder