
Wiskunde behandelt een enorm aantal concepten die erg belangrijk zijn, maar tegelijkertijd ook complex en tijdrovend. Python biedt echter de volwaardige SciPy-bibliotheek die dit probleem voor ons oplost. In deze SciPy-tutorial leert u hoe u deze bibliotheek kunt gebruiken, samen met een paar functies en hun voorbeelden.
Voordat u verder gaat, bekijkt u eerst alle onderwerpen die in dit artikel zijn besproken:
- Wat is SciPy?
- NumPy vs SciPy
- Subpackages in SciPy
- Basisfuncties
- Speciale functies
- Integratiefuncties
- Optimalisatiefuncties
- Fourier Transform-functies
- Signaal Processing Functions
- Linear Algebra
- Sparse Eigenvalues
- Spatial Data Structures and Algorithms
- Multidimensional Image Processing Functions
- File IO
Dus laten we maar eens beginnen. 🙂
SciPy is een open-source Python bibliotheek die wordt gebruikt om wetenschappelijke en wiskundige problemen op te lossen. Het is gebouwd op de NumPy extensie en stelt de gebruiker in staat om gegevens te manipuleren en te visualiseren met een breed scala aan high-level commando’s. Zoals eerder vermeld, bouwt SciPy voort op NumPy en daarom is het niet nodig om NumPy te importeren als je SciPy importeert.
NumPy vs SciPy
Zowel NumPy als SciPy zijn Python bibliotheken die worden gebruikt voor wiskundige en numerieke analyse. NumPy bevat array-gegevens en basisbewerkingen zoals sorteren, indexeren, enz., terwijl SciPy alle numerieke code bevat. Hoewel NumPy een aantal functies biedt die kunnen helpen bij het oplossen van lineaire algebra, Fourier transformaties, enz., is SciPy de bibliotheek die eigenlijk volledig uitgeruste versies van deze functies bevat, samen met vele andere. Als u echter wetenschappelijke analyses uitvoert met Python, moet u zowel NumPy als SciPy installeren, aangezien SciPy voortbouwt op NumPy.
Subpackages in SciPy:
SciPy heeft een aantal subpackages voor diverse wetenschappelijke berekeningen die in de volgende tabel zijn weergegeven:

Maar voor een gedetailleerde beschrijving kunt u de officiële documentatie volgen.
Deze pakketten moeten uitsluitend worden geïmporteerd voordat u ze kunt gebruiken. Bijvoorbeeld:
from scipy import cluster
Voordat we elk van deze functies in detail bekijken, kijken we eerst naar de functies die zowel in NumPy als in SciPy voorkomen.
Interactie met NumPy:
SciPy bouwt voort op NumPy en daarom kunt u gebruik maken van NumPy-functies zelf om met arrays om te gaan. Om meer over deze functies te weten te komen, kun je simpelweg gebruik maken van de functies help(), info() of source().
help():
Om informatie over een functie te krijgen, kun je gebruik maken van de functie help(). Er zijn twee manieren waarop deze functie kan worden gebruikt:
- zonder parameters
- met parameters
Hier volgt een voorbeeld dat beide bovenstaande methoden laat zien:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
Wanneer u de bovenstaande code uitvoert, geeft de eerste help() de informatie over de clustersubmodule. De tweede help() vraagt de gebruiker om de naam van een module, sleutelwoord, enz. in te voeren waarvoor de gebruiker informatie wenst te zoeken. Om de uitvoering van deze functie te stoppen, typt u simpelweg ‘quit’ en drukt u op enter.
info():
Deze functie retourneert informatie over de gewenste functies, modules, etc.
scipy.info(cluster)
source():
De broncode wordt alleen geretourneerd voor objecten die in Python zijn geschreven. Deze functie retourneert geen nuttige informatie indien de methoden of objecten zijn geschreven in een andere taal zoals C. Indien u echter gebruik wilt maken van deze functie, kunt u dat als volgt doen:
scipy.source(cluster)
Speciale functies:
SciPy biedt een aantal speciale functies die worden gebruikt in de wiskundige natuurkunde, zoals elliptische, gemaksfuncties, gamma, beta, enz. Om te zoeken naar alle functies, kunt u gebruik maken van help() functie zoals eerder beschreven.
Exponentiële en Trigonometrische Functies:
SciPy’s Special Function pakket biedt een aantal functies waarmee je exponenten kunt vinden en trigonometrische problemen kunt oplossen.
Bedenk het volgende voorbeeld:
EXAMPLE:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
OUTPUT:
1000,0
8,0
1,0
0.7071067811865475
Er zijn nog veel meer functies aanwezig in het speciale functies pakket van SciPy die u zelf kunt proberen.
Integratie Functies:
SciPy biedt een aantal functies om integralen op te lossen. Variërend van gewone differentiaalintegrator tot het gebruik van trapeziumregels om integralen te berekenen, SciPy is een opslagplaats van functies om alle soorten integralenproblemen op te lossen.
Algemene integratie:
SiPy biedt een functie met de naam quad om de integraal van een functie met één variabele te berekenen. De grenzen kunnen ( ) zijn om oneindige grenzen aan te geven. De syntaxis van de functie quad() is als volgt:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1,49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Hier wordt de functie geïntegreerd tussen de grenzen a en b (kan ook oneindig zijn).
EXAMPLE:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
In het bovenstaande voorbeeld wordt de functie ‘a’ geëvalueerd tussen de grenzen 0, 1. Wanneer deze code wordt uitgevoerd, ziet u de volgende uitvoer.
OUTPUT:
(3,9086503371292665, 4,3394735994897923e-14)
Double Integral Function:
SciPy biedt dblquad dat kan worden gebruikt om dubbele integralen te berekenen. Een dubbele integraal, zoals velen van ons weten, bestaat uit twee reële variabelen. De functie dblquad() neemt de te integreren functie als parameter samen met 4 andere variabelen die de limieten en de functies dy en dx definiëren.
EXAMPLE:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
OUTPUT:
-1.333333333335, 1.4802973661668755e-14)
SciPy biedt verschillende andere functies om drievoudige integralen, n-integralen, Romberg-integralen, enz. te evalueren die u verder in detail kunt onderzoeken. Om alle details over de vereiste functies te vinden, gebruikt u de helpfunctie.
Optimalisatiefuncties:
De scipy.optimize biedt een aantal veelgebruikte optimalisatiealgoritmen die kunnen worden bekeken met behulp van de helpfunctie.
Het bestaat in principe uit het volgende:
- Onbeperkt en beperkt minimaliseren van multivariate scalaire functies, d.w.z. minimaliseren (bijv. BFGS, Newton Conjugate Gradient, Nelder_mead simplex, enz)
- Globale optimaliseringsroutines (bijv. differential_evolution, dual_annealing, enz)
- Laatste-kwadraten-minimalisatie en krommingsaanpassing (bijv. least_squares, curve_fit, enz)
- Scalaire univariate functies-minimalisatoren en wortelzoekers (bijv. minimize_scalar en root_scalar)
- Multivariate vergelijkingssysteem oplossers met behulp van algoritmen zoals hybride Powell, Levenberg-Marquardt.
Rosenbrook Functie:
Rosenbrook functie ( rosen) is een testprobleem dat wordt gebruikt voor gradient-gebaseerde optimalisatie algoritmen. Het is als volgt gedefinieerd in SciPy:

EXAMPLE:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
OUTPUT: 7371.0399999999945
Nelder-Mead:
De methode Nelder-Mead is een numerieke methode die vaak wordt gebruikt om de min/max van een functie in een multidimensionale ruimte te vinden. In het volgende voorbeeld wordt de methode minimize samen met het Nelder-Mead-algoritme gebruikt.
VOORBEELD:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
OUTPUT: array()
Interpolatiefuncties:
In het vakgebied van de numerieke analyse verwijst interpolatie naar het construeren van nieuwe gegevenspunten binnen een verzameling bekende gegevenspunten. De SciPy-bibliotheek bestaat uit een subpackage met de naam scipy.interpolate dat bestaat uit spline-functies en -klassen, eendimensionale en multidimensionale (univariate en multivariate) interpolatieklassen, enz.
Univariate interpolatie:
Univariate interpolatie is in feite een gebied van curve-fitting dat de kromme vindt die een exacte fit geeft aan een reeks van tweedimensionale datapunten. SciPy biedt de functie interp1d die kan worden gebruikt om univariate interpolatie te produceren.
EXAMPLE:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
OUTPUT:
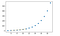
Multivariate interpolatie:
Multivariate interpolatie (ruimtelijke interpolatie ) is een soort interpolatie op functies die uit meer dan één variabelen bestaan. Het volgende voorbeeld toont een voorbeeld van de
Interpolatie over een 2-D-raster met behulp van de functie interp2d(x, y, z) In principe worden x, y, z-arrays gebruikt om een of andere functie interp2d-functie te benaderen. f: “z = f(x, y)” en geeft een functie terug waarvan de aanroepmethode spline-interpolatie gebruikt om de waarde van nieuwe punten te vinden.
VOORBEELD:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
OUTPUT:

Fourier Transform Functies:
Fourier analyse is een methode die zich bezighoudt met het uitdrukken van een functie als een som van periodieke componenten en het terugwinnen van het signaal uit die componenten. De fft-functies kunnen worden gebruikt om de discrete fouriertransformatie van een reële of complexe reeks terug te geven.
VOORBEELD:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
OUTPUT:
Ook hiervan kunt u de inverse vinden door de ifft-functie als volgt te gebruiken:
VOORBEELD:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
OUTPUT:
Signaalverwerkingsfuncties:
Signaalverwerking houdt zich bezig met het analyseren, wijzigen en synthetiseren van signalen zoals geluid, beelden, enz. SciPy biedt een aantal functies waarmee u eendimensionale en tweedimensionale gegevens kunt vormgeven, filteren en interpoleren.
Filtering:
Door een signaal te filteren, verwijdert u in feite ongewenste componenten uit het signaal. Om een geordende filtering uit te voeren, kunt u gebruik maken van de functie order_filter. Deze functie voert in principe een geordende filtering uit op een matrix. De syntaxis van deze functie is als volgt:
SYNTAX:
order_filter(a, domain, rank)
a = N-dimensionale invoer-array
domain = masker-array met hetzelfde aantal dimensies als `a`
rank = Niet-negatief getal dat elementen uit de lijst selecteert nadat deze is gesorteerd (0 is de kleinste, gevolgd door 1…)
VOORBEELD:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
Waveforms:
Het scipy.signal subpackage bestaat ook uit verschillende functies die kunnen worden gebruikt om golfvormen te genereren. Eén zo’n functie is chirp. Deze functie is een frequentie-gewuifde cosinusgenerator en de syntaxis is als volgt:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)
waar,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
OUTPUT:

Lineaire algebra:
Lineaire algebra houdt zich bezig met lineaire vergelijkingen en hun representaties met behulp van vectorruimten en matrices. SciPy is gebouwd op ATLAS LAPACK en BLAS bibliotheken en is extreem snel in het oplossen van problemen met betrekking tot lineaire algebra. Naast alle functies uit numpy.linalg, biedt scipy.linalg ook een aantal andere geavanceerde functies. Ook als numpy.linalg niet samen met ATLAS LAPACK en BLAS ondersteuning wordt gebruikt, is scipy.linalg sneller dan numpy.linalg.
Vinden van de inverse van een matrix:
Mathematisch gezien is de inverse van een matrix A de matrix zodanig dat waar de identiteitsmatrix is bestaande uit enen langs de hoofddiagonaal, aangeduid als B=A-1. In SciPy kan deze inverse worden verkregen met de methode linalg.inv.
EXAMPLE:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
OUTPUT:
]
De determinanten vinden:
De rekenkundig afgeleide waarde van de coëfficiënten van de matrix staat bekend als de determinant van een vierkante matrix. In SciPy kan dit worden gedaan met een functie det die de volgende syntaxis heeft:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
waar,
a : (M, M) een vierkante matrix is
overwrite_a( bool, optioneel) : Sta het overschrijven van gegevens in a toe
check_finite ( bool, optioneel): Om te controleren of de ingevoerde matrix alleen uit eindige getallen bestaat
EXAMPLE:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
OUTPUT: -5.0
Sparse Eigenwaarden:
Eigenwaarden zijn een specifieke verzameling van scalaren die gekoppeld zijn aan lineaire vergelijkingen. ARPACK biedt de mogelijkheid om eigenwaarden ( eigenvectoren ) vrij snel te vinden. De volledige functionaliteit van ARPACK is verpakt in twee high-level interfaces die scipy.sparse.linalg.eigs en scipy.sparse.linalg.eigsh. eigs zijn. Met de eigs interface kunnen de eigenwaarden van reële of complexe niet-symmetrische vierkante matrices worden gevonden, terwijl de eigsh interface interfaces bevat voor reëel-symmetrische of complex-hermitische matrices.
De eigh functie lost een veralgemeend eigenwaarde probleem op voor een complexe Hermitische of reële symmetrische matrix.
EXAMPLE:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
OUTPUT:
Geselecteerde eigenwaarden :
Complexe ndarray :
]
Spatiale datastructuren en algoritmen:
Spatiale gegevens bestaan in wezen uit objecten die zijn opgebouwd uit lijnen, punten, oppervlakken, enz. Het scipy.spatial pakket van SciPy kan Voronoi-diagrammen, triangulaties, enz. berekenen met behulp van de Qhull-bibliotheek. Het bestaat ook uit KDTree implementaties voor nearest-neighbor point queries.
Delaunay triangulaties:
Mathematisch gezien is een Delaunay triangulatie voor een verzameling discrete punten in een vlak een triangulatie zodanig dat geen enkel punt in de gegeven verzameling punten binnen de omtrek van enige driehoek ligt.
VOORBEELD:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
OUTPUT:

Multidimensionale beeldbewerkingsfuncties:
Beeldbewerking houdt zich in feite bezig met het uitvoeren van bewerkingen op een beeld om informatie te verkrijgen of om een verbeterd beeld te krijgen van het oorspronkelijke beeld. Het pakket scipy.ndimage bestaat uit een aantal beeldverwerkings- en analysefuncties die zijn ontworpen om te werken met matrices van willekeurige dimensionaliteit.
Convolutie en correlatie:
SciPy biedt een aantal functies die correlatie en convolutie van beelden mogelijk maken.
- De functie correlate1d kan worden gebruikt om eendimensionale correlatie langs een gegeven as te berekenen
- De functie correlate maakt multidimensionale correlatie van een gegeven matrix met de gespecificeerde kernel mogelijk
- De functie convolve1d kan worden gebruikt om eendimensionale convolutie langs een gegeven as te berekenen
- De functie convolve kan worden gebruikt om eendimensionale convolutiedimensionale convolutie langs een gegeven as te berekenen
- De functie convolve maakt multidimensionale convolutie van een willekeurige matrix met de opgegeven kernel mogelijk
EXAMPLE:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
OUTPUT: array()
Bestand IO:
Het scipy.io pakket biedt een aantal functies die u helpen bestanden van verschillende formaten te beheren, zoals MATLAB-bestanden, IDL-bestanden, Matrix Market-bestanden, enz.
Om gebruik te maken van dit pakket, moet u het als volgt importeren:
import scipy.io as sio
Voor volledige informatie over het subpakket, kunt u het officiële document over File IO raadplegen.
Dit brengt ons aan het einde van deze SciPy Tutorial. Ik hoop dat u alles duidelijk hebt begrepen. Zorg ervoor dat u zo veel mogelijk oefent.
Als u meer artikelen wilt bekijken over de meest trending technologieën van de markt, zoals Artificial Intelligence, DevOps, Ethical Hacking, dan kunt u verwijzen naar de officiële site van Edureka.
Zoek uit naar andere artikelen in deze serie die de verschillende andere aspecten van Python en Data Science zullen uitleggen.
1. Machine Learning Classifier in Python
2. Python Scikit-Learn Cheat Sheet
3. Machine Learning Tools
4. Python Bibliotheken Voor Data Wetenschap En Machine Leren
5. Chatbot In Python
6. Python Collecties
7. Python Modules
8. Python Ontwikkelaars Vaardigheden
9. OOPs Interview Vragen en Antwoorden
10. C.V. Voor Een Python Ontwikkelaar
11. Verkennende Gegevensanalyse In Python
12. Slangenspel met Python’s Turtle Module
13. Python Ontwikkelaar Salaris
14. Principale Componenten Analyse
15. Python vs C++
16. Scrapy-handleiding
17. Web Scraping met Python
18. Minst kwadraten regressie methode
19. Jupyter notitieboek spiekbriefje
20. Python Grondbeginselen
21. Python Patroonprogramma’s
22. Generatoren in Python
23. Python Decorator
24. Python Spyder IDE
25. Mobiele toepassingen met Kivy in Python
26. Top 10 beste boeken om & Python te leren
27. Robot Framework Met Python
28. Snake Game in Python met behulp van PyGame
29. Django Interview Vragen en Antwoorden
30. Top 10 Python Toepassingen
31. Hash Tables en Hashmaps in Python
32. Python 3.8
33. Support Vector Machine
34. Python handleiding