Cómo preparar las preguntas de geometría en un examen de matemáticas
Información general
La geometría es sólo un nombre elegante para el estudio de las líneas y las formas. Ciertamente hay principios y temas difíciles adicionales, pero aquí tenemos lo básico. Tendrá que dominar estos antes de abordar conceptos más avanzados.
(Tenga en cuenta que si una figura está etiquetada como «ejemplo» en esta guía, puede no ser la única representación de esa figura, pero es una de ellas.)
Puntos y líneas
Un punto en geometría es un lugar. No tiene longitud, anchura ni profundidad. Utilizamos un punto y una letra mayúscula para mostrar un punto.
Un segmento de línea está definido por dos puntos y todos los puntos entre ellos. Los dos puntos se llaman puntos extremos del segmento. Un segmento tiene una dimensión: la longitud. Para escribir un segmento, se coloca una barra sobre los dos puntos extremos. \(\sobrelínea{AB}) o \(\sobrelínea{BA}) es este segmento:

Una línea se extiende en ambas direcciones sin fin. Para escribir una línea, se coloca una barra con dos flechas sobre dos puntos cualesquiera de la línea. \(\sobreflecha izquierda derecha{AB}}) o \(\sobreflecha izquierda derecha{BA}} es la línea:

Una semirrecta comienza en un punto final y se extiende sin fin en una sola dirección. Para escribir una semirrecta, se coloca una barra con una flecha apuntando a la derecha sobre dos puntos: el punto final y cualquier otro punto (en esa dirección). \(\sobreflechaderecha{AB}) es la semirrecta:

Nota: no se puede escribir una semirrecta con la flecha apuntando a la izquierda como \(\sobreflechaizquierda{BA}). Además, el orden es importante. \ (\ sobre flecha derecha{BA}) no es lo mismo que \ (\ sobre flecha derecha{AB}). La primera letra es siempre el punto de partida de una semirrecta.
Dos líneas, segmentos o semirrectas son perpendiculares si forman un ángulo recto (ver más abajo). Utilice el símbolo \(\perp\) para denotar la perpendicularidad. Por ejemplo, si \(\sobrelínea{AB}) es perpendicular a \(\sobrelínea{CD}\), se puede escribir \(\sobrelínea{AB}\perp \sobrelínea{CD}\).
Ejemplos: 
Dos líneas son paralelas si nunca se cruzan. Si \(\overleftrightarrow{AB}) es paralela a \(\overleftrightarrow{CD}), se puede escribir \(\overleftrightarrow{AB} \parallel \overleftrightarrow{CD}).
Ejemplos: 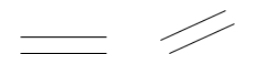
Formas planas
En geometría, un plano es una superficie plana bidimensional que se extiende infinitamente. Las dos dimensiones son la longitud y la anchura. Por tanto, las formas planas son formas «planas», como los cuadrados, los círculos y los triángulos.
Formas comunes
Un polígono es una superficie cerrada en un plano limitada por segmentos de línea llamados lados.
Ejemplos: 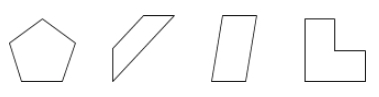
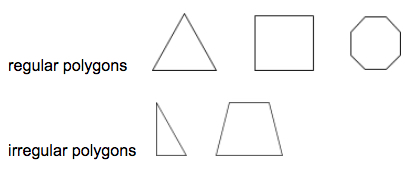
Un polígono regular es un polígono en el que todos los segmentos y ángulos interiores son congruentes.
Ejemplos:
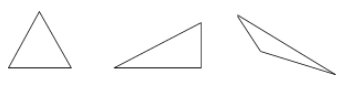
Un triángulo es un polígono de tres lados.
Ejemplos:
Los cuadriláteros – polígonos de cuatro lados
Un paralelogramo es un tipo de cuadrilátero donde los lados opuestos son paralelos y congruentes. Los ángulos opuestos de un paralelogramo también son congruentes.
Ejemplos: 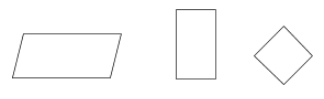
Un rectángulo es un paralelogramo con cuatro ángulos rectos.
Ejemplos: 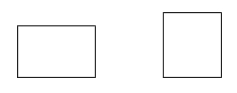
Un rombo es un paralelogramo en el que los cuatro lados son congruentes.
Ejemplos: 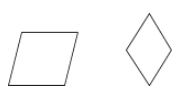
Un cuadrado es un paralelogramo que es a la vez un rombo y un rectángulo (todos los lados son congruentes y todos los ángulos son rectos).
Ejemplos: 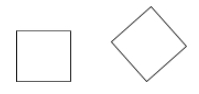
Un trapezoide es un cuadrilátero con un solo par de lados paralelos.
Ejemplos: 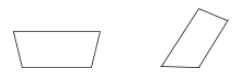
Polígonos con más de cuatro lados
\
(^1\) Un polígono con 11 lados también puede llamarse endecágono o undecágono.
Medición de formas
El perímetro es la distancia total alrededor de un polígono. Para hallar el perímetro, basta con sumar las longitudes de todos los lados. Si el polígono es regular (todos los lados son congruentes) y la longitud de un lado es \(s\), entonces multiplica el número de lados por \(s\) para encontrar el perímetro. Por ejemplo, el perímetro de un pentágono regular es \(P_\text{reg pentágono}=5s\)