AC, lub prąd zmienny, jest tak nazwany, ponieważ prąd zmienia się lub przerzuca się tam i z powrotem pomiędzy dwoma biegunami. Innymi słowy, prąd (a co za tym idzie napięcie) jest funkcją czasu. Jest to zasadnicza różnica w porównaniu z prądem stałym, który jest stały pod względem biegunowości i generalnie niezmienny w czasie. Na przykład laboratoryjne źródło napięcia stałego idealnie utrzymuje ustalone napięcie na swoich zaciskach i nie zmienia się w czasie. W przeciwieństwie do tego, gdy przebieg prądu przemiennego kołysze się w przód i w tył w czasie, jego kształt może wykazywać szerokie wahania, od prostych, regularnych ścieżek standardów laboratoryjnych, takich jak fale sinusoidalne, trójkątne i kwadratowe, do znacznie bardziej złożonych i falujących przebiegów wytwarzanych przez instrumenty muzyczne i głos ludzki.
Fala sinusoidalna jest najprostszą falą, jaką można utworzyć. Reprezentuje ona ruch prostego wektora obracającego się ze stałą prędkością, takiego jak pionowe przesunięcie wskazówki sekundowej zegara. Przykład jest pokazany na rysunku \(\PageIndex{1}). Na osi poziomej zaznaczono czas. Wzrasta ona wraz z przesuwaniem się od lewej do prawej (tzn. jeśli punkt A znajduje się na prawo od punktu B, to A występuje później w czasie niż B). Oś pionowa jest tu przedstawiona jako procent maksimum, ale zwykle jest to pomiar napięcia, natężenia prądu, ciśnienia akustycznego lub podobnych wielkości.
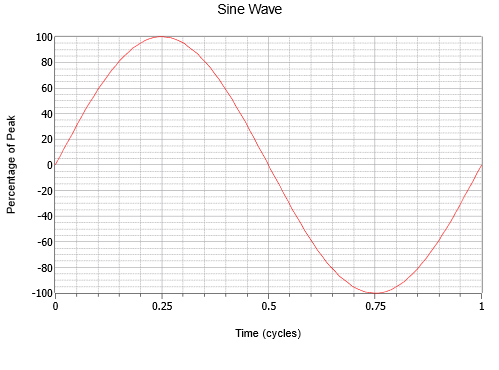
Rysunek 1: Sinusoida.
Zauważ płynną zmienność, która zaczyna się od zera, wznosi się do dodatniego szczytu jedną czwartą drogi, spada z powrotem do zera w połowie drogi, kontynuuje do ujemnego szczytu trzy czwarte drogi, a następnie wznosi się ponownie do miejsca, w którym się zaczęła. Proces ten następnie powtarza się. Każde powtórzenie jest określane jako cykl. Na rysunku pokazano jeden pełny cykl.
Fale sinusoidalne wykazują symetrię ćwierćfalową. Oznacza to, że każda ćwiartka (w czasie) fali jest identyczna z każdą inną, jeśli po prostu obrócimy ją wokół osi poziomej i/lub obrócimy pionowo wokół jej szczytu. Czas potrzebny do wykonania jednego cyklu nazywany jest okresem i oznaczany jest symbolem T (od ang. Time). Odwrotnością okresu jest częstotliwość, \(f\).
Częstotliwość wskazuje, ile cykli istnieje w jednej sekundzie. Aby uhonorować jednego z XIX-wiecznych badaczy w tej dziedzinie, zamiast nazywać tę jednostkę „cyklami na sekundę”, używamy Hertzów, nazwanych tak od nazwiska Heinricha Hertza i oznaczanych skrótem Hz. Na rysunku przedstawiono trzy sinusoidy o różnych częstotliwościach; falę początkową (zielona), falę o dwukrotnie wyższej częstotliwości (niebieska) i trzecią o połowie częstotliwości lub dwukrotnie dłuższym okresie (czerwona).
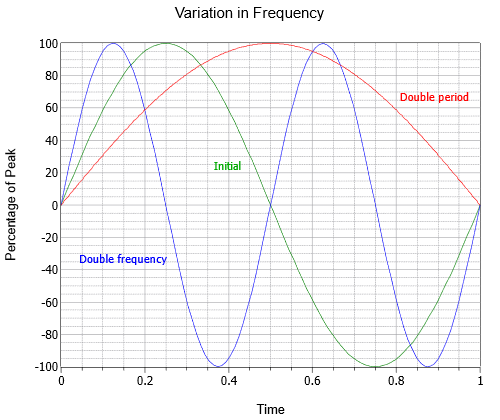
Rysunek \(\): Zmienność częstotliwości sinusoidy.
Amplituda (pionowa) fali może być wyrażona jako wielkość szczytowa, która jest zmianą od środkowej linii zerowej aż do najbardziej dodatniej wartości. Amplituda może być również wyrażona jako peak-to-peak; odległość od najbardziej ujemnej do najbardziej dodatniej wartości. Dla fali sinusoidalnej będzie to zawsze dwukrotność wartości szczytowej, chociaż może to nie dotyczyć innych fal, które mogą być asymetryczne. Seria trzech fal sinusoidalnych o różnych amplitudach jest pokazana na rysunku. Obok początkowej (zielonej) znajdują się wersje o podwójnej amplitudzie (niebieska) i połowie amplitudy (czerwona).
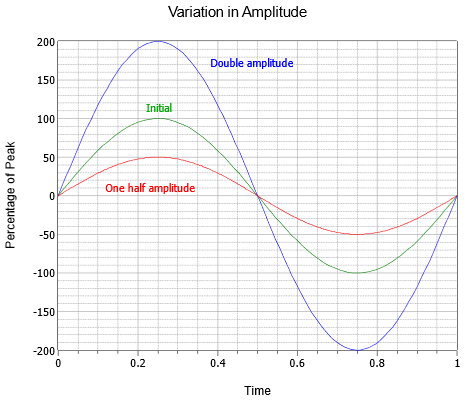
Rysunek \(\PageIndex{3}}): Zmienność amplitudy sinusoidy.
Połączenie tych parametrów, rozważmy przebieg napięcia pokazany na rysunku \(\PageIndex{4}). Widzimy tu dwa cykle fali napięcia przemiennego.
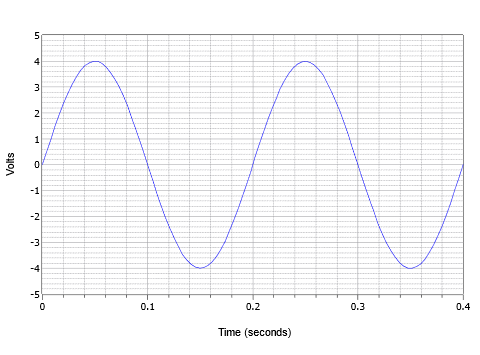
Rysunek \(\PageIndex{4}}): Przykład podstawowej fali sinusoidalnej.
Wartość szczytowa wynosi 4 wolty, a wartość międzyszczytowa 8 woltów (zwykle oznaczana skrótem „8 V pp”). Okres jednego cyklu wynosi 0,2 sekundy, lub T = 200 milisekund. Dalej, częstotliwość, \(f = 1/200\) milisekund, lub 5 Hz (5 cykli w jednej sekundzie).
Fale AC mogą być również łączone z przesunięciem DC. Dodanie dodatniego poziomu DC przesuwa falę w górę pionowo, podczas gdy ujemny poziom DC przesuwa falę w dół pionowo. Nie zmienia to częstotliwości ani części AC amplitudy (chociaż absolutne wartości szczytowe przesuną się o wartość DC). Rysunek pokazuje efekt różnych przesunięć DC. Powyżej fali początkowej (zielony) znajduje się identyczna fala z dodatnim przesunięciem DC równym 20% oryginalnej wartości szczytowej (niebieski). Poniżej oryginału znajduje się trzecia fala (czerwona), która wykazuje ujemne przesunięcie DC równe połowie wartości szczytowej oryginału.
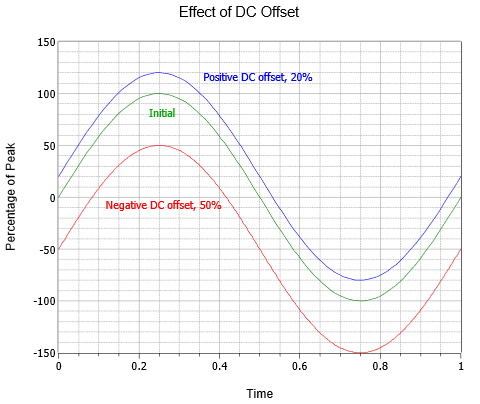
Rysunek \(\): Sinusoidalna zmiana przesunięcia DC.
Dalej, możliwe jest, aby sinusoida była przesunięta w czasie w stosunku do jakiejś innej sinusoidy lub odniesienia. Chociaż możliwe jest wskazanie tego przesunięcia jako czasu bezwzględnego, bardziej powszechne jest robienie tego jako przesunięcie fazowe, to jest czas wyrażony jako część okresu w stopniach. Na przykład, jeśli jeden sinus wyprzedza drugi o jedną czwartą okresu, to mówi się, że prowadzi o 90 (tj. 1/4 z 360). Jeśli jest opóźniony o ½ okresu, mówi się, że jest opóźniony o 180 (tj. jest późniejszy w czasie o 1/2 cyklu). Innym sposobem wyrażenia tego jest to, że wiodące przebiegi zaczynają się wcześniej w czasie i dlatego są rysowane na lewo od odniesienia, podczas gdy opóźnione przebiegi zaczynają się później w czasie i są rysowane na prawo.
Rysunek \(\PageIndex{6}}) ilustruje efekt przesunięcia fazowego. Zauważ, że w tym wykresie krzywa (t = 0) została przesunięta do środka osi poziomej. Środkowa krzywa to fala początkowa lub referencyjna (zielona). Po lewej stronie (czerwona) znajduje się fala poprzedzająca falę początkową o jedną ósmą cyklu, czyli 45. Po prawej stronie (niebieska), znajduje się fala opóźniona o połowę, czyli -22,5 cyklu.
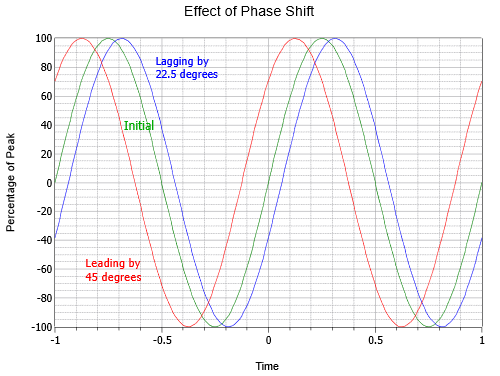
Rysunek \(\): Zmienność fazy sinusoidy.
Połączenie powyższych elementów pozwala nam na opracowanie ogólnego formatu sinusoidy (pokazano napięcie):
Gdzie
(v(t)\) jest napięciem w pewnym czasie \(t),
(V_{DC}) jest przesunięciem DC, jeśli istnieje,
(V_{P}) jest wartością szczytową,
(f) to częstotliwość,
(itha) to przesunięcie fazowe (+ jeśli jest wiodące i rysowane w lewo, – jeśli jest opóźnione i rysowane w prawo).
Dla szybkiego i praktycznego przykładu, przebieg pokazany na rysunku ma amplitudę 4 V, częstotliwość 5 Hz i nie ma przesunięcia DC ani przesunięcia fazowego. Zatem jego wyrażenie to \(v(t) = 4 \sin (2 \pi 5 t)\)
Aby obliczyć przesunięcie fazowe, najpierw określ różnicę czasu między przebiegiem a odniesieniem, które nazwiemy \(Delta t\). Odniesieniem może być stały punkt w czasie (np. \(t = 0\)) lub inny przebieg. Ogólnie rzecz biorąc, łatwym sposobem jest zmierzenie różnicy na przecięciach zerowych, zakładając, że nie ma offsetu DC. Jeśli występuje przesunięcie, należy wykonać pomiar w miejscu, do którego przesunięto przejście zerowe (tj. na poziomie przesunięcia DC). Gdy różnica zostanie znaleziona, podziel ją przez okres, aby przedstawić przesunięcie jako ułamek okresu. Ponieważ jeden cykl reprezentuje jeden obrót wektora, czyli 360 stopni, wystarczy pomnożyć ułamek przez 360 stopni, aby znaleźć przesunięcie fazowe w stopniach. Wyrażone jako wzór:
Pamiętaj, jeśli fala jest przesunięta w lewo to jest wiodąca i pozytywna, podczas gdy przesunięcie w prawo jest opóźnione lub opóźnione w czasie, a więc negatywne.
Przykład
Zapisz wyrażenie dla fali przedstawionej na rysunku
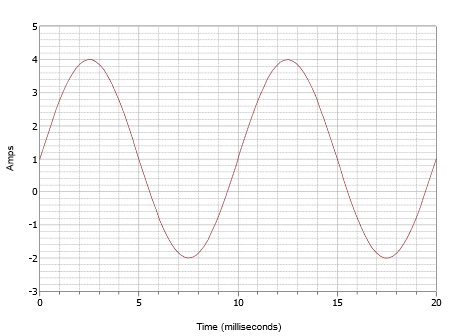
Ryc: Waveform for Example \(\PageIndex{1}\).
Ten przebieg powierzchownie może wyglądać jak ten na rysunku \(\PageIndex{4}), ale nie daj się zwieść. Przede wszystkim, skala czasowa jest inna. W przypadku tego przebiegu jeden cykl kończy się w ciągu 10 milisekund. Dlatego częstotliwość wynosi
Drugą kwestią jest przesunięcie DC. Zauważ, że dodatni szczyt występuje przy 4 amperach, podczas gdy ujemny szczyt występuje przy -2 amperach. Wskazuje to na wartość peak-topeak równą 6 amperów. Bez offsetu, dodatni szczyt byłby przy 3 amperach, dlatego jest +1 amper offsetu DC. Pionowy środek przebiegu jest przesunięty w górę od 0 amperów do +1 ampera. Punkt ten znajduje się w t = 0, dlatego nie ma przesunięcia fazowego. Otrzymane wyrażenie ma postać:
Przykład
Zapisz wyrażenie dla przebiegu przedstawionego na rysunku
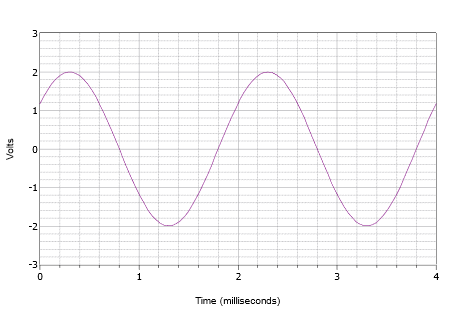
Rysunek
Przykład 
Rysunek 
Przykład  : Waveform for Example \(\PageIndex{2}\).
: Waveform for Example \(\PageIndex{2}\).
Po pierwsze, dodatni szczyt wynosi 2 V, a wartość międzyszczytowa to 4 V. Dlatego nie ma przesunięcia DC. Pionowy środek fali nie zaczyna się w punkcie \(t = 0\), zatem musi wystąpić przesunięcie fazowe. Wartość w punkcie t = 0 wynosi 1,2 V. Fala osiąga tę samą amplitudę w chwili \(t = 2) milisekundy i zaczyna powtarzać kolejny cykl. W związku z tym okres musi wynosić 2 milisekundy. Częstotliwość jest odwrotnością tej wartości, a zatem \(f = 500\) Hz.
Forma fali jest przesunięta w lewo, co wskazuje na dodatnie lub wiodące przesunięcie fazowe. Jeśli zbadamy drugi cykl, widzimy, że trafia na zero woltów w 1,8 milisekundy. Dlatego przesunięcie wynosi 0,2 milisekundy. Wyrażone w stopniach jest to:
Końcowe wyrażenie jest następujące:
Przykład:
Narysuj przebieg odpowiadający poniższemu wyrażeniu.
Po pierwsze zauważ, że przesunięcie o -3 V powoduje obniżenie wartości szczytowej dodatniej z 5 V do 2 V, a wartości szczytowej ujemnej z -5 V do -8 V. Częstotliwość 40 kHz dyktuje okres:
Przesunięcie fazowe wynoszące -72 odpowiada 72/360, czyli 0,2 cyklu. Odpowiada to opóźnieniu czasowemu (przesuniętemu w prawo, ponieważ jest ujemne) równemu 0,2 razy 25 \u0026apos; lub 5 \u0026apos;
Na początku często najlepiej jest skonstruować wykres poprzez serię dyskretnych kroków, zamiast próbować narysować całość za jednym razem. Najpierw narysuj sinusoidę o amplitudzie szczytowej 5 V i okresie 25 Ω. Teraz przesuń przebieg o 3 wolty w dół, tak aby dodatni szczyt wynosił tylko 2 wolty, a ujemny szczyt -8 woltów. Na koniec przesuń nowo przesunięty przebieg w prawo o 5 V. Wynik jest pokazany na rysunku
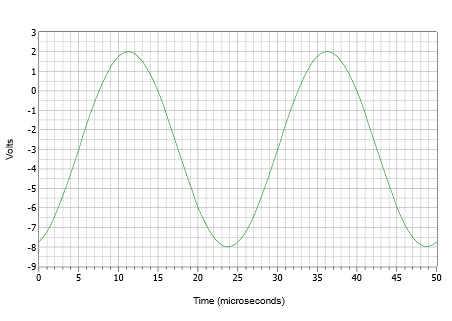
Ryc: Waveform for Example \(\PageIndex{3}\).
1.2.1: Pomiary laboratoryjne
W laboratorium, generator funkcyjny jest używany do generowania sinusów i innych kształtów fal. Urządzenia te pozwalają na precyzyjną kontrolę zarówno amplitudy jak i częstotliwości fali wraz z dodaniem offsetu DC, jeśli jest to pożądane. Przykład jest pokazany na rysunku \(\PageIndex{10}\). Odpowiednim narzędziem pomiarowym jest oscyloskop, lub po prostu scope, w skrócie.

Rysunek \(\PageIndex{10}}): Laboratoryjny generator sygnału.
Oscyloskop jest prawdopodobnie najbardziej użytecznym i wszechstronnym urządzeniem pomiarowym w laboratorium. Zazwyczaj posiada dwa lub cztery kanały wejściowe, choć możliwe jest zastosowanie większej ich liczby. Każdy kanał wejściowy ma swoją własną regulację czułości, a wszystkie kanały mają wspólne odniesienie czasowe. Wyświetlacz rysuje przebiegi w taki sam sposób, jak na rysunkach \(\PageIndex{1}} – \(\PageIndex{9}}. Mogą one również wykreślać jedno napięcie w stosunku do drugiego (tryb X – Y). Nowoczesne oscyloskopy posiadają dodatkowe funkcje, takie jak automatyczny pomiar częstotliwości, amplitudy, przesunięcia fazowego itp., pomiary z użyciem kursora oraz możliwość zapisywania wyświetlanych obrazów jako plików graficznych. Przykład czterokanałowego oscyloskopu cyfrowego pokazano na rysunku

Rysunek \(\): Oscyloskop cyfrowy.
1.2.2: Symbole schematów
Jeśli chodzi o schematy, symbole źródeł napięcia i prądu zmiennego są pokazane na rysunku \(\PageIndex{12}}). Oznaczenia biegunowości i kierunku nie są bezwzględne; w końcu są to źródła prądu przemiennego, których biegunowość i kierunek zmieniają się w przód i w tył. Zamiast tego znaczniki są używane do ustanowienia odniesienia czasowego, szczególnie w obwodach wykorzystujących wiele źródeł.
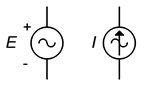
Rysunek \(\PageIndex{12}}): Symbole schematyczne źródła napięciowego AC (po lewej) i źródła prądowego (po prawej).
Warto pamiętać, że negacja źródła jest tym samym co odwrócenie jego polaryzacji. Było to prawdą dla źródeł prądu stałego i pozostaje prawdą dla źródeł prądu zmiennego. Jest to zilustrowane na rysunku \(\PageIndex{13}). Czasami odwrócenie lub zanegowanie źródła sprawi, że analiza będzie nieco bardziej oczywista lub łatwiejsza do zwizualizowania.
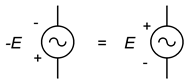
Rysunek \(\PageIndex{13}}): Równoważność biegunowości/znaku.
Przykład \(\PageIndex{4})
Załóżmy, że oscyloskop wyświetla dwie fale przedstawione na rysunku \(\PageIndex{14}). Wyznaczyć przesunięcie fazowe mniejszej fali o wartości szczytowej 20 V (niebieskiej) w stosunku do większej fali o wartości szczytowej 25 V (czerwonej).
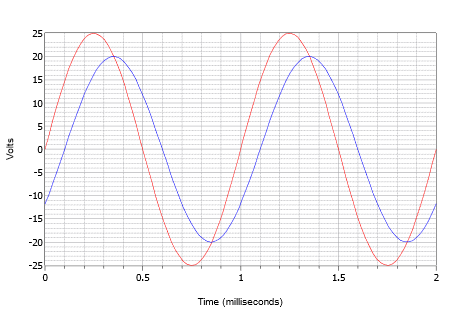
Rysunek \(\PageIndex{14}}): Przebiegi dla przykładu \(\PageIndex{4}).
Po pierwsze, zauważ, że żadna z fal nie wykazuje przesunięcia DC. Gdyby jedna lub obie miały przesunięcie, fale musiałyby być przesunięte w pionie tak, aby ich normalne punkty przecięcia zera były na tym samym poziomie. Mierząc którąkolwiek z fal, okazuje się, że okres wynosi 1 milisekundę. Przesunięcie czasowe najłatwiej znaleźć na którymkolwiek z punktów przecięcia zera (do wyboru są cztery miejsca). Opóźnienie wynosi jedno małe odchylenie, lub 0,1 milisekundy, przy czym mniejsza fala jest opóźniona w czasie, lub opóźniona w stosunku do większej fali. Oznacza to ujemne przesunięcie fazowe.
1.2.3: Sinus i cosinus
Istnieje garść specyficznych przesunięć fazowych, którym warto się bliżej przyjrzeć. Jeśli sinusoida jest odwrócona, to znaczy odwrócona do góry nogami, jest nie do odróżnienia od sinusoidy, która została przesunięta o +180 lub -180 stopni. Innymi słowy, taką falę można zapisać na trzy różne sposoby: \(- \sinus (2 \pi ft)\), \(\sinus (2 \pi ft – 180^{crc})\), lub \(\sinus (2 \pi ft + 180^{crc})\). Ponadto, jeżeli fala sinusoidalna jest przesunięta o +90 stopni (tj. do przodu i w lewo), może być również określana jako fala kosinusoidalna. Zatem \(\sin (2 \pi ft + 90^{circ}) = \ cos (2 \pi ft)\). Wreszcie, jeżeli sinusoida jest przesunięta o -90 stopni (tzn. opóźniona i w prawo), można ją określić jako ujemną lub odwróconą sinusoidę. Tak więc \(\sin (2 \pi ft – 90^{circ}) = – \cos (2 \pi ft)\). Zależności między tymi czterema falami ilustruje rysunek
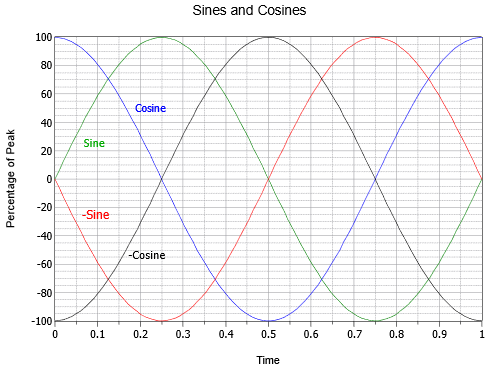
Rysunek
: Zależności czasowe między sinusami i cosinusami.
Warto również zauważyć, że fala cosinusowa reprezentuje pierwszą pochodną, lub nachylenie, fali sinusoidalnej. Jak być może pamiętasz z innych badań, nachylenie lub „stromość” linii jest stosunkiem zmiany pionowej do zmiany poziomej, czasami nazywanym „wzrostem nad biegiem”. W przypadku napięcia jest to zmiana napięcia w stosunku do zmiany w czasie, czyli \(\Delta V/ \Delta t\). W przypadku gładkiej, stale zmieniającej się krzywej, takiej jak sinusoida, nachylenie w danym punkcie jest definiowane jako pierwsza pochodna, czyli w tym przypadku \(dv/dt\). Aby to zweryfikować wizualnie, zauważ, że najbardziej stroma część sinusoidy (zielona) jest tam, gdzie przecina ona zero amplitudy. Ponieważ sinus przecina zero przy ruchu dodatnim (w punkcie t = 0 lub t = 1 na rysunku), cosinus (niebieski) znajduje się w dodatnim punkcie szczytowym. Ponieważ sinus przekracza zero przy ruchu ujemnym (przy \(t = 0,5)), cosinus znajduje się w ujemnym punkcie szczytowym. Ponadto sinusoida jest płaska, a jej nachylenie wynosi zero przy dodatnim i ujemnym szczycie (odpowiednio przy \(t = 0,25) i \(t = 0,75)), a w tych momentach amplituda cosinusa również wynosi zero. Prawdą jest również, że sinusoida jest nachyleniem ujemnej kosinusoidy, ujemny kosinus jest nachyleniem ujemnej sinusoidy, a ujemna sinusoida jest nachyleniem kosinusa. Idąc w odwrotnym kierunku, możemy powiedzieć, że antypochodna (całka nieokreślona) sinusoidy jest sinusoidą, całka sinusoidy jest ujemną kosinusoidą itd. Zależności te okażą się najbardziej przydatne, gdy zwrócimy naszą uwagę na odpowiedź kondensatorów i cewek w obwodach prądu zmiennego.
1.2.4: RMS – Root Mean Square Measurement
Along with peak and peak-to-peak, amplitude may be given as an RMS (Root Mean Square) value. W rzeczywistości, jeśli wartość szczytowa lub międzyszczytowa nie jest określona, przyjmuje się, że pomiar jest RMS. RMS jest specjalnym sposobem obliczania ekwiwalentnej mocy prądu stałego (bardzo często spotykane np. w przypadku wzmacniaczy mocy audio). Innymi słowy, jeśli jesteśmy zainteresowani znalezieniem mocy w rezystorze, obliczenia muszą być wykonane przy użyciu wartości RMS dla napięcia lub prądu, a nie wartości szczytowych lub międzyszczytowych. W przeciwnym wypadku otrzymamy błędne moce. Jest to prawdziwe niezależnie od kształtu fali; czy jest to sinusoida, trójkąt czy złożone fale sygnałów muzycznych. Jeśli napięcie jest określone jako RMS, może być traktowane do obliczeń mocy tak samo jak napięcie stałe o równoważnej wielkości. Na przykład, sinusoida o wartości 1 V RMS spowoduje takie samo rozproszenie mocy i nagrzewanie się danego rezystora, jak 1 V DC. Z tego powodu, RMS jest czasami określany jako wartość efektywna (tj. efektywna wartość DC).
Nazwa root-mean-square opisuje proces określania wartości efektywnej. Po pierwsze, przypomnij sobie, że moc jest proporcjonalna do kwadratu napięcia lub prądu. Zatem naszym pierwszym krokiem będzie podniesienie do kwadratu kształtu fali wejściowej. Oczywiście, przebieg ten jest funkcją czasu i jego kwadrat da jakiś nowy kształt. W tym momencie musimy znaleźć średnią wartość tego nowego kształtu. Powód tego jest prosty, ale niekoniecznie oczywisty. Elementy elektryczne i elektroniczne mają masę, a więc nie nagrzewają się i nie stygną natychmiastowo. Wykazują one termiczną stałą czasową. W związku z tym reagują na średnią wartość wejściową w czasie. Chociaż możemy obliczyć pewien sposób „chwilowej mocy szczytowej” w pewnym określonym momencie w czasie, nie reprezentuje to równoważnej mocy DC. Po uzyskaniu średniej wartości tego kwadratowego kształtu fali, odpowiadająca jej wartość prądu stałego jest po prostu pierwiastkiem kwadratowym ze średniej. Wynikiem jest wartość ułamkowa pomiędzy zerem a jednym, która jest używana jako współczynnik skalujący, aby przekształcić wartość szczytową w wartość RMS. Wartość ta będzie unikalna dla konkretnego kształtu fali. Oznacza to, że wszystkie sinusy (niezależnie od fazy) mają ten sam współczynnik, wszystkie regularne fale trójkątne mają ten sam współczynnik, i tak dalej. Ponieważ zajmujemy się głównie sinusami, przyjrzyjmy się bliżej określaniu współczynnika RMS dla nich.
Zaczynamy od podstawowego wyrażenia dla fali sinusoidalnej bez przesunięcia DC lub przesunięcia fazowego i o amplitudzie równej jeden:
Pierwszym krokiem jest podniesienie tego kształtu fali do kwadratu. Użyteczna tożsamość trygonometryczna to
Zastosowanie jej do naszej fali daje:
To wyrażenie opisuje odwróconą falę kosinusową o podwójnej oryginalnej częstotliwości i połowie oryginalnej amplitudy, jadącą na przesunięciu DC równym jej wartości szczytowej. Innymi słowy, ujemny szczyt cosinusa jest równy zero, a dodatni szczyt jest równy 1. Następnym krokiem jest znalezienie średniej lub średniej wartości tego pośredniego wyniku. Średnia jest równa przesunięciu o 0,5. Może to być wizualizowane jako obszar powyżej przesunięcia idealnie wypełniający „dip” poniżej przesunięcia. Ostatnim krokiem jest wyciągnięcie pierwiastka kwadratowego z wartości średniej. Pierwiastek kwadratowy z 0,5 jest równy jeden nad pierwiastkiem kwadratowym z dwóch, lub około 0,707. Dlatego wartość RMS jest 0,707 razy większa od wartości szczytowej. Alternatywnie, można podzielić wartość szczytową przez pierwiastek kwadratowy z dwóch, czyli w przybliżeniu 1,414. Proces ten jest przedstawiony graficznie na rysunku
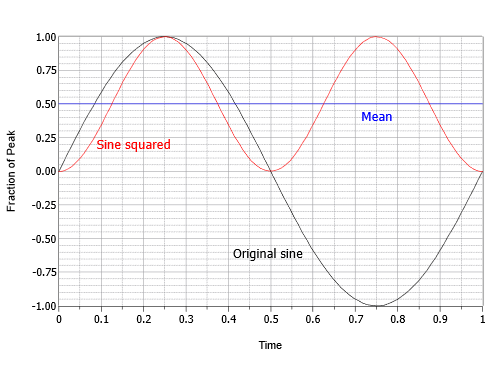
Rysunek \(\\): Proces znajdowania współczynnika RMS dla sinusoidy.
Podsumowując, dla sinusoidy, RMS jest zawsze wartością szczytową razy 0,707. Możemy również powiedzieć, że wartość RMS każdej fali sinusoidalnej jest jej wartością szczytową podzieloną przez około 1,414. Ponownie, te proporcje nie muszą być prawdziwe w przypadku fal niesinusoidalnych. Szczegóły dotyczące innych popularnych kształtów można znaleźć w dodatku C. Wreszcie, stosunek wartości szczytowej do wartości skutecznej nazywany jest współczynnikiem szczytu. Jest to stała wartość dla fal sinusoidalnych (ponownie, około 1,414), ale może być ponad 10:1 dla niektórych rodzajów sygnałów audio.
1.2.5: Długość fali
Innym elementem zainteresowania jest prędkość propagacji fali. Jest ona bardzo różna. W przypadku światła w próżni (lub w przybliżeniu, prądu elektrycznego w przewodzie), prędkość wynosi około 3E8 metrów na sekundę (tj. 300 000 km/s) lub około 186 000 mil na sekundę.
Dając prędkość i okres, możemy sobie wyobrazić, jak daleko od siebie znajdują się szczyty fali. Odległość ta nazywana jest długością fali i oznaczana jest grecką literą lambda (lambda). Długość fali jest równa prędkości podzielonej przez częstotliwość, ∙ (∙lambda = v/f). Tak więc, dla głośnika wytwarzającego sinusoidę o częstotliwości 100 Hz, jako że prędkość dźwięku w powietrzu wynosi 344 m/s, to ława = 344 m/s ława, / ława, 100) Hz, czyli 3,44 metra (nieco ponad 11 stóp). Zauważ, że im wyższa częstotliwość, tym krótsza długość fali. Zauważmy również, że im większa prędkość, tym większa długość fali. Obliczenia długości fali są szczególnie ważne w dziedzinie telekomunikacji i akustyki.
.