Wytrzymałość wiązań: Covalent Bonds
Stabilne cząsteczki istnieją, ponieważ wiązania kowalencyjne trzymają atomy razem. Miarą siły wiązania kowalencyjnego jest energia potrzebna do jego zerwania, czyli energia potrzebna do rozdzielenia połączonych atomów. Rozdzielenie jakiejkolwiek pary połączonych atomów wymaga energii; im silniejsze wiązanie, tym większa energia potrzebna do jego zerwania. Energia potrzebna do zerwania określonego wiązania kowalencyjnego w jednym molu cząsteczek gazu nazywana jest energią wiązania lub energią dysocjacji wiązania. Energia wiązania dla cząsteczki dwuatomowej, \(D_{X-Y}), jest zdefiniowana jako standardowa zmiana entalpii dla reakcji endotermicznej:
Na przykład, energia wiązania czystego kowalencyjnego wiązania H-H, \(delta_{H-H}), wynosi 436 kJ na mol zerwanego wiązania H-H:
Zerwanie wiązania zawsze wymaga dodania energii do cząsteczki. Odpowiednio, tworzenie wiązania zawsze uwalnia energię.
Cząsteczki z trzema lub więcej atomami mają dwa lub więcej wiązań. Suma energii wszystkich wiązań w takiej cząsteczce jest równa standardowej zmianie entalpii dla reakcji endotermicznej, która powoduje zerwanie wszystkich wiązań w cząsteczce. Na przykład, suma energii czterech wiązań C-H w CH4, 1660 kJ, jest równa standardowej zmianie entalpii reakcji:
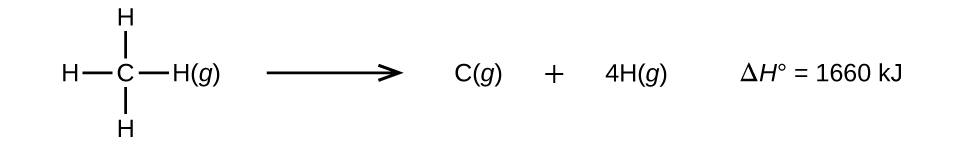
Średnia energia wiązania C-H, \(D_{C-H}), wynosi 1660/4 = 415 kJ/mol, ponieważ na mol reakcji przypadają cztery mole zerwanych wiązań C-H. Chociaż cztery wiązania C-H są równoważne w oryginalnej cząsteczce, nie wymagają one takiej samej energii do zerwania; po zerwaniu pierwszego wiązania (co wymaga 439 kJ/mol), pozostałe wiązania są łatwiejsze do zerwania. Wartość 415 kJ/mol jest średnia, a nie dokładna wartość wymagana do złamania każdego jednego bond.
Siła wiązania między dwoma atomami wzrasta wraz ze wzrostem liczby par elektronów w wiązaniu. Ogólnie rzecz biorąc, jak siła wiązania wzrasta, długość wiązania maleje. Tak więc, widzimy, że wiązania potrójne są silniejsze i krótsze niż wiązania podwójne między tymi samymi dwoma atomami; podobnie, wiązania podwójne są silniejsze i krótsze niż wiązania pojedyncze między tymi samymi dwoma atomami. Średnie energie wiązań dla niektórych typowych wiązań znajdują się w tabeli, a porównanie długości wiązań i sił wiązań dla niektórych typowych wiązań znajduje się w tabeli. Kiedy jeden atom łączy się z różnymi atomami w grupie, siła wiązania zazwyczaj maleje w miarę przesuwania się w dół grupy. Na przykład, C-F wynosi 439 kJ/mol, C-Cl wynosi 330 kJ/mol, a C-Br wynosi 275 kJ/mol.
| Bond | Bond Energy | Bond | Bond | Bond | Bond | Bond Energy | Bond Energy | |
|---|---|---|---|---|---|---|---|---|
| H-H | 436 | C-S | 260 | F-Cl | 255 | |||
| H-C | 415 | C-Cl | 330 | F-Br | 235 | |||
| H-N | 390 | C-Br | 275 | Si-Si | Si-Si | 230 | ||
| H-O | 464 | C-I | 240 | Si-P | 215 | |||
| H-F | 569 | N-N | 160 | Si-S | 225 | |||
| H-Si | 395 | N-N | 418 | Si-Cl | 359 | |||
| H-P | 320 | N-O | 200 | Si-Br | 290 | |||
| H-S | 340 | N-O | 200 | Si-I | 215 | |||
| H-Cl | 432 | N-F | 270 | P-P | 215 | |||
| H-Br | H-Br | 370 | N-P | 210 | P-S | 230 | ||
| H-I | 295 | N-Cl | 200 | P-Cl | 330 | |||
| C-C | 345 | N-Br | 245 | P-Br | 270 | |||
| C-C | 611 | O-O | O-O | 140 | P-I | 215 | ||
| (™athrm{C≡C}}) | 837 | (™athrm{O=O}}) | 498 | S-S | 215 | 215 | ||
| C-N | 290 | O-F | 160 | S-Cl | 250 | |||
| C-N | 615 | O-Si | 370 | S-Br | 215 | |||
| (™athrm{C≡N}}) | 891 | O-P | 350 | Cl-Cl | 243 | |||
| C-O | 350 | O-Cl | 205 | Cl-Br | 220 | |||
| C-O | 741 | O-I | 200 | 200 | Cl-I | 210 | ||
| C-F | 1080 | F-F | 160 | Br-Br | 190 | |||
| C-F | 439 | F-Si | 540 | Br-I | 180 | |||
| C-Si | 360 | F-P | 489 | I-I | 150 | |||
| C-P | 265 | F-S | 285 |
| Bond | Bond Length (Å) | Bond Energy (kJ/mol) |
|---|---|---|
| C-C | 1.54 | 345 |
| C-C | 1.34 | 611 |
| (™mathrm{C≡C}}) | 1.20 | 837 |
| C-N | 1.43 | 290 |
| (™mathrm{C=N}}) | 1.38 | 615 |
| (™mathrm{C≡N}}) | 1.16 | 891 |
| C-O | 1.43 | 350 |
| (™mathrm{C=O}}) | 1.23 | 741 |
| (™athrm{C≡O}}) | 1.13 | 1080 |
Energie wiązań możemy wykorzystać do obliczenia przybliżonych zmian entalpii dla reakcji, dla których entalpie tworzenia nie są dostępne. Obliczenia tego typu powiedzą nam również, czy reakcja jest egzotermiczna czy endotermiczna.
- Reakcja egzotermiczna (ΔH ujemne, ciepło wytworzone) zachodzi, gdy wiązania w produktach są silniejsze niż wiązania w reaktorach.
- Reakcja endotermiczna (ΔH dodatnie, ciepło pochłonięte) zachodzi, gdy wiązania w produktach są słabsze niż wiązania w reaktorach.
Zmiana entalpii, ΔH, dla reakcji chemicznej jest w przybliżeniu równa sumie energii wymaganej do zerwania wszystkich wiązań w reaktorach (energia „wejścia”, znak dodatni) plus energia uwolniona, gdy wszystkie wiązania są utworzone w produktach (energia „wyjścia”, znak ujemny). Można to wyrazić matematycznie w następujący sposób:
W tym wyrażeniu symbol \(\) oznacza „sumę”, a D oznacza energię wiązania w kilodżulach na mol, która zawsze jest liczbą dodatnią. Energię wiązania uzyskuje się z tabeli i zależy ona od tego, czy dane wiązanie jest wiązaniem pojedynczym, podwójnym czy potrójnym. Tak więc, przy obliczaniu entalpii w ten sposób, ważne jest, abyśmy wzięli pod uwagę wiązania we wszystkich reaktorach i produktach. Ponieważ wartości D są zazwyczaj wartościami średnimi dla jednego typu wiązania w wielu różnych cząsteczkach, obliczenia te dostarczają przybliżonych szacunków, a nie dokładnych wartości entalpii reakcji.
Rozważmy następującą reakcję:
lub
Aby utworzyć dwa mole HCl, należy rozerwać jeden mol wiązań H-H i jeden mol wiązań Cl-Cl. Energia potrzebna do rozerwania tych wiązań jest sumą energii wiązania H-H (436 kJ/mol) i wiązania Cl-Cl (243 kJ/mol). Podczas reakcji tworzą się dwa mole wiązań H-Cl (energia wiązania = 432 kJ/mol), uwalniając 2 × 432 kJ, czyli 864 kJ. Ponieważ wiązania w produktach są silniejsze niż te w reaktorach, reakcja uwalnia więcej energii niż zużywa:
-2D_{H-Cl}}}
&==mathrm{-2(432)=-185:kJ}
>końcówka {align*}}
Ta nadwyżka energii jest uwalniana w postaci ciepła, więc reakcja jest egzotermiczna. W tabeli T2 podano wartość standardowej molowej entalpii tworzenia się HCl(g), ΔH^, wynoszącą -92,307 kJ/mol. Dwukrotność tej wartości wynosi -184,6 kJ, co zgadza się z odpowiedzią uzyskaną wcześniej dla tworzenia się dwóch moli HCl.
Przykład \(\PageIndex{1}}): Using Bond Energies to Approximate Enthalpy Changes
Metanol, CH3OH, może być doskonałym paliwem alternatywnym. W wyniku wysokotemperaturowej reakcji pary wodnej i węgla powstaje mieszanina gazów: tlenku węgla (CO) i wodoru (H2), z której można wyprodukować metanol. Wykorzystując energie wiązań z tabeli, oblicz przybliżoną zmianę entalpii, ΔH, dla reakcji zachodzącej tutaj:
Roztwór
Najpierw musimy napisać struktury Lewisa reaktantów i produktów:
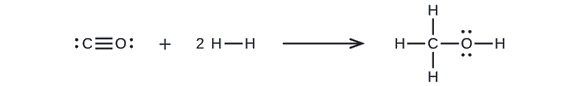
Z tego wynika, że ΔH dla tej reakcji obejmuje energię potrzebną do rozerwania potrójnego wiązania C-O i dwóch pojedynczych wiązań H-H, jak również energię wytworzoną przez utworzenie trzech pojedynczych wiązań C-H, pojedynczego wiązania C-O i pojedynczego wiązania O-H. Możemy to wyrazić następująco (poprzez równanie \ref{EQ3}):
}end {align*}]
Używając wartości energii wiązań w tabeli \(\PageIndex{2}), otrzymujemy:
=end {align*}]
Możemy porównać tę wartość z wartością obliczoną na podstawie danych ΔH^circ_ce f} z Dodatku G:
}end {align*}
Zauważ, że istnieje dość znaczna różnica pomiędzy wartościami obliczonymi za pomocą dwóch różnych metod. Dzieje się tak, ponieważ wartości D są średnią różnych sił wiązań; dlatego często dają one tylko przybliżoną zgodność z innymi danymi.
Ćwiczenie \(\PageIndex{1})
Alkohol etylowy, CH3CH2OH, był jednym z pierwszych organicznych związków chemicznych celowo zsyntetyzowanych przez człowieka. Ma wiele zastosowań w przemyśle i jest alkoholem zawartym w napojach alkoholowych. Może być otrzymywany przez fermentację cukru lub syntetyzowany przez hydratację etylenu w następującej reakcji:

Korzystając z energii wiązań w tabeli \), oblicz przybliżoną zmianę entalpii, ΔH, dla tej reakcji.
Podsumowanie
Wideo: Przegląd wiązań atomowych.
Wiązania kowalencyjne tworzą się, gdy elektrony są dzielone między atomy i są przyciągane przez jądra obu atomów. W czystych wiązaniach kowalencyjnych, elektrony są dzielone równo. W polarnych wiązaniach kowalencyjnych, elektrony są dzielone nierówno, ponieważ jeden atom wywiera silniejszą siłę przyciągania na elektrony niż drugi.
Siła wiązania kowalencyjnego jest mierzona jego energią dysocjacji wiązania, to jest ilością energii wymaganej do przerwania tego konkretnego wiązania w cząsteczce. Wiązania wielokrotne są silniejsze niż wiązania pojedyncze pomiędzy tymi samymi atomami. Entalpię reakcji można oszacować na podstawie nakładu energii wymaganej do zerwania wiązań i energii uwalnianej podczas tworzenia nowych wiązań.
Kluczowe równania
- Energia wiązania dla cząsteczki dwuatomowej: \(\ce{XY}(g)⟶\ce{X}(g)+\ce{Y}(g)\hspace{20px}\ce{D_{X–Y}}=ΔH°\)
- Enthalpy change: ΔH = ƩDbonds broken – ƩDbonds formed
Footnotes
- To pytanie pochodzi z Chemistry Advanced Placement Examination i zostało wykorzystane za zgodą Educational Testing Service.
Glossary
energia wiązania (także, energia dysocjacji wiązania) energia wymagana do zerwania wiązania kowalencyjnego w substancji gazowej
Kontrybutorzy
-
Paul Flowers (University of North Carolina – Pembroke), Klaus Theopold (University of Delaware) i Richard Langley (Stephen F. Austin State University) z autorami współpracującymi. Zawartość podręcznika wyprodukowana przez OpenStax College jest licencjonowana na licencji Creative Commons Attribution License 4.0. Pobierz za darmo na stronie http://cnx.org/contents/85abf193-2bd…[email protected]).
- Adelaide Clark, Oregon Institute of Technology
- Fuse School, Otwarte Zasoby Edukacyjne bezpłatnie, na licencji Creative Commons: Attribution-NonCommercial CC BY-NC (View License Deed: https://creativecommons.org/licenses/by-nc/4.0/)
- Crash Course Chemistry: Crash Course jest działem Complexly i filmy są wolne do strumienia dla celów edukacyjnych.
Feedback
Masz opinie do przekazania na temat tego tekstu? Kliknij tutaj.
Znalazłeś literówkę i chcesz uzyskać dodatkowe punkty? Kliknij tutaj.
.