
Matematyka zajmuje się ogromną liczbą pojęć, które są bardzo ważne, ale jednocześnie skomplikowane i czasochłonne. Jednakże Python dostarcza pełnowartościową bibliotekę SciPy, która rozwiązuje ten problem za nas. W tym tutorialu SciPy dowiesz się, jak korzystać z tej biblioteki wraz z kilkoma funkcjami i ich przykładami.
Zanim przejdziesz dalej, spójrz na wszystkie tematy omówione w tym artykule:
- Co to jest SciPy?
- NumPy vs SciPy
- Pakiety w SciPy
- Funkcje podstawowe
- Funkcje specjalne
- Funkcje całkujące
- Funkcje optymalizacyjne
- Funkcje transformacji Fouriera
- Funkcje przetwarzania sygnałów Processing Functions
- Linear Algebra
- Sparse Eigenvalues
- Spatial Data Structures and Algorithms
- Multidimensional Image Processing Functions
- File IO
Więc zaczynajmy. 🙂
SciPy jest open-source’ową biblioteką Pythona, która jest używana do rozwiązywania problemów naukowych i matematycznych. Jest ona zbudowana na rozszerzeniu NumPy i pozwala użytkownikowi na manipulowanie i wizualizację danych za pomocą szerokiej gamy poleceń wysokiego poziomu. Jak wspomniano wcześniej, SciPy opiera się na NumPy i dlatego jeśli importujesz SciPy, nie ma potrzeby importowania NumPy.
NumPy vs SciPy
Obie NumPy i SciPy są bibliotekami Pythona używanymi do analizy matematycznej i numerycznej. NumPy zawiera dane tablicowe i podstawowe operacje, takie jak sortowanie, indeksowanie, itp., podczas gdy SciPy składa się z całego kodu numerycznego. Chociaż NumPy zapewnia wiele funkcji, które mogą pomóc w rozwiązywaniu algebry liniowej, transformacji Fouriera itp, SciPy jest biblioteką, która faktycznie zawiera w pełni funkcjonalne wersje tych funkcji wraz z wieloma innymi. Jednakże, jeśli wykonujesz analizy naukowe używając Pythona, będziesz musiał zainstalować zarówno NumPy jak i SciPy, ponieważ SciPy opiera się na NumPy.
Pakiety w SciPy:
SciPy ma wiele podpakietów dla różnych obliczeń naukowych, które są pokazane w następującej tabeli:

Jednakże, aby uzyskać szczegółowy opis, można zapoznać się z oficjalną dokumentacją.
Pakiety te muszą być importowane wyłącznie przed ich użyciem. Na przykład:
from scipy import cluster
Przed szczegółowym przyjrzeniem się każdej z tych funkcji, spójrzmy najpierw na funkcje, które są wspólne zarówno w NumPy jak i SciPy.
Współdziałanie z NumPy:
SciPy opiera się na NumPy i dlatego można korzystać z funkcji NumPy do obsługi tablic. Aby poznać dogłębnie te funkcje, możesz po prostu skorzystać z funkcji help(), info() lub source().
help():
Aby uzyskać informacje o dowolnej funkcji, możesz skorzystać z funkcji help(). Istnieją dwa sposoby użycia tej funkcji:
- bez parametrów
- z użyciem parametrów
Oto przykład, który pokazuje obie z powyższych metod:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
Gdy wykonasz powyższy kod, pierwsza funkcja help() zwróci informacje o podmodule klastra. Druga help() prosi użytkownika o podanie nazwy dowolnego modułu, słowa kluczowego, itp. Aby zatrzymać wykonywanie tej funkcji, po prostu wpisz 'quit’ i naciśnij enter.
info():
Ta funkcja zwraca informacje o żądanych funkcjach, modułach, itp.
scipy.info(cluster)
source():
Kod źródłowy jest zwracany tylko dla obiektów napisanych w Pythonie. Ta funkcja nie zwraca użytecznych informacji w przypadku, gdy metody lub obiekty są napisane w innym języku, takim jak C. Jeśli jednak chcesz skorzystać z tej funkcji, możesz to zrobić w następujący sposób:
scipy.source(cluster)
Funkcje specjalne:
SciPy udostępnia wiele funkcji specjalnych, które są używane w fizyce matematycznej, takich jak funkcje eliptyczne, funkcje dogodności, gamma, beta itp. Aby wyszukać wszystkie funkcje, możesz skorzystać z funkcji help(), jak opisano wcześniej.
Funkcje wykładnicze i trygonometryczne:
Pakiet funkcji specjalnych programu SciPy dostarcza szereg funkcji, dzięki którym możesz znaleźć wykładniki i rozwiązać problemy trygonometryczne.
Rozważmy następujący przykład:
EXAMPLE:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
OUTPUT:
1000.0
8.0
1.0
0.7071067811865475
Istnieje wiele innych funkcji obecnych w pakiecie funkcji specjalnych SciPy, które możesz wypróbować dla siebie.
Funkcje całkujące:
SciPy dostarcza wiele funkcji do rozwiązywania całek. Począwszy od zwykłego integratora różniczkowego do używania reguł trapezowych do obliczania całek, SciPy jest magazynem funkcji do rozwiązywania wszystkich typów problemów z całkami.
Integracja ogólna:
SiPy dostarcza funkcję o nazwie quad do obliczania całki funkcji, która ma jedną zmienną. Granice mogą być ( ), aby wskazać nieskończone granice. Składnia funkcji quad() jest następująca:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Tutaj funkcja będzie całkowana pomiędzy granicami a i b (może być też nieskończona).
Przykład:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
W powyższym przykładzie, funkcja 'a’ jest obliczana pomiędzy granicami 0, 1. Kiedy ten kod jest wykonywany, zobaczysz następujące wyjście.
OUTPUT:
(3.9086503371292665, 4.3394735994897923e-14)
Funkcja całki podwójnej:
SciPy dostarcza dblquad, która może być używana do obliczania całek podwójnych. Całka podwójna, jak wielu z nas wie, składa się z dwóch zmiennych rzeczywistych. Funkcja dblquad() przyjmuje jako parametr funkcję, która ma być całkowana wraz z 4 innymi zmiennymi, które definiują granice oraz funkcje dy i dx.
PRZYKŁAD:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
OUTPUT:
-1.3333333333333335, 1.4802973661668755e-14)
SciPy zapewnia różne inne funkcje do oceny całek potrójnych, całek n, całek Romberga, itp, które można zbadać dalej w szczegółach. Aby znaleźć wszystkie szczegóły na temat wymaganych funkcji, użyj funkcji pomocy.
Funkcje optymalizacyjne:
Scipy.optimize zapewnia wiele powszechnie używanych algorytmów optymalizacyjnych, które można zobaczyć za pomocą funkcji pomocy.
Składa się on zasadniczo z następujących funkcji:
- Unconstrained and constrained minimization of multivariate scalar functions i.e. minimize (np. BFGS, Newton Conjugate Gradient, Nelder_mead simplex, etc)
- Global optimization routines (eg. differential_evolution, dual_annealing, etc)
- Least-squares minimalizacja i dopasowywanie krzywej (np. least_squares, curve_fit, etc)
- Skalarne minimalizatory funkcji jednoargumentowych i wyszukiwacze korzeni (np. minimize_scalar i root_scalar)
- Rozwiązywacze wielowariantowych układów równań wykorzystujące algorytmy takie jak hybrydowe Powella, Levenberga-Marquardta.
Funkcja Rosenbrooka:
Funkcja Rosenbrooka ( rosen) jest problemem testowym używanym dla gradientowych algorytmów optymalizacyjnych. W SciPy definiuje się ją w następujący sposób:

EXAMPLE:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
OUTPUT: 7371.0399999999945
Nelder-Mead:
Metoda Neldera-Meada jest metodą numeryczną często używaną do znajdowania min/maks funkcji w przestrzeni wielowymiarowej. W poniższym przykładzie metoda minimalizacji jest używana wraz z algorytmem Neldera-Meada.
PRZYKŁAD:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
OUTPUT: array()
Funkcje interpolacji:
W dziedzinie analizy numerycznej interpolacja odnosi się do konstruowania nowych punktów danych w ramach zbioru znanych punktów danych. Biblioteka SciPy składa się z podpakietu o nazwie scipy.interpolate, który składa się z funkcji i klas spline, jednowymiarowych i wielowymiarowych (jedno- i wielowymiarowych) klas interpolacji, itp.
Interpolacja jedno- i wielowymiarowa:
Interpolacja jedno- i wielowymiarowa jest zasadniczo dziedziną dopasowywania krzywych, która znajduje krzywą zapewniającą dokładne dopasowanie do serii dwuwymiarowych punktów danych. SciPy dostarcza funkcję interp1d, która może być wykorzystana do wykonania interpolacji jednoczynnikowej.
EXAMPLE:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
OUTPUT:
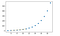
Interpolacja wielozmienna:
Interpolacja wielozmienna (interpolacja przestrzenna) jest rodzajem interpolacji na funkcjach, które składają się z więcej niż jednej zmiennej. Poniższy przykład demonstruje przykład
Interpolacja na siatce 2-D przy użyciu funkcji interp2d(x, y, z) w zasadzie użyje tablic x, y, z do aproksymacji jakiejś funkcji interp2d. f: „z = f(x, y)” i zwraca funkcję, której metoda wywołania używa interpolacji spline do znalezienia wartości nowych punktów.
EXAMPLE:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
OUTPUT:

Fourier Transform Functions:
Analiza Fouriera jest metodą zajmującą się wyrażaniem funkcji jako sumy składowych okresowych i odzyskiwaniem sygnału z tych składowych. Funkcje fft mogą być używane do zwracania dyskretnej transformaty Fouriera rzeczywistej lub złożonej sekwencji.
Przykład:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
Wyjście:
Podobnie, można znaleźć odwrotność tego, używając funkcji ifft w następujący sposób:
EXAMPLE:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
OUTPUT:
Funkcje przetwarzania sygnałów:
Przetwarzanie sygnałów zajmuje się analizą, modyfikacją i syntezą sygnałów, takich jak dźwięk, obrazy itp. SciPy dostarcza pewnych funkcji, za pomocą których można projektować, filtrować i interpolować dane jednowymiarowe i dwuwymiarowe.
Filtrowanie:
Przez filtrowanie sygnału, w zasadzie usuwasz z niego niepożądane komponenty. Aby wykonać uporządkowane filtrowanie, można skorzystać z funkcji order_filter. Funkcja ta w zasadzie wykonuje uporządkowane filtrowanie na tablicy. Składnia tej funkcji jest następująca:
SYNTAX:
order_filter(a, domain, rank)
a = N-wymiarowa tablica wejściowa
domain = tablica masek mająca taką samą liczbę wymiarów jak `a`
rank = Liczba nieujemna, która wybiera elementy z listy po jej posortowaniu (0 jest najmniejsze, a po nim 1…)
Przykład:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
Waveforms:
Pakiet scipy.signal składa się również z różnych funkcji, które mogą być użyte do generowania przebiegów. Jedną z takich funkcji jest chirp. Funkcja ta jest generatorem kosinusów o zmiennej częstotliwości, a jej składnia jest następująca:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)
where,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
OUTPUT:

Algebra liniowa:
Algebra liniowa zajmuje się równaniami liniowymi i ich reprezentacjami za pomocą przestrzeni wektorowych i macierzy. SciPy jest zbudowany na bibliotekach ATLAS LAPACK i BLAS i jest niezwykle szybki w rozwiązywaniu problemów związanych z algebrą liniową. Oprócz wszystkich funkcji z numpy.linalg, scipy.linalg udostępnia również szereg innych zaawansowanych funkcji. Ponadto, jeśli numpy.linalg nie jest używany wraz z obsługą ATLAS LAPACK i BLAS, scipy.linalg jest szybszy niż numpy.linalg.
Finding the Inverse of a Matrix:
Matematycznie, odwrotność macierzy A jest macierzą taką, że gdzie jest macierzą tożsamości składającą się z jedynek na głównej przekątnej oznaczoną jako B=A-1. W SciPy odwrotność tę można uzyskać za pomocą metody linalg.inv.
EXAMPLE:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
OUTPUT:
]
Znajdowanie wyznaczników:
Wartość uzyskana arytmetycznie ze współczynników macierzy jest znana jako wyznacznik macierzy kwadratowej. W SciPy można to zrobić za pomocą funkcji det, która ma następującą składnię:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
where,
a : (M, M) jest macierzą kwadratową
overwrite_a( bool, opcjonalne) : Pozwala na nadpisanie danych w a
check_finite ( bool, opcjonalne): : Sprawdzanie, czy macierz wejściowa składa się tylko z liczb skończonych
EXAMPLE:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
OUTPUT: -5.0
Sparse Eigenvalues:
Wartości własne to specyficzny zestaw skalarów powiązanych z równaniami liniowymi. ARPACK zapewnia, że można znaleźć wartości własne ( wektory własne ) dość szybko. Pełna funkcjonalność ARPACK jest zapakowana w dwa interfejsy wysokiego poziomu, którymi są scipy.sparse.linalg.eigs i scipy.sparse.linalg.eigsh. eigs. Interfejs eigs pozwala znaleźć wartości własne rzeczywistych lub złożonych niesymetrycznych macierzy kwadratowych, podczas gdy interfejs eigsh zawiera interfejsy dla macierzy rzeczywisto-symetrycznych lub kompleksowo-hermitowskich.
Funkcja eigh rozwiązuje uogólniony problem wartości własnych dla złożonej macierzy hermitowskiej lub rzeczywistej macierzy symetrycznej.
EXAMPLE:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
OUTPUT:
Wybrane wartości własne :
Kompleksowa tablica ndarray :
]
Przestrzenne struktury danych i algorytmy:
Dane przestrzenne zasadniczo składają się z obiektów, które są zbudowane z linii, punktów, powierzchni itp. Pakiet scipy.spatial w SciPy może obliczać diagramy Voronoi, triangulacje, itp. przy użyciu biblioteki Qhull. Składa się również z implementacji KDTree dla zapytań o najbliższy punkt sąsiedni.
Triangulacje Delaunay’a:
Matematycznie, triangulacje Delaunay’a dla zbioru dyskretnych punktów na płaszczyźnie jest triangulacją taką, że żaden punkt w danym zbiorze punktów nie znajduje się wewnątrz obwodu dowolnego trójkąta.
Przykład:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
WYJŚCIE:

Wielowymiarowe funkcje przetwarzania obrazów:
Obróbka obrazów zasadniczo zajmuje się wykonywaniem operacji na obrazie w celu odzyskania informacji lub uzyskania ulepszonego obrazu z oryginalnego. Pakiet scipy.ndimage składa się z szeregu funkcji przetwarzania i analizy obrazów zaprojektowanych do pracy z tablicami o dowolnych wymiarach.
Konwolucja i korelacja:
SciPy dostarcza szereg funkcji, które pozwalają na korelację i konwertowanie obrazów.
- Funkcja correlate1d może być użyta do obliczenia jednowymiarowej korelacji wzdłuż danej osi
- Funkcja correlate umożliwia wielowymiarową korelację dowolnej tablicy z określonym jądrem
- Funkcja convolve1d może być użyta do obliczenia jednowymiarowejwymiarową konwolucję wzdłuż danej osi
- Funkcja convolve umożliwia wielowymiarową konwolucję dowolnej tablicy z określonym jądrem
Przykład:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
OUTPUT: array()
Plik IO:
Pakiet scipy.io dostarcza wielu funkcji, które pomagają zarządzać plikami o różnych formatach, takich jak pliki MATLAB, pliki IDL, pliki Matrix Market, itp.
Aby skorzystać z tego pakietu, będziesz musiał zaimportować go w następujący sposób:
import scipy.io as sio
W celu uzyskania pełnych informacji na temat podpakietu, możesz odnieść się do oficjalnego dokumentu na temat File IO.
To prowadzi nas do końca tego SciPy Tutorial. Mam nadzieję, że zrozumiałeś wszystko jasno. Upewnij się, że ćwiczysz tak dużo, jak to możliwe.
Jeśli chcesz sprawdzić więcej artykułów na temat najmodniejszych technologii na rynku, takich jak sztuczna inteligencja, DevOps, Ethical Hacking, to możesz odwołać się do oficjalnej strony Edureka.
Wyglądaj na inne artykuły z tej serii, które wyjaśnią różne inne aspekty Pythona i Data Science.
1. Machine Learning Classifier in Python
2. Python Scikit-Learn Cheat Sheet
3. Machine Learning Tools
4. Python Libraries For Data Science And Machine Learning
5. Chatbot w Pythonie
6. Kolekcje w Pythonie
7. Moduły Pythona
8. Umiejętności programisty Pythona
9. OOPs Pytania i odpowiedzi
10. CV dla programisty Pythona
11. Eksploracyjna analiza danych w Pythonie
12. Snake Game With Python’s Turtle Module
13. Wynagrodzenie programisty Pythona
14. Principal Component Analysis
15. Python kontra C++
16. Scrapy Tutorial
17. Web Scraping With Python
18. Least Squares Regression Method
19. Jupyter Notebook Cheat Sheet
20. Podstawy języka Python
21. Wzorce programowe w Pythonie
22. Generatory w Pythonie
23. Dekorator w Pythonie
24. Python Spyder IDE
25. Aplikacje mobilne z wykorzystaniem Kivy w Pythonie
26. Top 10 Best Books To Learn & Practice Python
27. Robot Framework With Python
28. Gra w węża w Pythonie przy użyciu PyGame
29. Django Interview Questions and Answers
30. 10 najlepszych aplikacji w Pythonie
31. Tablice i haszmapy w Pythonie
32. Python 3.8
33. Wektorowa maszyna wsparcia
34. Samouczek Pythona
.