Każdy elektron w atomie może być jednoznacznie zidentyfikowany przez zestaw czterech liczb kwantowych.

Choć ich odkrycie wymagało zaawansowanej matematyki, wszystkie one są liczbami konwencjonalnymi: trzy z nich mogą przyjmować tylko proste wartości całkowite; czwarta jest ułamkiem zwykłym.
Pierwsze trzy liczby kwantowe wynikają z funkcji falowej, Ψ, otrzymanej przez rozwiązanie równania Schrödingera.
Czwarta liczba kwantowa, spin elektronu, wynika z odkrycia, że elektrony mają dwie możliwe orientacje.
Liczby i ich definicje są następujące:
Liczby kwantowe
| Liczba kwantowa | Nazwa | Możliwe wartości | Informacje | |
|---|---|---|---|---|
| n | pierwotna liczba kwantowa | 1, 2, 3,…., n | określa powłokę energetyczną zajmowaną przez elektron. Powłoki najbliższe jądra mają najniższą wartość n i najniższą energię potencjalną.n jest liczbą pierwszą zapisaną w konfiguracjach elektronowych takich jak magnezu: 1s2 2s2 2p6 3s2 |
|
| l | orbitalny moment pędu liczba kwantowa (zwana też azymutalną liczbą kwantową) |
0, 1, 2,…, (n-1) | …., (n-1) | Definiuje podpowłoki energetyczne – w układach z więcej niż jednym elektronem, podpowłoki mają różne energie. l określa literę podpowłoki w konfiguracjach elektronowych. Na przykład: 1s2 2s2 2p6 3s2 l = 0 daje podpowłokę s. l = 1 daje podpowłokę p. l = 2 daje podpowłokę d, itd. |
| ml | magnetyczna liczba kwantowa | -l, (l+1), …, 0,… , (l+1), l | określa orientację orbitalu podpowłoki. Powłoka p, z l = 1, ma trzy wartości ml: -1, 0, 1.Wskazują one na istnienie trzech orbitali p.tj. orbitali px, py, i pz. Powłoka d, z l = 2, ma pięć wartości ml: -2, -1, 0, 1, 2.Wskazują one na istnienie pięciu orbitali d. |
|
| ms | elektronowa spinowa liczba kwantowa | -½ lub +½ | Elektrony mają dwie możliwe orientacje spinu. |
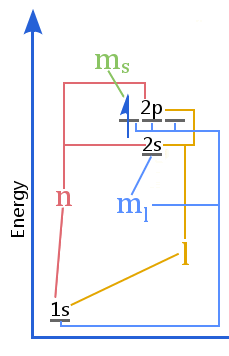
Schemat poziomów energetycznych pokazuje związek pomiędzy liczbami kwantowymi a powłokami, podpowłokami, orbitalami i spinem elektronu w atomie.
Żaden elektron w atomie nie dzieli wszystkich czterech liczb kwantowych.Każdy elektron może być jednoznacznie zidentyfikowany przez jego liczbę kwantową – patrz zasada wykluczenia Pauliego.
Kształty orbitali nie są dane przez liczby kwantowe, ale są gęstościami prawdopodobieństwa – trójwymiarowymi mapami przestrzeni wokół jądra, gdzie elektron znajdzie się w 99 procentach czasu.Kształty orbitali otrzymuje się z kwadratu funkcji falowej, Ψ2.Dokładne położenie i pęd dowolnego elektronu nigdy nie mogą być znane – patrz zasada nieoznaczoności Heisenberga.

.