How To Think With Exponents And Logarithms

Here’s a trick for thinking through problems involving exponents and logs. Wystarczy zadać dwa pytania:

1) Czy mówimy o danych wejściowych (przyczyna zmiany), czy o danych wyjściowych (faktyczna zmiana, która nastąpiła?)

Logarytmy ujawniają dane wejściowe, które spowodowały wzrost
Wykładniki znajdują ostateczny wynik wzrostu

2) Czy mówimy o perspektywie hodowcy, czy obserwatora?

e i logarytm naturalny są z perspektywy moment-by-instant hodowcy
Baza 10, Baza 2, itd. są miary wygodne dla ludzkiego obserwatora

W mojej głowie, I umieścić opcje w tabeli:

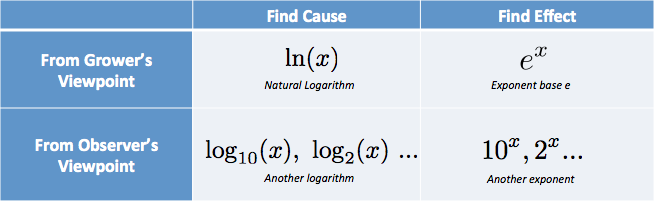
exponent logarithm punkt widzenia porównanie

Mam myśli jak „Potrzebuję przyczyny, z perspektywy hodowcy … to jest naturalny log.”. (Log naturalny jest skracany małymi literami LN, od high-falutin’ logarithmus naturalis.)

Byłem sfrustrowany zajęciami, które opisywały wewnętrzną część tabeli, surowe funkcje, bez podpisów, które wyjaśniały, kiedy ich używać!

To nie poleci, zdobądźmy bezpośrednią praktykę myślenia z logami i wykładnikami.

Scenariusz: Opisywanie wzrostu PKB

Oto typowy przykład wzrostu:

Od 2000 do 2010 roku PKB Stanów Zjednoczonych zmienił się z 9,9 biliona do 14,4 biliona

Ok, jasne, te liczby pokazują, że zmiana nastąpiła. Ale my prawdopodobnie chcemy wglądu w przyczynę: Jaka średnia roczna stopa wzrostu odpowiadałaby tej zmianie?

Od razu mój mózg myśli „logarytmy”, ponieważ pracujemy wstecz od wzrostu do stopy, która go spowodowała. Zaczynam od myśli takiej jak ta:

displaystyle{text{logarytm zmiany} \rightarrow \text{przyczyna wzrostu} Po pierwsze, jakiego logarytmu powinniśmy użyć?

Domyślnie wybieram logarytm naturalny. Większość zdarzeń kończy się w kategoriach rosnącego (nie obserwatora), a ja lubię „jeździć razem” z rosnącym elementem, aby zwizualizować to, co się dzieje. (Radiany są podobne: mierzą kąty w kategoriach poruszyciela.)

Następne pytanie: do jakiej zmiany stosujemy logarytm?

Naprawdę interesuje nas tylko stosunek między początkiem a końcem: 9,9 biliona do 14,4 biliona w ciągu 10 lat. Jest to taka sama stopa wzrostu jak przejście z 9,90 do 14,40 dolarów w tym samym okresie.

Możemy wyostrzyć naszą myśl:

$displaystyle{text{naturalny logarytm współczynnika wzrostu} \rightarrow \text{przyczyna wzrostu} }$

Ok, przyczyną był wskaźnik .374 lub 37,4%. Skończyliśmy?

Jeszcze nie. Logarytmy nie wiedzą, jak długo trwała zmiana (nie włożyliśmy 10 lat, prawda?). Podają nam stopę tak, jakby cała zmiana nastąpiła w jednym okresie czasu.

Zmiana mogła być rzeczywiście jednym rokiem ciągłego wzrostu o 37,4%, lub dwoma latami wzrostu o 18,7%, lub jakąś inną kombinacją.

Z punktu widzenia scenariusza wiemy, że zmiana trwała 10 lat, więc tempo musiało wynosić:

$displaystyle{ \tekst{rate} = \frac{.374}{10} = .0374 = 3.74%}$

Z punktu widzenia natychmiastowego, ciągłego wzrostu, gospodarka USA rosła o 3.74% rocznie.

Czy teraz skończyliśmy? Nie do końca!

Ta ciągła stopa jest z perspektywy hodowcy, tak jakbyśmy „jechali razem” z gospodarką w miarę jej zmian. Bankiera prawdopodobnie obchodzi przyjazna dla człowieka różnica z roku na rok. Możemy się tego dowiedzieć, pozwalając ciągłemu wzrostowi działać przez rok:

$displaystyle{text{exponent with rate and time} \rightarrow \text{efekt wzrostu} }$

$\displaystyle{e^{\text{rate} = ^text{growth}}$

$displaystyle{e^{.0374 ^cdot 1} = 1.0381}$

Roczny przyrost wynosi 3.8%, czyli jest nieco wyższy niż 3.74% natychmiastowej stopy z powodu procentu składanego. Oto inny sposób, aby to ująć:

Przykładowo, dana część gospodarki rośnie o 3,74%, modelowane przez $e^(.0374 * lata)$
Na podstawie rok po roku, z opracowanymi efektami składanymi, gospodarka rośnie o 3,81%, modelowane przez $1,0381^lat$

W finansach, możemy chcieć zmiany w ciągu roku, które można ładnie porównać z innymi trendami. W nauka i inżynieria, my preferować modelowanie zachowanie na natychmiastowy podstawa.

Scenariusz: Opisanie naturalnego wzrostu

Nie znoszę wymyślonych przykładów typu „Załóżmy, że bakteria podwaja się co 24 godziny, znajdź jej wzór wzrostu.”. Czy kolonie bakterii replikują się w czystych ludzkich odstępach czasu i czy czekamy na dokładne podwojenie?

Lepszy scenariusz: „Hej, znalazłem trochę bakterii, poczekałem godzinę i grudka urosła z 2,3 grama do 2,32 grama. Idę teraz na lunch. Wylicz, ile będziemy mieli, gdy wrócę za 3 godziny.”

Zamodelujmy to. Będziemy potrzebowali logarytmu, aby znaleźć tempo wzrostu, a następnie wykładnika, aby przewidzieć ten wzrost na przyszłość. Podobnie jak poprzednio, na początek zachowajmy wszystko w kategoriach logarytmu naturalnego.

Współczynnik wzrostu wynosi:

displaystyle{text{logarytm zmiany} \rightarrow \text{przyczyna wzrostu} ∗

To jest stawka dla jednej godziny, a ogólny model do projekcji na przyszłość będzie

$displaystyle{ ∗współczynnik ze stawką i czasem} \rightarrow \text{efekt wzrostu} }$

$displaystyle{e^{.0086 \u00} \rightarrow \text{efekt wzrostu} }$

Jeśli zaczniemy od 2,32 i będziemy rosnąć przez 3 godziny, to będziemy mieć:

$displaystyle{2,32 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^{.0086 ^}} = 2,38}$

Tak dla zabawy, jak długo potrwa, zanim bakteria się podwoi? Wyobraźmy sobie, że czekamy, aż 1 zamieni się w 2:

$displaystyle{1 ^{.0086 ^{hours}} = 2}$

Możemy mechanicznie wziąć log naturalny z obu stron, aby „cofnąć wykładnik”, ale pomyślmy intuicyjnie.

Jeśli 2 jest wynikiem końcowym, to ln(2) jest wkładem wzrostu, który nas tam doprowadził (jakieś tempo × czas). Wiemy, że tempo wynosiło .0086, więc czas dojścia do 2 wyniesie:

$displaystyle{ \text{hours} = \frac{ln(2)}{ \text{rate} = \frac{.693}{.0086} = 80.58}$

Kolonia podwoi się po ~80 godzinach. (Dobrze, że nie zostałeś w pobliżu?)

Co naprawdę oznacza zmiana perspektywy?

Ustalenie, czy chcesz dane wejściowe (przyczyna wzrostu) czy wyjściowe (wynik wzrostu) jest całkiem proste. Ale jak zwizualizować perspektywę hodowcy?

Wyobraźmy sobie, że mamy małych robotników, którzy budują ostateczny wzór wzrostu (patrz artykuł o wykładnikach):

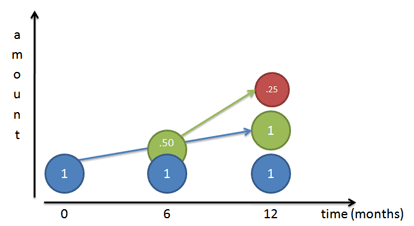
$odsetek składany$

Jeśli nasza stopa wzrostu wynosi 100%, to mówimy naszemu początkowemu robotnikowi (Panu Niebieskiemu), aby pracował wytrwale i stworzył 100% kopii samego siebie do końca roku. Jeśli podążamy za nim dzień po dniu, widzimy, że kończy 100% kopię siebie (Pan Zielony) na koniec roku.

Ale… ten robotnik, którego budował (Pan Zielony) również zaczyna pracować. Jeśli Pan Zielony po raz pierwszy pojawia się na 6-miesięcznym znaku, ma pół roku do pracy (ten sam roczny wskaźnik co Pan Niebieski) i buduje Pana Czerwonego. Oczywiście, Pan Czerwony kończy się być w połowie zrobione, ponieważ Pan Zielony ma tylko 6 miesięcy.

Co by było, gdyby Pan Zielony pojawił się po 4 miesiącach? Miesiąc? Dzień? Sekundę? Jeśli pracownicy zaczną rosnąć natychmiast, otrzymamy krzywą instant-by-instant określoną przez $e^x$:

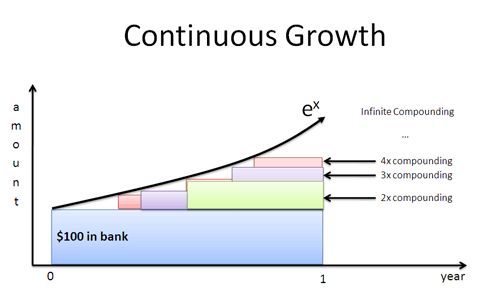
wzrost ciągły

Log naturalny daje stopę wzrostu w kategoriach perspektywy pojedynczego pracownika. Wstawiamy tę stopę do $e^x$, aby znaleźć ostateczny wynik, z uwzględnieniem wszystkich składanych wartości.

Używanie innych podstaw

Przełączenie się na inny rodzaj logarytmu (podstawa 10, podstawa 2, itd.) oznacza, że szukamy jakiegoś wzorca w ogólnym wzroście, a nie tego, co robi indywidualny pracownik.

Każdy logarytm zadaje pytanie, gdy widzimy zmianę:

Log podstawy e: Jakie było chwilowe tempo pracy każdego robotnika?
Log base 2: Ile podwojeń było potrzebnych?
Log base 10: Ile podwojeń 10x było potrzebnych?

Oto scenariusz do przeanalizowania:

W ciągu 30 lat liczba tranzystorów w typowych układach scalonych wzrosła z 1000 do 1 miliarda

Jak byś to przeanalizował?

Mikrochipy nie są jedną całością, która płynnie rośnie w czasie. Są to oddzielne edycje, z konkurencyjnych firm, i wskazują na ogólny trend technologiczny.
Ponieważ nie „jedziemy razem” z rozwijającym się mikroprocesorem, użyjmy skali stworzonej dla ludzkiej wygody. Łatwiej jest myśleć o podwojeniu niż o 10-krotnym zwiększeniu.

Przy tych założeniach otrzymujemy:

displaystyle{text{logarytm zmiany} \rightarrow \text{przyczyna wzrostu} }

$displaystyle{log_2(\frac{tekst{1 mld}}{1000}) = \log_2(\tekst{1 mln}) \sim \tekst{20 podwojeń}}$

„Przyczyną wzrostu” było 20 podwojeń, o których wiemy, że nastąpiły w ciągu 30 lat. To średnio 2/3 podwojenia na rok, lub 1,5 roku na podwojenie – miła zasada kciuka.

Z perspektywy hodowcy, obliczylibyśmy $ln(\tekst{1 miliard}/1000) / \tekst{30 lat} = 46%$ ciągłego wzrostu (trochę trudniej odnieść się do tego scenariusza).

Możemy podsumować naszą analizę w tabeli:

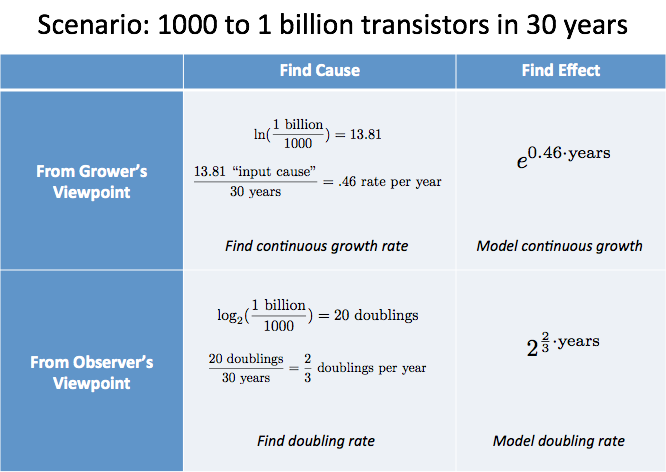
exponents transistor example

Summary

Uczenie się polega na znajdowaniu ukrytych napisów kryjących się za daną koncepcją. Kiedy jest ono używane? Jaki punkt widzenia wnosi do problemu?

Moja obecna interpretacja jest taka, że wykładniki pytają o przyczynę i skutek oraz hodowcę i obserwatora. Ale nigdy nie skończyliśmy; częścią zabawy jest obserwowanie, jak możemy przypomnieć sobie stare koncepcje.

Wesołej matematyki.

Załącznik: The Change Of Base Formula

Oto jak myśleć o zmianie baz. Zakładając 100% ciągłe tempo wzrostu,

ln(x) to czas wzrostu do x
ln(2) to czas wzrostu do 2

Ponieważ mamy czas na podwojenie, możemy zobaczyć, ile „zmieściłoby się” w całkowitym czasie wzrostu do x:

$displaystyle{text{liczba podwojeń od 1 do x} = ∗frac{ln(x)} = ∗log_2(x)}$

Na przykład, ile podwojeń występuje od 1 do 64?

Cóż, ln(64) = 4,158. A ln(2) = .693. Liczba podwojeń, które pasują, to:

W realnym świecie kalkulatory mogą tracić precyzję, więc jeśli to możliwe, używaj bezpośredniej funkcji log base 2. I oczywiście, możemy mieć liczbę ułamkową: Uzyskanie od 1 do pierwiastka kwadratowego z 2 jest „połową” podwojenia, lub log2(1,414) = 0,5.

Zamiana na logarytm bazowy 10 oznacza, że liczymy liczbę 10-krotności, które pasują:

$<displaystyle{text{liczba 10-krotności od 1 do x} = \frac{ln(x)}{ln(10)} = \log_{10}(x) }$

Niezłe, prawda? Przeczytaj Using Logarithms in the Real World, aby uzyskać więcej przykładów.

Inne posty z tej serii

An Intuitive Guide To Exponential Functions & e
Demystifying the Natural Logarithm (ln)
A Visual Guide to Simple, Compound and Continuous Interest Rates
Common Definitions of e (Colorized)
Understanding Exponents (Why does 0^0 = 1?)
Używanie logarytmów w prawdziwym świecie
Jak myśleć za pomocą wykładników i logarytmów
Zrozumienie dyskretnego i ciągłego wzrostu
Co naprawdę oznacza wykładnik?
Pytanie: Dlaczego e jest szczególne? (2,718…, a nie 2, 3,7 lub inna liczba?)