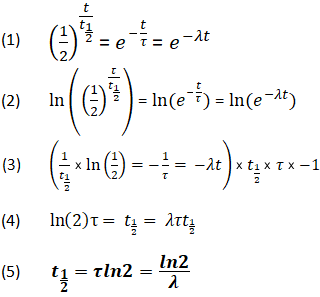Następujące narzędzia mogą wygenerować dowolną z wartości z pozostałych trzech we wzorze na czas połowicznego rozpadu substancji zmniejszający się o połowę.

Kalkulator czasu połowicznego rozpadu
Podaj dowolne trzy z poniższych, aby obliczyć czwartą wartość.
Półokres życia, średni czas życia i konwersja stałej rozpadu
Proszę podać dowolną z poniższych informacji, aby uzyskać dwie pozostałe wartości.
Definicja i wzór
Półokres życia definiuje się jako ilość czasu, jaką zajmuje danej wielkości zmniejszenie się do połowy jej wartości początkowej. Termin ten jest najczęściej używany w odniesieniu do atomów ulegających rozpadowi promieniotwórczemu, ale może być stosowany do opisu innych rodzajów rozpadu, wykładniczego lub nie. Jednym z najbardziej znanych zastosowań czasu połowicznego rozpadu jest datowanie węglem-14. Okres połowicznego zaniku węgla-14 wynosi około 5 730 lat i może być wiarygodnie wykorzystany do pomiaru dat do około 50 000 lat temu. Proces datowania węglem-14 został opracowany przez Williama Libby’ego i opiera się na fakcie, że węgiel-14 jest stale produkowany w atmosferze. Jest on wbudowywany w rośliny w procesie fotosyntezy, a następnie w zwierzęta, gdy spożywają one rośliny. Węgiel-14 ulega rozpadowi radioaktywnemu po śmierci rośliny lub zwierzęcia, a pomiar ilości węgla-14 w próbce dostarcza informacji o tym, kiedy roślina lub zwierzę zmarło.
Poniżej przedstawiono trzy równoważne wzory opisujące rozkład wykładniczy:
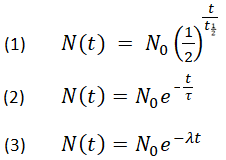
- gdzie
N0 jest ilością początkową
Nt jest ilością pozostałą po czasie, t
t1/2 jest okresem połowicznego rozpadu
τ jest średnim czasem życia
λ jest stałą rozpadu
Jeśli archeolog znalazł próbkę kopalną, która zawierała 25% węgla-14 w porównaniu z próbką żywą, czas śmierci próbki kopalnej mógłby być określony przez przekształcenie równania 1, ponieważ Nt, N0, i t1/2 są znane.
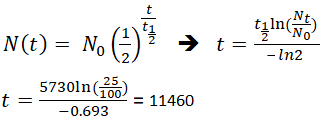
To oznacza, że skamielina ma 11 460 lat.
Odwzorowanie związku między stałymi połówkowymi
Używając powyższych równań, możliwe jest również wyprowadzenie związku między t1/2, τ i λ. Związek ten umożliwia wyznaczenie wszystkich wartości, o ile przynajmniej jedna z nich jest znana.