Kinematyka rotacyjna - Fizyka 298

„Ludzie mówią o zabijaniu czasu, podczas gdy czas po cichu ich zabija”
Dion Boucicault – London Assurance (1841)

Do tej pory rozważaliśmy kinematykę i dynamikę cząstek, w tym ruch translacyjny i kołowy, a także ruch translacyjny układów cząstek (w szczególności ciał sztywnych) w kategoriach ruchu środka masy układu (ciała). W tym ostatnim przypadku możemy sobie wyobrazić, że cała masa obiektu znajduje się w środku masy, jeśli chodzi o zewnętrzne siły translacyjne.

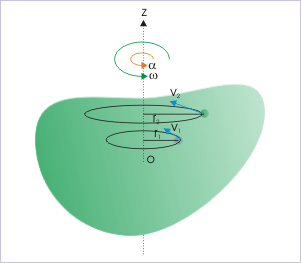Kolejnym krokiem jest rozważenie obrotu ciała sztywnego wokół ustalonej osi obrotu. Zauważmy, że ponieważ rozpatrujemy ciało sztywne, to każda cząstka w tym ciele pozostaje nieruchoma względem pozostałych. Oznacza to, że w takim ruchu obrotowym każda cząstka porusza się po okręgu, którego środek leży na osi obrotu. Na rysunku po prawej stronie obiekt obraca się wokół osi z, a dwie przykładowe cząstki poruszają się po okręgach o promieniach r1 i r2. Jeśli potrafimy opisać ruch kołowy cząstki bez bezpośredniego odniesienia do jej promienia, to wszystkie cząstki w układzie będą opisane tym samym układem równań. Mimo, że promienie cząstek są różne, ich obroty kątowe są identyczne. Dlatego konieczne jest wprowadzenie zmiennych kątowych.

Miara radianowa kątów

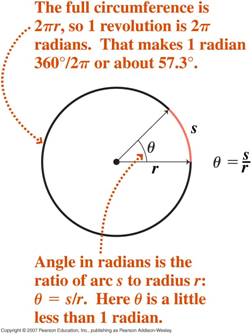
Prędkość kątowa i przyspieszenie kątowe

Prędkość kątowa i przyspieszenie kątowe są zdefiniowane w podobny sposób jak prędkość i przyspieszenie. Istnieją wartości średnie i chwilowe każdego z nich.

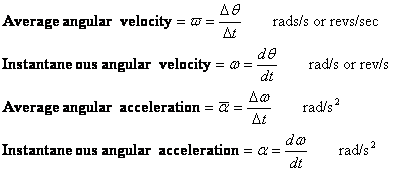
Przyspieszenie kątowe nie jest tym samym co przyspieszenie dośrodkowe. Przyspieszenie dośrodkowe wynika ze zmiany kierunku prędkości, przyspieszenie kątowe wynika ze zmiany wielkości prędkości (przez kąt obrotu).

Dokładnie tak samo jak w przypadku translacji, różnica między prędkością kątową a prędkością kątową polega na kierunku. Prędkość kątowa musi zawierać kierunek obrotu wokół danej osi. Na przykład, 10 rad/s zgodnie z ruchem wskazówek zegara wokół osi x jest prędkością kątową, 10 rad/s wokół osi x jest prędkością kątową.

Rotacyjne równania kinematyczne

Przez bezpośrednią analogię do translacyjnych równań kinematycznych, ruch po okręgu wokół jednej osi przy stałym przyspieszeniu kątowym może być opisany następującymi czterema równaniami,

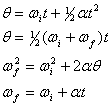
gdzie dokonaliśmy podstawienia,

Zauważmy, że tak jak +x jest zdefiniowane arbitralnie w prawo, tak dodatnia wartość theta może być zdefiniowana jako zgodna lub przeciwna do ruchu wskazówek zegara.

Zależność między zmiennymi kątowymi i translacyjnymi

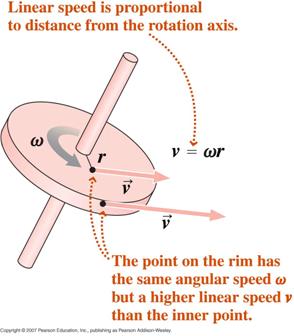Wychodząc od definicji miary radianowej, przez różniczkowanie względem czasu, możemy pokazać, że,

gdzie v jest prędkością styczną, a a jest przyspieszeniem stycznym.

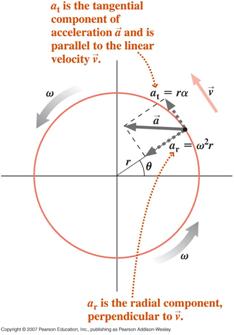
Cząstka wykonująca ruch okrężny, ze zmienną prędkością kątową (ruch okrężny niejednostajny), doświadczy dwóch składowych przyspieszenia, składowej stycznej ze względu na zmieniającą się wielkość jej prędkości i składowej radialnej (dośrodkowej) ze względu na zmieniający się kierunek jej prędkości

Przyspieszenie netto cząstki jest sumą wektorową tych dwóch składowych, jak wskazano poniżej.

Dla twojej informacji…

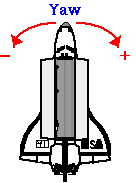
Jednoczesny obrót wokół więcej niż jednej osi może być rozważany w podobny sposób jak ruch pocisku, gdzie rozszerzyliśmy naszą dyskusję o translacji 1D na ruch 2D. W zastosowaniach lotniczych obroty wokół trzech osi są opisywane jako Roll, Pitch i Yaw.