Proporcjonalne jest tylko jednym ze sposobów reagowania na błąd w systemie. Problem ze sterowaniem proporcjonalnym polega na tym, że nie potrafi ono wykrywać trendów i dostosowywać się do nich. Tym zajmuje się sterowanie całkowe.
Po lewej stronie rysunku 6 znajduje się inny przykładowy wykres błędu w systemie w czasie. Ponownie, może to być odległość robota od obiektu, może to być poziom płynu w zbiorniku, lub temperatura w piecu fabrycznym. Być może cel, za którym podąża robot, oddala się od niego z prędkością, której robot nie jest w stanie dogonić. Może uszczelka drzwi pieca jest zużyta; może pobór płynu ze zbiornika jest wyjątkowo duży. Niezależnie od przyczyny, ponieważ sterowanie proporcjonalne nie jest zaprojektowane do reagowania na trendy, nie może wykryć i skorygować problemu. W tym miejscu do akcji wkracza sterowanie integralne.
Integralne mierzy obszar pomiędzy wartościami błędu a osią czasu. Jeśli błąd nie wraca do zera, obszar błędu staje się coraz większy. Prawa strona rysunku 6 pokazuje, jak wyjście całki może reagować na tego rodzaju trend. Wraz ze wzrostem obszaru pomiędzy krzywą błędu a osią czasu, wyjście rośnie proporcjonalnie do tego obszaru. W rezultacie wyjście to napędza siłownik coraz mocniej, aby skorygować błąd.
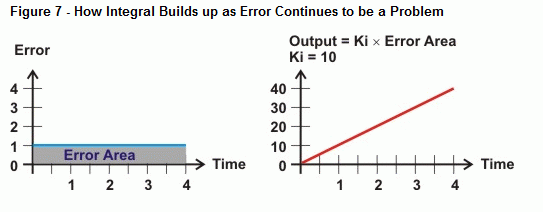
Co się dzieje, gdy błąd nie jest linią prostą, jak krzywa pokazana na rysunku 8? To właśnie określa operacja rachunkowa całkowania, czyli obszar pomiędzy krzywą a osią. W przypadku sterowania całkującego, w miarę upływu czasu z błędem, obszar pod krzywą rośnie, a wraz z nim wartość, którą obliczenia całkowe wykorzystają do przeciwdziałania błędowi systemu. Jeśli krzywa błędu spada poniżej osi czasu, nagromadzenie obszaru ujemnego odejmuje od nagromadzenia obszaru dodatniego. Przy prawidłowym dostrojeniu sterowanie całkowe może pomóc systemowi w osiągnięciu błędu równego zero.
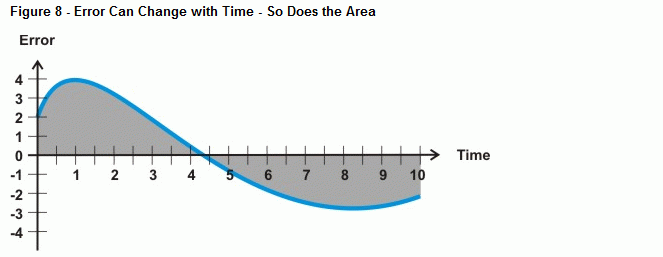
Stempel BASIC może przybliżać błąd pod krzywą za pomocą całkowania numerycznego. Rysunek 9 pokazuje, jak można w przybliżeniu określić błąd pod krzywą przez zsumowanie powierzchni kilku małych prostokątów między krzywą błędu a osią czasu. Obszar każdego pola to błąd pomnożony przez czas pomiędzy pomiarami. Sumując wszystkie obszary pudełek, otrzymujemy przybliżenie obszaru pod krzywą.
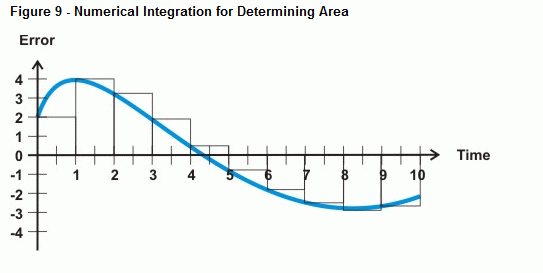
Tak długo, jak twoje pomiary są równomiernie rozmieszczone, możesz nazwać szerokość każdego pudełka wartością 1. To sprawia, że matematyka jest znacznie prostsza niż próba uwzględnienia 20 ms między próbkami, 5 minut między próbkami lub cokolwiek, co okaże się twoją częstotliwością próbkowania. Zamiast mnożyć błąd przez przyrost czasu między próbkami, a następnie dodawać do następnego błędu pomnożonego przez czas, możesz po prostu pomnożyć każdą próbkę błędu przez czas 1. W rezultacie możesz po prostu zachować bieżącą sumę pomiarów błędów do obliczeń całkowych. Oto przykład jak to zrobić za pomocą PBASIC’a:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
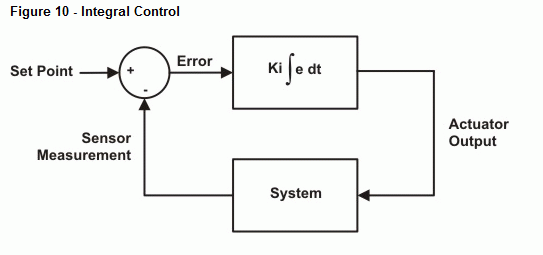
Następny przykładowy program wykonuje całkowanie numeryczne na sygnale błędu i odpowiednio dostosowuje wyjście. Podobnie jak w przypadku sterowania proporcjonalnego, istnieje stała, która skaluje wyjście całkowania do pożądanej wartości. Dla uproszczenia ponownie użyjemy wartości 10 dla Ki. Rysunek 10 przedstawia schemat blokowy pętli sterowania. Określenie Kp ∫ edt odnosi się do Kp pomnożonego przez całkę błędu w czasie. Innymi słowy, Kp pomnożone przez skumulowany obszar między krzywą błędu a osią czasu.
Przykładowy program – IntegralAlgorithm.bs2
- Wprowadź, zapisz i uruchom IntegralAlgorithm.bs2.
- Wprowadź tę sekwencję wartości do okienka transmisji Debug Terminala: 3 3 3 3 3 3 3 3 3. Zauważ, jak wyjście całki staje się większe za każdym razem, gdy powtarza się 3. To jest praca całki, aby wykryć trendy i zwiększyć napęd, aby skorygować go w razie potrzeby.
- Teraz spróbuj tej sekwencji: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. Obszar pod tą krzywą wynosi 0, ponieważ obszar ujemny jest taki sam jak obszar dodatni. To jest również to, do czego dojdzie obliczenie całkowe, gdy skończysz wprowadzać sekwencję.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
How IntegralAlgorithm.bs2 Works
Ten program jest ProportionalAlgorithm.bs2 zmodyfikowanym tak, aby zamiast tego wykonywał obliczenia całkowe. Istnieją teraz dwa różne rodzaje błędów do śledzenia, więc tablica zmiennych błędu została rozszerzona do dwóch elementów. Zmienna error(0) śledzi błąd bieżący, a error(1) – błąd skumulowany. Stałe Current CON 0 i Accumulator CON 1 sprawiają, że księgowanie jest trochę bardziej sensowne, z error(current) i error(accumulator).
Inną zmianą, która została dokonana jest to, że błąd jest akumulowany i wyjście całkowe jest obliczane za pomocą tych dwóch stwierdzeń:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Your Turn – Clamping the Integral Output
Jak mogłeś się zorientować po wielokrotnym wpisywaniu 3 do Debug Terminala, wyjście całkowe napędu może naprawdę zacząć uciekać. Możesz użyć operatorów MIN i MAX, aby nie dopuścić do tego, aby integralne sterowanie przesadziło z wyjściem. Powtórzmy działanie z offsetem serwonapędu i ograniczmy wyjście od 650 do 850.
- Zmień instrukcję drive = i na drive = i + Offset MIN 650 MAX 850.
- Uruchom program i sprawdź, czy wyjście całki jest ograniczone do wartości pomiędzy 650 a 850. Spróbuj wprowadzić 2 wielokrotnie, a następnie -2 wielokrotnie.
.