
Sieci neuronowe i matematyka są nierozłączne i to chyba właśnie przeraża większość ludzi. Słyszałem zbyt wiele wątpliwych uwag na temat Deep Learning, „Och to jest zbyt dużo matematyki dla mnie, aby pojąć”, „Ile firm używa Deep Learning naprawdę? Wolałbym oszczędzić sobie łamania mózgu i trzymać się z dala od tych wymagających koncepcji”.
Ale jeśli się nad tym zastanowić, to nie jest to takie trudne. Zaufaj mi! Aby zrozumieć, dlaczego algorytm zachowuje się w określony sposób, konieczne jest zrozumienie, co dzieje się za kulisami. Złożone algorytmy uczenia maszynowego są dziś dla nas wygodnie zapakowane i wystarczy tylko wywołać funkcję. Pochodne funkcji aktywacji są nieco mniej oczywistymi pojęciami, które często ignorujemy. Stanowią one jednak podstawę potężnych algorytmów i włożenie odrobiny dodatkowego wysiłku, aby je zrozumieć, z pewnością się opłaci. Po przeczytaniu tego artykułu będziesz o krok bliżej do rozszyfrowania tego, co kryje się pod fasadą „czarnej skrzynki”.
Tło
Sieci neuronowe wykorzystują różne funkcje aktywacji w warstwach ukrytych i wyjściowych, aby katalizować proces uczenia się. Kilka powszechnie stosowanych funkcji aktywacji obejmują Sigmoid i tanH funkcji. Najbardziej popularną funkcją aktywacji jest ReLU (Rectified Linear Unit) ze względu na jej zdolność do skutecznego przezwyciężenia problemu znikającego gradientu. Dogłębny wgląd w funkcje aktywacji jest na inny dzień. Dziś skupimy się na matematyce stojącej za pochodną funkcji Sigmoid.
Dlaczego pochodna funkcji aktywacji jest ważna?
Jak zapewne wiesz, dwa kroki napędzają sieci neuronowe:
- Prognozowanie w przód – Dane wejściowe przepływają przez sieć i otrzymujemy przewidywane wyjście. Porównujemy go z rzeczywistym wyjściem i obliczamy error.
- Back Propagation – Obliczony błąd jest używany do aktualizacji parametrów sieci neuronowej przy użyciu pochodnej funkcji aktywacji.
Funkcja sigmoidalna
Funkcja sigmoidalna, charakteryzująca się krzywą w kształcie litery S, jest często określana jako specjalny przypadek funkcji logistycznej. Jest ona najbardziej przydatna w przypadkach, gdy musimy przewidzieć prawdopodobieństwo jako wartość wyjściową.
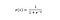
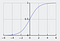
Funkcja sigmoidalna wyprowadza wartości, które leżą pomiędzy 0 a 1 (słusznie, biorąc pod uwagę, że przewiduje prawdopodobieństwa).
Pochodna sigmoidalna
Ten fundamentalny blok konstrukcyjny, który pomaga trenować sieci neuronowe, przyjmuje postać:


Bez dalszych ceregieli, zajmijmy się pochodną!
Podejście 1

Podejście 2:
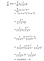
Dlaczego używamy tej wersji pochodnej?
W kroku propagacji w przód, obliczamy funkcję sigmoidalną (σ(x)) i mamy jej wartość pod ręką. Podczas obliczania pochodnej w kroku propagacji wstecznej, wszystko co musisz zrobić to wstawić wartość σ(x) do wzoru wyprowadzonego powyżej i voila, możesz zaczynać!
To jest to, chłopaki! Dzięki za przeczytanie!