Wprowadzenie
Przekształcenia współrzędnych są wystarczająco nieintuicyjne w 2-D, i bardzo bolesne w 3-D. Na tej stronie zajmiemy się nimi w następującej kolejności: (i) wektory w 2-D, (ii) tensory w 2-D, (iii) wektory w 3-D, (iv) tensory w 3-D, i wreszcie (v) przekształcenia tensorowe 4 rangi.
Głównym aspektem przekształceń współrzędnych jest ocena macierzy przekształcenia, szczególnie w 3-D. Jest to poruszone tutaj i omówione szczegółowo na następnej stronie.
Jest bardzo ważne, aby rozpoznać, że wszystkie przekształcenia współrzędnych na tej stronie są rotacją układu współrzędnych, podczas gdy sam obiekt pozostaje nieruchomy. Obiektem” może być wektor, taki jak siła lub prędkość, lub tensor, taki jak naprężenie lub odkształcenie w elemencie. Obroty obiektów są omówione w późniejszych rozdziałach.
2-D Transformacje współrzędnych wektorów
Akademicki ziemniak stanowi doskonały przykład zastosowania transformacji współrzędnych do wektorów, podkreślając jednocześnie, że to układ współrzędnych się obraca, a nie wektor… lub ziemniak.
Ziemniak po lewej stronie ma na sobie wektor. Ale bez układu współrzędnych nie ma sposobu na opisanie tego wektora. Do ziemniaka dodano więc układ współrzędnych, jak na rysunku po prawej, dzięki czemu wektor można teraz opisać jako \(\bf v} = 2{\bf i} + 9{\bf j}\).

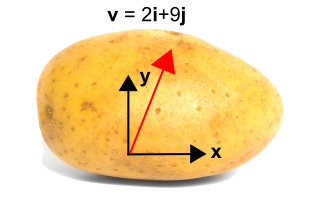
Więc teraz wprowadzamy obrócony układ współrzędnych pokazany na niebiesko poniżej, używając x’™ i y’™. Nowy układ jest obracany przeciwnie do ruchu wskazówek zegara o kąt Δt od początkowego układu współrzędnych. Zauważmy, że sam wektor nie ulega żadnej zmianie. Jest to wciąż ten sam wektor, co poprzednio. Jest on jednak opisany innymi wartościami liczbowymi w nowym układzie współrzędnych. W tym przypadku wektor jest bardziej równoległy do nowej osi x’a niż do osi y’a, więc jego składowa będzie większa niż składowa j’a. Transformacja jest podana pod rysunkiem.
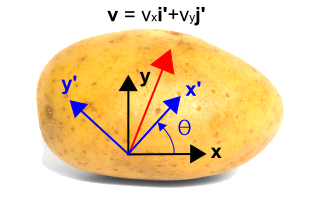
Można to zauważyć zauważając, żeTe cztery czynniki tworzą cztery warunki w równaniach transformacji. Można je łatwo sprawdzić, ustawiając ^theta = 0 ^circ ^) i ^theta = 90 ^circ ^). Gdy \teta = 0 \, wtedy \(v’_x = v_x \) i \(v’_y = v_y \). Gdy \theta = 90^circ\), wtedy \(v’_x = v_y\) i \(v’_y = -v_x\).
Warunki \(\cos \theta\) są na przekątnej macierzy, podczas gdy warunki \(\sin \theta\) są poza przekątną. Jedyną potencjalną trudnością jest zapamiętanie, który z członów \(\sin \theta\) ma znak minus. Zawsze jest to dolny lewy człon.
Powyższe równanie zapisujemy w notacji macierzowej jako
, gdzie Δ(Δbf Q) jest zwykłą literą wybraną dla macierzy przekształcenia.

Macierze przekształcenia a macierze obrotu
Jeśli ten temat nie był już wystarczająco trudny, wiele książek i stron internetowych wprowadza zamieszanie, nie wyjaśniając, co jest stałe, a co obrotowe. Na tej stronie i na następnej, to układ współrzędnych obraca się, podczas gdy obiekt pozostaje nieruchomy, więc termin macierz transformacji jest używany tutaj, aby to podkreślić.
Jednakże później zajmiemy się sytuacjami, w których obiekt obraca się, podczas gdy układ współrzędnych pozostaje nieruchomy. W tym scenariuszu, termin macierz rotacji będzie używany dla podkreślenia, że obiekt się obraca.
Wiele zamieszania wynika z zadziwiającego faktu, że każda macierz (transformacji i rotacji) jest po prostu transpozycją drugiej! Tak więc wyglądają one niezwykle podobnie. W problemach dwuwymiarowych jedyną praktyczną różnicą jest to, czy znak minus przed ὄ (ὄsin ὄta) znajduje się przy członie ὄ (q_{12}}), czy przy członie ὄ (q_{21}}).
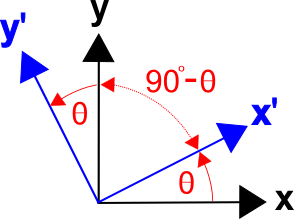
Istnieje ogólna metoda formułowania macierzy przekształceń oparta na cosinusach kątów między osiami dwóch układów współrzędnych, tzn. cosinusach kierunku. (Dotyczy to również przekształceń trójwymiarowych.)Macierz przekształcenia można zapisać jako
gdzie \((x’,x)\) oznacza kąt między osiami \(x’\) i \(x’\),\((x’,y)\) jest kątem między osiami \(x’\) i \(y’\), itd.
Kąt między osiami \(x’\) i \(y’\) wynosi \((90^circ – \theta)\), a \(\cos(x’,y) = \cos(90^circ – \theta) = \sin \theta\).
Podobnie, kąt między \(y’\) i \(x’\) jest \((90^circ + \theta)\), i \(\cos(y’,x) = \cos(90^circ + \theta) = – \sin \theta\).
Notacja tensorowa
Transformację współrzędnych zapisuje się w notacji tensorowej jako
, gdzie \u2002 \u2002 \u2002 \u2002 \u2002 \u2002 \u2002 \u2002 \u2002 (Nie wiem, dlaczego w notacji macierzowej używa się macierzy, ale w notacji tensorowej używa się macierzy (lambda_{ij}}), a nie macierzy (q_{ij}})). \Na przykład, jeśli \(i = 1\) i \(j = 2\), to
\(\lambda_{ij}} jest cosinusem kierunku kąta między osią \(x’_i\) i osią \(x_j). Ponownie, ma to również zastosowanie do przekształceń trójwymiarowych.
2-D Współrzędnościowe przekształcenia tensorów
W tym rozdziale przedstawimy co i jak przekształceń tensorów. Dlaczego trzeba będzie poczekać na później.
Współrzędnościowe przekształcenia tensorów drugiego rzędu angażują tę samą macierz co przekształcenia wektorowe. Przekształcenie tensora naprężeń z referencyjnego układu współrzędnych x-y na tensor w nowym układzie x-y wykonuje się następująco.
Wypisanie macierzy wprost daje
= ∗ lewa strona ∗ lewa strona ∗
(Zauważ, że tensor naprężeń jest zawsze symetryczny, nawet po przekształceniach.Te trzy równania są dokładnie dwuwymiarową transformacją tensora naprężeń wynikającą z sumowania sił na elemencie różniczkowym i narzucenia równowagi. Jest to również reprezentowane przez koło Mohra.
Notacja tensorowa
Transformacja współrzędnych jest zapisana w notacji tensorowej jako
Jak zwykle, notacja tensorowa zapewnia dodatkowy wgląd w proces. Tym razem, wgląd pochodzi z indeksów na lambdach. Każda lambda efektywnie łączy w pary indeks na \(\boldsymbol{sigma’}) z jednym na \(\boldsymbol{sigma}). Jest to prawdą niezależnie od rangi tensora.
Trójwymiarowe przekształcenia współrzędnych wektorów
Wiele ogólnych równań używanych w przekształceniach dwuwymiarowych ma również zastosowanie w trójwymiarowych.Przykłady obejmują
Tylko teraz szczegóły są inne. Wektory mają składowe z, a macierze przekształceń są 3×3, a nie 2×2. Wypróbuj ją.
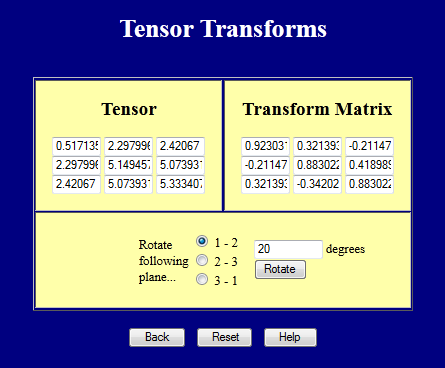
Transformacje współrzędnościowe tensorów czwartego rzędu
W rozdziale o prawie Hooke’a zobaczymy, że tensor sztywności jest czwartego rzędu, tzn. 3x3x3x3 (nie 4×4). Zapisuje się go jako \(C_{ijkl}}), ponieważ odnosi on każdą składową odkształcenia, \(\epsilon_{kl}}, do każdej składowej naprężenia, \(\sigma_{ij}}, tzn, \Prawo transformacji współrzędnych dla tensora sztywności czwartego rzędu można łatwo zapisać w notacji tensorowej jako
Równanie tensorowe podpowiada, jak zapisać transformację w notacji macierzowej.
Podsumowanie
Transformacja współrzędnych wektora w notacji macierzowej i tensorowej to
Transformacja współrzędnych tensora w notacji macierzowej i tensorowej to
Zauważmy, że ∗ (∗ Q}) i ∗ (∗ lambda_{ij}) są tą samą macierzą transformacji.
.