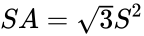Dziennik naukowy, zobacz Tetrahedron (czasopismo).
| Czworościan foremny | |
|---|---|
 (Kliknij tutaj, aby zobaczyć model obrotowy) |
|
| Typ | Ciało stałe platońskie |
| Elementy | F = 4, E = 6 V = 4 (χ = 2) |
| Powierzchnie boków | 4{3} |
| Symbol Schläfli | {3,3} i s{2,2} |
| Symbol Wythoffa | 3 | 2 3 | 2 2 |
| Pierścień Coxetera-Dynkina | |
| Symetria | Td lub (*332) |
| U01, C15, W1 | |
| Właściwości | Deltaedr wypukły regularny |
| Kąt dwuścienny | 70.528779° = arccos(1/3) |
 3.3.3 (figura wierzchołkowa) |
 Self-dual (dualny wielościan) |
 Net |
|
Czworościan foremny (liczba mnoga: tetrahedry) to wielościan złożony z czterech trójkątnych ścian, z których trzy spotykają się w każdym wierzchołku. Czworościan foremny to taki, w którym cztery trójkąty są regularne, czyli „równoboczne”, i jest jedną z brył platońskich.
Czworościan jest jednym z rodzajów ostrosłupa, który jest wielościanem o podstawie wielokąta płaskiego i trójkątnych ścianach łączących podstawę z punktem wspólnym. W przypadku czworościanu podstawą jest trójkąt (każda z czterech ścian może być uważana za podstawę), więc czworościan jest również znany jako ostrosłup trójkątny lub deltościan foremny.
Formuły na czworościan foremny
Objętość wynosi
Powierzchnia wynosi
Template:Commonscat
- F. M. Jackson i Weisstein, Eric W., „Tetrahedron” z MathWorld.
- Weisstein, Eric W., „Tetrahedron” from MathWorld.
- Weisstein, Eric W., „Tetrahedron” from MathWorld.
- Wielościan jednolity
- Tetrahedron: Interactive Polyhedron Model
- K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Piero della Francesca’s formula for tetrahedron volume at MathPages
- Darmowe papierowe modele czworościanu i wielu innych wielościanów
- An Amazing, Space Filling, Non-regular Tetrahedron, który zawiera również opis „obracającego się pierścienia czworościanów”, znanego również jako kaleidocykl.
- Tetrahedron Core Network Zastosowanie struktury czworościanu do stworzenia odpornej sieci danych z częściowymi siatkami
- Dokładne wzory na tensor bezwładności dowolnego czworościanu w kategoriach jego współrzędnych wierzchołkowych
- Tensor bezwładności czworościanu
.