Mniej…
![]()
Istnieje wiele wzorów ![]() wielu typów. Między innymi są to szeregi, iloczyny, konstrukcje geometryczne, granice, wartości specjalne i iteracje pi.
wielu typów. Między innymi są to szeregi, iloczyny, konstrukcje geometryczne, granice, wartości specjalne i iteracje pi.
![]() jest ściśle związane z własnościami okręgów i sfer. Dla okręgu o promieniu
jest ściśle związane z własnościami okręgów i sfer. Dla okręgu o promieniu ![]() , obwód i pole są dane przez
, obwód i pole są dane przez
|
(1)
|
|||
|
(2)
|
Podobnie, dla kuli o promieniu ![]() , pole powierzchni i objętość zamknięta wynoszą
, pole powierzchni i objętość zamknięta wynoszą
|
(3)
|
|||
|
(4)
|
Dokładnym wzorem na ![]() w postaci odwrotnych tangensów ułamków jednostkowych jest wzór Machina
w postaci odwrotnych tangensów ułamków jednostkowych jest wzór Machina
|
(5)
|
Istnieją jeszcze trzy inne wzory podobne do wzoru Machina, a także tysiące innych podobnych wzorów o większej liczbie wyrażeń.
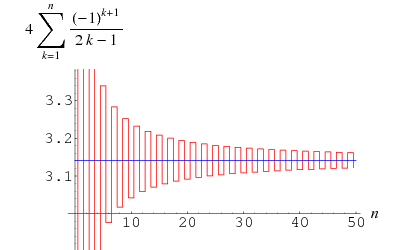
Gregory i Leibniz znaleźli
|
(6)
|
|||
|
(7)
|
(Wells 1986, s. 50), który jest znany jako szereg Gregory’ego i może być otrzymany przez wstawienie ![]() do szeregu Leibniza dla
do szeregu Leibniza dla ![]() . Błąd po
. Błąd po ![]() tym wyrazie tego szeregu w szeregu Gregory’ego jest większy niż
tym wyrazie tego szeregu w szeregu Gregory’ego jest większy niż ![]() , więc suma ta zbiega się tak wolno, że 300 wyrazów nie wystarczy do prawidłowego obliczenia
, więc suma ta zbiega się tak wolno, że 300 wyrazów nie wystarczy do prawidłowego obliczenia ![]() z dokładnością do dwóch miejsc po przecinku! Można to jednak przekształcić do postaci
z dokładnością do dwóch miejsc po przecinku! Można to jednak przekształcić do postaci
|
(8)
|
gdzie ![]() jest funkcją zeta Riemanna (Vardi 1991, str. 157-158; Flajolet i Vardi 1996), tak że błąd po
jest funkcją zeta Riemanna (Vardi 1991, str. 157-158; Flajolet i Vardi 1996), tak że błąd po ![]() terminach wynosi
terminach wynosi ![]() .
.
Seria sum nieskończonych Abrahama Sharpa (ok. 1717) jest dany przez
|
(9)
|
(Smith 1953, s. 311). Dodatkowe proste szeregi, w których pojawia się ![]() to
to
|
(10)
|
|||
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
|||
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
(Wells 1986, s. 53).
W 1666 r, Newton wykorzystał konstrukcję geometryczną do wyprowadzenia wzoru
|
(18)
|
|||
|
(19)
|
które wykorzystał do obliczenia ![]() (Wells 1986, s. 50; Borwein et al. 1989; Borwein i Bailey 2003, s. 105-106). Współczynniki można znaleźć z całki
(Wells 1986, s. 50; Borwein et al. 1989; Borwein i Bailey 2003, s. 105-106). Współczynniki można znaleźć z całki
|
(20)
|
|||
|
(21)
|
wykonując rozwinięcie szeregowe ![]() wokół 0, obtaining
wokół 0, obtaining
|
(22)
|
(OEIS A054387 i A054388). Zastosowanie przekształcenia Eulera poprawiającego zbieżność daje
|
(23)
|
|||
|
(24)
|
|||
|
(25)
|
(Beeler et al. 1972, poz. 120).
Odpowiada to wstawieniu ![]() w szereg potęgowy dla funkcji hipergeometrycznej
w szereg potęgowy dla funkcji hipergeometrycznej ![]() ,
,
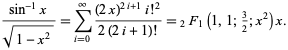 |
(26)
|
Mimo poprawy zbieżności, szereg (◇) zbiega tylko na jednym bicie/terminie. Kosztem pierwiastka kwadratowego, Gosper zauważył, że ![]() daje 2 bity/termin,
daje 2 bity/termin,
|
(27)
|
i ![]() daje prawie 3.39 bitów/termin,
daje prawie 3.39 bitów/termin,
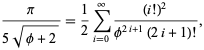 |
(28)
|
gdzie ![]() jest złotą proporcją. Gosper otrzymał również
jest złotą proporcją. Gosper otrzymał również
|
(29)
|
Algorytm spigot dla ![]() podają Rabinowitz i Wagon (1995; Borwein i Bailey 2003, s. 141-142).
podają Rabinowitz i Wagon (1995; Borwein i Bailey 2003, s. 141-142).
Jeszcze bardziej zdumiewające jest to, że wyrażenie w formie zamkniętej dające algorytm ekstrakcji cyfr, który produkuje cyfry ![]() (lub
(lub ![]() ) w bazie 16 zostało odkryte przez Bailey et al. (Bailey et al. 1997, Adamchik and Wagon 1997),
) w bazie 16 zostało odkryte przez Bailey et al. (Bailey et al. 1997, Adamchik and Wagon 1997),
|
(30)
|
Ta formuła, znana jako formuła BBP, została odkryta przy użyciu algorytmu PSLQ (Ferguson et al. 1999) i jest równoważna
|
(31)
|
Istnieje szereg wzorów typu BBP na ![]() w potęgach
w potęgach ![]() , z których pierwsze kilka niezależnych wzorów to
, z których pierwsze kilka niezależnych wzorów to
|
(32)
|
|||
|
(33)
|
|||
|
(34)
|
|||
 |
(35)
|
||
 |
(36)
|
||
 |
(37)
|
Podobnie, istnieje szereg wzorów typu BBP dla ![]() w potęgach
w potęgach ![]() , z których kilka pierwszych niezależnych wzorów to
, z których kilka pierwszych niezależnych wzorów to
|
(38)
|
||||
|
(39)
|
||||
 |
(40)
|
|||
 |
(41)
|
|||
 |
(42)
|
|||
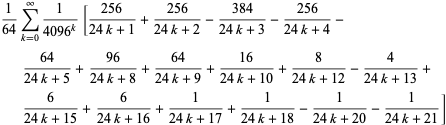 |
(43)
|
|||
 |
(44)
|
|||
 |
(45)
|
(45)
|
||
 |
(46)
|
|||
 |
(47)
|
|||
 |
(48)
|
F. Bellard znalazł szybko zbieżną formułę typu BBP
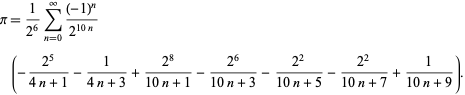 |
(49)
|
Pokrewną całką jest
|
(50)
|
(Dalzell 1944, 1971; Le Lionnais 1983, s. 22; Borwein, Bailey, and Girgensohn 2004, s. 3; Boros i Moll 2004, s. 125; Lucas 2005; Borwein et al. 2007, s. 14). Ta całka była znana przez K. Mahlera w połowie lat 60. i pojawia się w egzaminie na Uniwersytecie w Sydney w listopadzie 1960 roku (Borwein, Bailey i Girgensohn, s. 3). Beukers (2000) oraz Boros i Moll (2004, s. 126) stwierdzają, że nie jest jasne, czy istnieje naturalny wybór wielomianu racjonalnego, którego całka od 0 do 1 daje ![]() , gdzie 333/106 jest kolejną zbieżną. Istnieje jednak całka dla czwartej zbieżnej, mianowicie
, gdzie 333/106 jest kolejną zbieżną. Istnieje jednak całka dla czwartej zbieżnej, mianowicie
|
(51)
|
(Lucas 2005; Bailey et al. 2007, s. 219). W rzeczywistości, Lucas (2005) podaje kilka innych takich całek.
Backhouse (1995) użył tożsamości
|
(52)
|
|||
|
(53)
|
|||
|
(54)
|
dla dodatnich liczb całkowitych ![]() i
i ![]() oraz gdzie
oraz gdzie ![]() ,
, ![]() , oraz
, oraz ![]() są racjonalnymi stałymi, aby wygenerować pewną liczbę wzorów na
są racjonalnymi stałymi, aby wygenerować pewną liczbę wzorów na ![]() . W szczególności, jeśli
. W szczególności, jeśli ![]() , to
, to ![]() (Lucas 2005).
(Lucas 2005).
Podobny wzór został następnie odkryty przez Fergusona, prowadząc do dwuwymiarowej siatki takich formuł, która może być wygenerowana przez te dwie formuły dane przez
|
(55)
|
dla dowolnej wartości złożonej ![]() (Adamczyk i Wagon), dając wzór BBP jako szczególny przypadek
(Adamczyk i Wagon), dając wzór BBP jako szczególny przypadek ![]() .
.
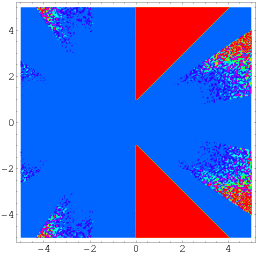
Jeszcze bardziej ogólna tożsamość zawdzięczana Wagonowi jest dana przez
 |
(56)
|
(Borwein i Bailey 2003, p. 141), która obowiązuje na obszarze płaszczyzny zespolonej z wyłączeniem dwóch trójkątnych części symetrycznie umieszczonych wokół osi rzeczywistej, jak pokazano powyżej.
Być może jeszcze dziwniejsza ogólna klasa tożsamości jest dana przez
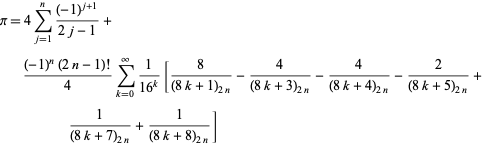 |
(57)
|
która zachodzi dla dowolnej dodatniej liczby całkowitej ![]() , gdzie
, gdzie ![]() jest symbolem Pochhammera (B. Cloitre, pers. comm., Jan. 23, 2005). Co jeszcze bardziej zdumiewające, istnieje ściśle analogiczny wzór na logarytm naturalny z 2.
jest symbolem Pochhammera (B. Cloitre, pers. comm., Jan. 23, 2005). Co jeszcze bardziej zdumiewające, istnieje ściśle analogiczny wzór na logarytm naturalny z 2.
Po odkryciu wzoru BBP na 16 cyfr podstawy i pokrewnych wzorów, zaczęto badać podobne wzory w innych podstawach. Borwein, Bailey i Girgensohn (2004) pokazali ostatnio, że ![]() nie ma formuły arctangensa BBP typu Machina, która nie jest binarna, choć nie wyklucza to zupełnie innego schematu dla algorytmów ekstrakcji cyfr w innych bazach.
nie ma formuły arctangensa BBP typu Machina, która nie jest binarna, choć nie wyklucza to zupełnie innego schematu dla algorytmów ekstrakcji cyfr w innych bazach.
S. Plouffe opracował algorytm obliczania ![]() cyfry z
cyfry z ![]() w dowolnej bazie w
w dowolnej bazie w ![]() krokach.
krokach.
Szeroki zestaw dodatkowych tożsamości należnych Ramanujanowi, Catalanowi i Newtonowi jest podany przez Castellanosa (1988ab, str. 86-88), w tym kilka dotyczących sum liczb Fibonacciego. Ramanujan znalazł
 |
(58)
|
(Hardy 1923, 1924, 1999, p. 7).
Plouffe (2006) znalazł piękny wzór
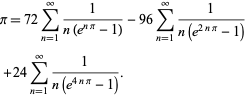 |
(59)
|
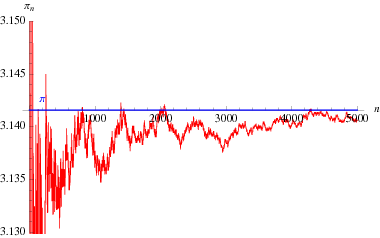
Ciekawy wzór na iloczyn nieskończony zawdzięczany Eulerowi, który dotyczy ![]() i
i ![]() liczby pierwszej
liczby pierwszej ![]() to
to
 |
(60)
|
||
|
(61)
|
(Blatner 1997, p. 119), wykreślony powyżej jako funkcja liczby wyrazów w iloczynie.
Metodę podobną do metody Archimedesa można zastosować do oszacowania ![]() zaczynając od
zaczynając od ![]() gonu, a następnie odnosząc pole kolejnych
gonu, a następnie odnosząc pole kolejnych ![]() gonów. Niech
gonów. Niech ![]() będzie kątem poprowadzonym ze środka jednego z odcinków wielokąta,
będzie kątem poprowadzonym ze środka jednego z odcinków wielokąta,
|
(62)
|
to
|
(63)
|
(Beckmann 1989, pp. 92-94).
Vieta (1593) jako pierwszy podał dokładne wyrażenie na ![]() przyjmując
przyjmując ![]() w powyższym wyrażeniu, dając
w powyższym wyrażeniu, dając
|
(64)
|
co prowadzi do nieskończonego iloczynu zagnieżdżonych radykalnych,
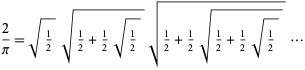 |
(65)
|
(Wells 1986, s. 50; Beckmann 1989, s. 95). Jednak rygorystycznie udowodniono zbieżność tego wyrażenia dopiero u Rudio w 1892 roku.
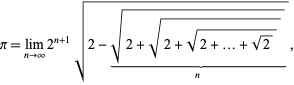
Pokrewny wzór jest dany przez
 |
(66)
|
którą można zapisać
|
(67)
|
gdzie ![]() jest zdefiniowane za pomocą iteracji
jest zdefiniowane za pomocą iteracji
 |
(68)
|
z ![]() (J. Munkhammar, pers. comm., 27 kwietnia 2000 r.). Wzór
(J. Munkhammar, pers. comm., 27 kwietnia 2000 r.). Wzór
 |
(69)
|
jest również blisko spokrewniona.
Piękny wzór na ![]() jest dany przez
jest dany przez
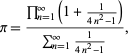 |
(70)
|
gdzie licznik jest postacią wzoru Wallisa dla ![]() , a mianownik jest sumą teleskopową z sumą 1/2, gdyż
, a mianownik jest sumą teleskopową z sumą 1/2, gdyż
|
(71)
|
(Sondow 1997).
Szczególny przypadek wzoru Wallisa daje
|
(72)
|
(Wells 1986, s. 50). Wzór ten można również zapisać
 |
(73)
|
gdzie ![]() oznacza współczynnik dwumianowy, a
oznacza współczynnik dwumianowy, a ![]() jest funkcją gamma (Knopp 1990). Euler otrzymał
jest funkcją gamma (Knopp 1990). Euler otrzymał
|
(74)
|
co wynika ze szczególnej wartości funkcji zeta Riemanna ![]() . Podobne wzory wynikają z
. Podobne wzory wynikają z ![]() dla wszystkich liczb całkowitych dodatnich
dla wszystkich liczb całkowitych dodatnich ![]() .
.
Suma nieskończona zawdzięczana Ramanujanowi to
|
(75)
|
(Borwein et al. 1989; Borwein i Bailey 2003, s. 109; Bailey et al.2007, s. 44). Dalsze sumy są podane u Ramanujana (1913-14),
|
(76)
|
i
|
(77)
|
|||
|
(78)
|
(Beeler et al. 1972, poz. 139; Borwein et al. 1989; Borwein i Bailey 2003, s. 108; Bailey et al. 2007, s. 44). Równanie (78) jest wyprowadzone z tożsamości modularnej rzędu 58, choć pierwsze wyprowadzenie nie zostało przedstawione przed Borwein i Borwein (1987). Powyższe serie dają
|
(79)
|
(Wells 1986, s. 54) jako pierwsze przybliżenie i zapewniają, odpowiednio, około 6 i 8 miejsc po przecinku na każdy człon. Szeregi takie istnieją ze względu na racjonalność różnych niezmienników modularnych.
Ogólna postać szeregu to
|
(80)
|
gdzie ![]() jest wyróżnikiem binarnej formy kwadratowej,
jest wyróżnikiem binarnej formy kwadratowej, ![]() jest funkcją j,
jest funkcją j,
|
(81)
|
|||
|
(82)
|
i ![]() są szeregami Eisensteina. W polu o numerze klasy
są szeregami Eisensteina. W polu o numerze klasy ![]() występują
występują ![]() całkowite liczby algebraiczne stopnia o stałych
całkowite liczby algebraiczne stopnia o stałych ![]() ,
, ![]() i
i ![]() . Spośród wszystkich szeregów składających się tylko z wyrazów całkowitych, ten dający najwięcej cyfr liczbowych w najkrótszym czasie odpowiada największemu wyróżnikowi klasy numer 1
. Spośród wszystkich szeregów składających się tylko z wyrazów całkowitych, ten dający najwięcej cyfr liczbowych w najkrótszym czasie odpowiada największemu wyróżnikowi klasy numer 1 ![]() i został sformułowany przez braci Chudnovsky (1987). Występująca tu liczba 163 jest tą samą, która pojawia się w fakcie, że
i został sformułowany przez braci Chudnovsky (1987). Występująca tu liczba 163 jest tą samą, która pojawia się w fakcie, że ![]() (stała Ramanujana) jest bardzo blisko liczby całkowitej. Podobnie, czynnik
(stała Ramanujana) jest bardzo blisko liczby całkowitej. Podobnie, czynnik ![]() pochodzi z tożsamości funkcji j dla
pochodzi z tożsamości funkcji j dla ![]() . Szereg jest dany przez
. Szereg jest dany przez
|
(83)
|
|||
|
(84)
|
(Borwein i Borwein 1993; Beck i Trott; Bailey et al. 2007, s. 44). Szereg ten daje 14 cyfr dokładnie na jeden człon. To samo równanie w innej formie zostało podane przez braci Chudnovsky (1987) i jest używane przez język Wolfram do obliczania ![]() (Vardi 1991; Wolfram Research),
(Vardi 1991; Wolfram Research),
|
(85)
|
gdzie
|
(86)
|
|||
|
(87)
|
|||
|
(88)
|
Najlepszy wzór dla klasy numer 2 (największa wyróżnialność ![]() ) to
) to
|
(89)
|
gdzie
|
(90)
|
|||
|
(91)
|
|||
|
(92)
|
(Borwein i Borwein 1993). Ten szereg dodaje około 25 cyfr dla każdego dodatkowego członu. Najszybciej zbieżna seria dla klasy numer 3 odpowiada ![]() i daje 37-38 cyfr na każdy termin. Najszybciej zbieżny szereg dla klasy numer 4 odpowiada
i daje 37-38 cyfr na każdy termin. Najszybciej zbieżny szereg dla klasy numer 4 odpowiada ![]() i wynosi
i wynosi
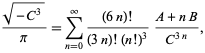 |
(93)
|
gdzie
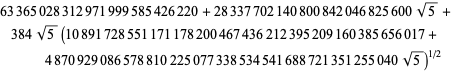 |
(94)
|
||
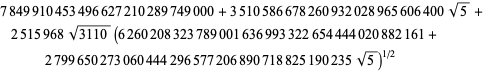 |
(95)
|
||
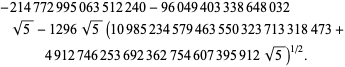 |
(96)
|
Daje to 50 cyfr na termin. Borwein i Borwein (1993) opracowali ogólny algorytm generowania takich serii dla dowolnego numeru klasy.
Kompletne zestawienie serii Ramanujana dla ![]() znalezionych w jego drugim i trzecim zeszycie podaje Berndt (1994, s. 352-354),
znalezionych w jego drugim i trzecim zeszycie podaje Berndt (1994, s. 352-354),
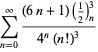 |
(97)
|
||
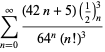 |
(98)
|
||
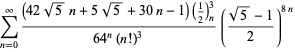 |
(99)
|
||
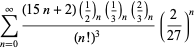 |
(100)
|
||
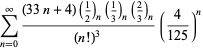 |
(101)
|
||
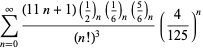 |
(102)
|
||
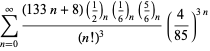 |
(103)
|
||
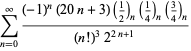 |
(104)
|
||
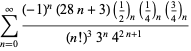 |
(105)
|
||
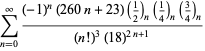 |
(106)
|
||
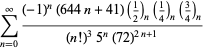 |
(107)
|
||
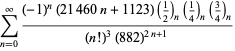 |
(108)
|
||
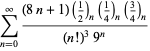 |
(109)
|
||
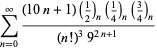 |
(110)
|
||
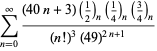 |
(111)
|
||
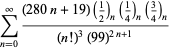 |
(112)
|
||
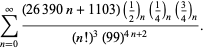 |
(113)
|
Równania te zostały po raz pierwszy udowodnione przez Borweina i Borwein (1987a, s. 177-187). Borwein i Borwein (1987b, 1988, 1993) udowodnili inne równania tego typu, a Chudnovsky i Chudnovsky (1987) znaleźli podobne równania dla innych stałych transcendentalnych (Bailey et al. 2007, s. 44-45).
Pełna lista niezależnych znanych równań tego typu jest podana
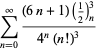 |
(114)
|
||
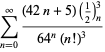 |
(115)
|
||
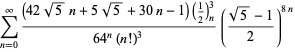 |
(116)
|
||
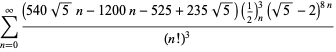 |
(117)
|
||
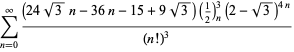 |
(118)
|
dla ![]() z niezmienniczymi znakami,
z niezmienniczymi znakami,
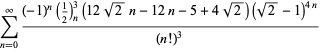 |
(119)
|
||
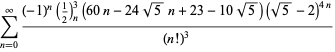 |
(120)
|
||
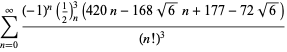 |
(121)
|
||
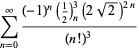 |
(122)
|
dla ![]() z naprzemiennymi znakami,
z naprzemiennymi znakami,
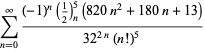 |
(123)
|
||
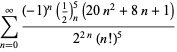 |
(124)
|
dla ![]() (Guillera 2002, 2003, 2006),
(Guillera 2002, 2003, 2006),
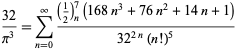 |
(125)
|
dla ![]() (Guillera 2002, 2003, 2006), a żadne inne dla
(Guillera 2002, 2003, 2006), a żadne inne dla ![]() nie są znane (Bailey i in. 2007, s. 45-48).
nie są znane (Bailey i in. 2007, s. 45-48).
Bellard podaje egzotyczny wzór
 |
(126)
|
where
|
(127)
|
Gasper przytacza wynik
|
(128)
|
gdzie ![]() jest uogólnioną funkcją hipergeometryczną, i przekształca go na
jest uogólnioną funkcją hipergeometryczną, i przekształca go na
|
(129)
|
Fascynujący wynik zawdzięczamy Gosperowi
|
(130)
|
![]() spełnia nierówność
spełnia nierówność
|
(131)
|
D. Terr (pers. comm.) zauważył osobliwą tożsamość
|
(132)
|
zawierającą pierwsze 9 cyfr liczby pi.
.