AC, ou corrente alternada, é assim chamada porque a corrente alterna ou gira para trás e para a frente entre duas polaridades. Em outras palavras, a corrente (e consequentemente a tensão) é uma função do tempo. Isto é fundamentalmente diferente da corrente contínua que é fixa em polaridade e geralmente constante ao longo do tempo. Uma fonte de tensão contínua de laboratório, por exemplo, idealmente mantém uma tensão definida através dos seus terminais e não varia ao longo do tempo. Em contraste, à medida que uma forma de onda alternada vai e vem através do tempo, a sua forma pode exibir grandes variações que vão desde os caminhos simples e regulares dos padrões de laboratório, tais como ondas senoidais, ondas triangulares e ondas quadradas, até às formas de onda muito mais complexas e onduladas produzidas por instrumentos musicais e pela voz humana.
A onda senoidal é a onda mais simples que pode ser criada. Ela representa o movimento de um simples vetor girando a uma velocidade constante, como o deslocamento vertical do ponteiro dos segundos de um relógio. Um exemplo é mostrado na Figura \PageIndex{1}}). O eixo horizontal plota o tempo. Ele aumenta conforme nos movemos da esquerda para a direita (isto é, se o ponto A está à direita do ponto B, então A ocorre mais tarde do que B). O eixo vertical é representado aqui em geral como uma percentagem do máximo mas normalmente seria uma medida de tensão, corrente, pressão sonora, ou semelhante.
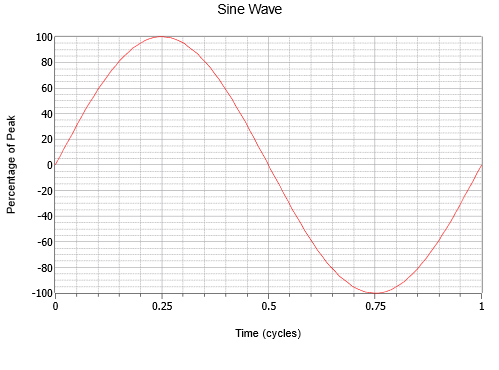
Figure {1}(\PageIndex{1}}): Uma onda sinusoidal.
Nota a variação suave que começa em zero, sobe para um pico positivo um quarto de caminho, volta a zero a meio, continua para um pico negativo três quartos de caminho, e depois sobe novamente para onde começou. Este processo então se repete. Cada repetição é referida como um ciclo. Na Figura \PageIndex (1), um ciclo completo é mostrado.
Ondas sinusoidais exibem simetria de um quarto de onda. Ou seja, cada quarto (no tempo) da onda é idêntico a qualquer outro se você simplesmente gira-a em torno do eixo horizontal e/ou gira-a na vertical em relação ao seu pico. O tempo que leva para completar um ciclo é chamado de período e é denotado com o símbolo \ (T\) (para o Tempo). O recíproco do período é a freqüência, \(f\).
A freqüência indica quantos ciclos existem em um segundo. Para honrar um dos pesquisadores do século XIX na área, em vez de chamar a unidade de “ciclos por segundo”, usamos Hertz, nomeado em homenagem a Heinrich Hertz e abreviado Hz. Na Figura \PageIndex (2) são mostradas três ondas sinusoidais com frequências diferentes; a onda inicial (verde), uma onda com o dobro da frequência (azul), e uma terceira com metade da frequência ou o dobro do período (vermelho).
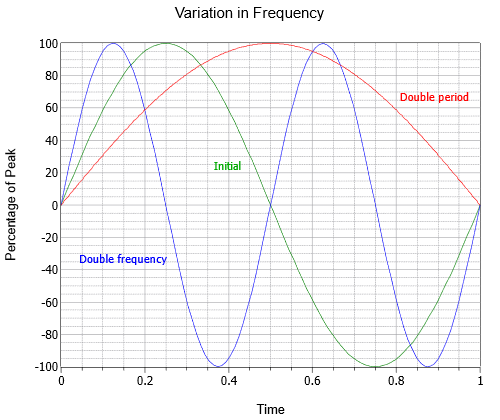
Figure \PageIndex (2)): Variação da frequência da onda sinusoidal.
A amplitude (vertical) da onda pode ser expressa como uma quantidade de pico, que é a mudança da linha zero central até ao valor mais positivo. A amplitude também pode ser expressa como pico a pico; a distância entre o mais negativo e o mais positivo. Para uma onda senoidal isto será sempre o dobro do valor de pico, embora possa não ser o caso para outras ondas que possam ser assimétricas. Uma série de três ondas sinusoidais com amplitudes diferentes são mostradas na Figura \PageIndex (3). Ao longo do lado as versões iniciais (verde) são de dupla amplitude (azul) e de meia amplitude (vermelho).
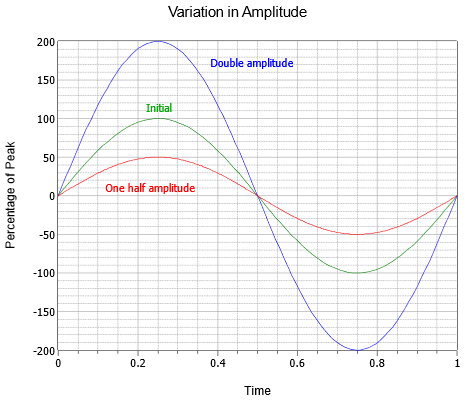
Figure \(\PageIndex{3}}): Variação de amplitude de onda sinusoidal.
Combinando estes parâmetros, considere a forma de onda de tensão mostrada na Figura \PageIndex{4}}. Aqui vemos dois ciclos de uma onda de tensão AC.
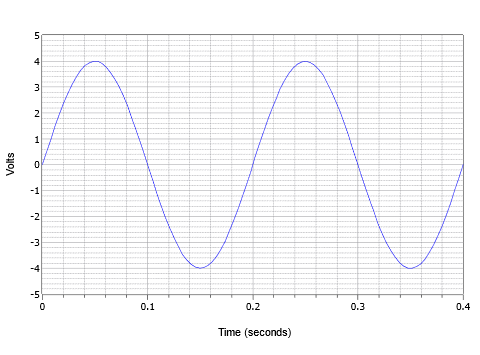
Figure \(\PageIndex{4}}): Exemplo básico de onda senoidal.
O valor de pico é 4 volts e o valor de pico a pico é 8 volts (tipicamente abreviado como “8 V pp”). O período de um ciclo é de 0,2 segundos, ou \(T = 200\) milissegundos. Além disso, a freqüência, \(f = 1/200\) milissegundos, ou 5 Hz (5 ciclos em um segundo).
AC formas de onda também podem ser combinados com um offset DC. A adição de um nível DC positivo desloca a onda para cima na vertical, enquanto um nível DC negativo desloca a onda para baixo na vertical. Isto não altera a frequência ou a parte AC da amplitude (embora os picos absolutos se desloquem pelo valor DC). A Figura 5 mostra o efeito de vários offsets DC. Acima da onda inicial (verde) é uma onda idêntica com um offset DC positivo igual a 20% do valor de pico original (azul). Abaixo do original está uma terceira onda (vermelha) que exibe um deslocamento DC negativo igual a metade do valor de pico do original.
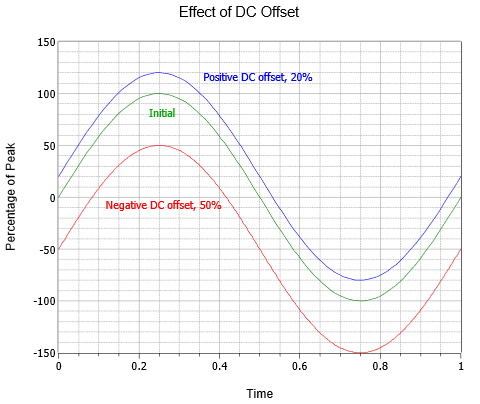
Figure \(\PageIndex{5}}): Variação do desvio da onda sinusoidal DC.
Outra, é possível que uma onda sinusoidal seja deslocada no tempo em comparação com alguma outra onda sinusoidal ou referência. Embora seja possível indicar esse deslocamento como um tempo absoluto, é mais comum fazê-lo como deslocamento de fase, ou seja, o tempo expresso como uma porção do período em graus. Por exemplo, se um seno está à frente de outro por um quarto do período, diz-se que está à frente por 90 (ou seja, 1/4 de 360). Se estiver atrasado por ½ do período, diz-se que está atrasado por 180 (i.e., mais tarde no tempo por 1/2 ciclo). Outra forma de afirmar isto é que as formas de onda principais começam mais cedo no tempo e assim são atraídas para a esquerda da referência, enquanto as formas de onda atrasadas começam mais tarde no tempo e são atraídas para a direita.
Figure {6}) ilustra o efeito do deslocamento de fase. Note que neste gráfico, \\(t = 0\) foi movido para o centro do eixo horizontal. A curva média é a onda inicial, ou de referência (verde). À esquerda (vermelho) é uma onda que conduz a onda inicial por um oitavo ciclo, ou 45 Para a direita (azul), é uma onda retardada pela metade, ou -22,5\(^{\circ}}).
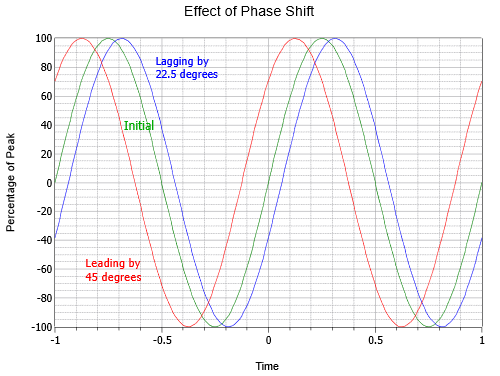
Figure {6}(PageIndex{6}}): Variação de fase de onda sinusoidal.
Combinando os elementos anteriores permite-nos desenvolver um formato geral para uma onda sinusoidal (tensão apresentada):
Onde
(v(t)\) é a voltagem em algum momento,
(V_{DC}}} é o offset DC, se houver,
(V_{P}}) é o valor de pico,
(f) é a frequência,
(theta) é o deslocamento de fase (+ se conduzindo e atraindo para a esquerda, – se atrasando e atraindo para a direita).
Para um exemplo rápido e prático, a forma de onda mostrada na Figura \PageIndex (4) tem uma amplitude de 4 volts de pico, uma frequência de 5 Hz, e sem deslocamento de fase ou deslocamento de corrente contínua. Assim, sua expressão é \(v(t) = 4 \sin (2 \pi 5 t)\)
Para calcular um deslocamento de fase, primeiro determine o diferencial de tempo entre a forma de onda e a referência, que chamaremos de \i(delta t). A referência pode ser um ponto fixo no tempo (por exemplo, \(t = 0\)) ou outra forma de onda. Geralmente, a maneira mais fácil de fazer isso é medir a diferença no cruzamento zero, assumindo que não haja offset DC. Se houver um deslocamento, faça a medição para onde a passagem de zero foi deslocada (isto é, no nível do deslocamento DC). Quando a diferença for encontrada, dividi-la pelo período para representar o deslocamento como uma fração de um período. Como um ciclo representa uma rotação do vetor, ou 360 graus, simplesmente multiplique a fração por 360 graus para encontrar o deslocamento de fase em graus. Expresso como uma fórmula:
\
Remember, se a onda é deslocada para a esquerda, então ela é líder e positiva, enquanto um deslocamento para a direita é retardado ou atrasado no tempo, e, portanto, negativo.
Exemplo \\(\PageIndex{1})
Escreva a expressão para a forma de onda mostrada na Figura \PageIndex{7}).
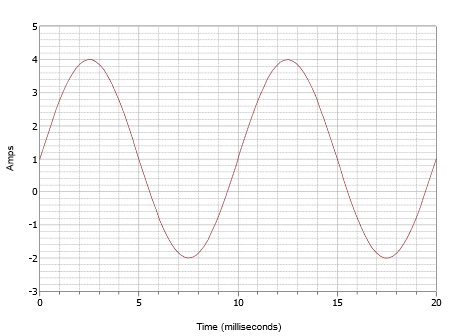
Figure \PageIndex{7}): Forma de onda por exemplo {1}(\PageIndex{1}}}2089>
Esta forma de onda superficialmente pode parecer-se com a da Figura {4}PageIndex{4}) mas não se deixe enganar por isto. Antes de mais nada, a escala de tempo é diferente. Para esta forma de onda, um ciclo se completa em 10 milissegundos. Portanto, a frequência é
A segunda questão é o offset DC. Note que o pico positivo ocorre a 4 amps enquanto o negativo ocorre a -2 amps. Isto indica um valor de pico a pico de 6 amps. Sem um offset, o pico positivo seria de 3 amps, portanto há um offset DC de +1 amps. O centro vertical da forma de onda é deslocado para cima de 0 amps para +1 amp. Este ponto está em t = 0, portanto, não há deslocamento de fase. A expressão resultante é:
Exemplo \(\PageIndex{2})
Escreva a expressão para a forma de onda mostrada na Figura \(\PageIndex{8}\).
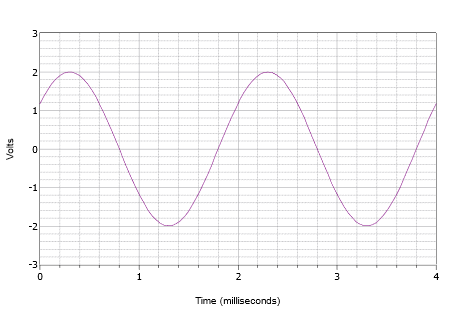
Figure \(\PageIndex{8}}): Waveform for Example \(\PageIndex{2}\).
First off, the positive peak is 2 volts and the peak-to-peak value is 4 volts. Portanto, não há offset DC. O centro vertical da onda não começa em \(t = 0\), portanto deve haver um deslocamento de fase. O valor em \(t = 0\) é de 1,2 volts. A onda atinge essa mesma amplitude em \(t = 2\) milissegundos e começa a repetir outro ciclo. Consequentemente, o período deve ser de 2 milissegundos. A freqüência é a recíproca deste valor, e assim \(f = 500\) Hz.
A forma de onda é deslocada para a esquerda, o que indica um deslocamento de fase positivo ou principal. Se examinarmos o segundo ciclo, vemos que ele atinge zero volts a 1,8 milissegundos. Portanto, o deslocamento é de 0,2 milissegundos. Expresso em graus isto é:
A expressão final é:
Exemplo \(\PageIndex{3})
Desenhar a forma de onda correspondente à seguinte expressão.
Primeiro, note que o offset de -3 volts empurra o pico positivo de 5 volts para 2 volts, e o negativo de -5 volts para -8 volts. A frequência de 40 kHz dita um período de:
O deslocamento de fase de -72\(^{\circ}}) representa 72/360, ou 0,2 ciclos. Isto corresponde a um atraso de tempo (deslocado para a direita porque é negativo) de 0,2 vezes 25 s, ou 5 s.
Inicialmente, muitas vezes é melhor construir a trama através de uma série de passos discretos em vez de tentar desenhar tudo de uma só vez. Primeiro, desenhe uma onda sinusoidal com uma amplitude de pico de 5 volts e um período de 25 mu(mu)s. Agora, empurre a forma de onda para baixo 3 volts para que o pico positivo seja apenas 2 volts e o pico negativo para baixo a -8 volts. Finalmente, empurre a onda recém-deslocada para a direita por 5mu’s. O resultado é mostrado na Figura \PageIndex (9).
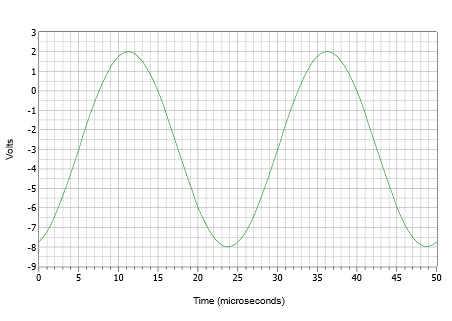
Figure \PageIndex (9)): Forma de onda por exemplo \(\PageIndex{3}\).
1.2.1: Medidas de laboratório
No laboratório, um gerador de funções é usado para gerar pecados e outras formas de ondas. Estes dispositivos permitirão um controle preciso sobre a amplitude e frequência da onda juntamente com a adição de um offset DC, se desejado. Um exemplo é mostrado na Figura \PageIndex{10}). A ferramenta de medição correspondente é o osciloscópio, ou apenas o escopo, para abreviar.

Figure \(\PageIndex{10}}): Gerador de sinal de laboratório.
O osciloscópio é talvez o dispositivo de medição mais útil e versátil do laboratório. Tipicamente, eles possuem dois ou quatro canais de entrada, embora mais sejam possíveis. Cada canal de entrada tem seu próprio ajuste de sensibilidade e todos os canais compartilham uma referência de tempo comum. O visor desenha formas de onda da mesma maneira que aquelas vistas nas figuras {1}(PageIndex{9}) -(PageIndex{9}). Além disso, eles podem traçar uma voltagem contra outra (modo X – Y). Os osciloscópios modernos têm características adicionais como a medição automática de freqüência, amplitude, deslocamento de fase, etc., medições baseadas em cursor, e a capacidade de salvar imagens como arquivos gráficos. Um exemplo de um osciloscópio digital de quatro canais é mostrado na Figura \(\PageIndex{11}\).

Figure \(\PageIndex{11}}): Um osciloscópio digital.
1.2.2: Símbolos esquemáticos
No que diz respeito aos esquemas, os símbolos das fontes de tensão e corrente AC são mostrados na Figura \PageIndex{12}}. As marcações de polaridade e direção não são absolutas; afinal, são fontes CA cuja polaridade e direção giram para frente e para trás. Os marcadores são usados para estabelecer uma referência de tempo, especialmente em circuitos que empregam múltiplas fontes.
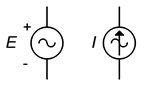
Figure \\(\PageIndex{12}}): Símbolos esquemáticos para fonte de tensão CA (esquerda) e fonte de corrente (direita).
Vale lembrar que negar uma fonte é o mesmo que inverter a sua polaridade. Isto foi verdade para fontes DC e continua a ser verdade para fontes AC. Isto é ilustrado na Figura \PageIndex{13}). Às vezes inverter ou negar uma fonte tornará a análise um pouco mais óbvia ou mais fácil de visualizar.
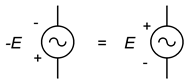
Figure {13}(\PageIndex{13}}): Equivalência de polaridade/sinal.
Exemplo \(\PageIndex{4}})
Conceitua que um osciloscópio exibe duas ondas como ilustrado na Figura \PageIndex{14}}. Determine o deslocamento de fase do pico de onda menor de 20 volts (azul) em relação ao pico de onda maior de 25 volts (vermelho).
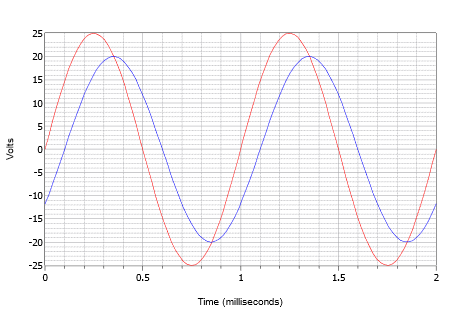
Figure \\(\PageIndex{14}}): Formas de onda por exemplo \(\PageIndex{4}\).
Primeiro, note que nenhuma das ondas exibe um offset DC. Se uma ou ambas tivessem um offset, a(s) onda(s) teria(teriam) de ser deslocadas verticalmente para que os seus pontos normais de intersecção zero estivessem no mesmo nível. Medindo qualquer uma das ondas, o período é encontrado em 1 milissegundo. A mudança de hora mais facilmente pode ser encontrada em qualquer um dos pontos de intersecção zero (há quatro locais para escolher). O atraso é um pequeno desvio, ou 0,1 milissegundos, com a onda menor atrasada no tempo, ou atrasada a onda maior. Isto indica um deslocamento de fase negativo.
\\
\
\
1.2.3: Sines e Cosines
Há um punhado de turnos de fase específicos que vale a pena ver mais de perto. Se uma onda sinusoidal for invertida, isto é, virada de cabeça para baixo, ela é indistinguível de uma onda sinusoidal que tenha sido deslocada +180 ou -180 graus. Em outras palavras, uma onda desse tipo pode ser escrita de três maneiras diferentes: \(-sin (2 pés de pí)), (2 pés de pí – 180^^circ), ou (2 pés de pí + 180^circ). Além disso, se uma onda sinusoidal é deslocada por +90 graus (ou seja, que leva e para a esquerda), também pode ser referida como uma onda co-seno. Assim, (2 {\pi ft + 90^{\circ}) = cos (2 {\pi ft)^). Finalmente, se uma onda sinusoidal é deslocada por -90 graus (ou seja, atrasada e para a direita), pode ser referida como uma onda cosseno negativa ou invertida. Assim, (2 {sin (2 {pi ft – 90^{\i1}) = -cos (2 {pi ft)}). As relações destas quatro ondas estão ilustradas na Figura {\PageIndex{15}}.
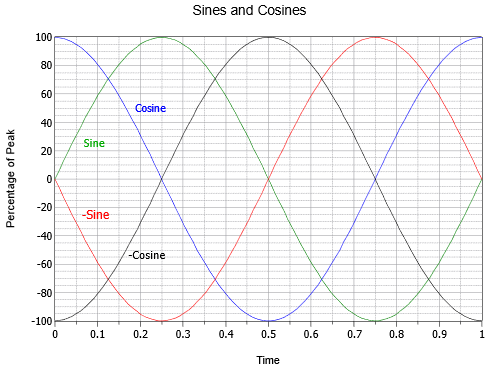
Figure {\PageIndex{15}): Relações temporais entre pecados e cossenos.
É importante notar também que a onda cossena representa a primeira derivada, ou inclinação, da onda senoidal. Como você deve se lembrar de outros estudos, a inclinação ou “declive” de uma linha é a razão entre a mudança vertical e a mudança horizontal, às vezes chamada “a elevação ao longo da corrida”. Para uma voltagem, seria a mudança de voltagem sobre a mudança no tempo, ou “delta V/ delta t”. Para uma curva de mudança suave e contínua como uma onda sinusoidal, a inclinação em um determinado ponto é definida apropriadamente como a primeira derivada, ou, neste caso, dv/dt. Para verificar se isto é verdade visualmente, note que a parte mais íngreme da onda sinusoidal (verde) é onde ela cruza amplitude zero. Como ela atravessa zero enquanto se movimenta positivamente (em \(t = 0\) ou \(t = 1\) na Figura 15), o cosseno (azul) está no seu pico positivo. Como o seno cruza zero enquanto se move negativamente (em \(t = 0,5\)), o cosseno está no seu pico negativo. Além disso, a onda sinusoidal é plana com uma inclinação de zero nos seus picos positivo e negativo (em \(t = 0,25\) e \(t = 0,75\), respectivamente), e nesses momentos a amplitude do cosseno também é zero. Também é verdade que a onda seno é a inclinação da onda cosseno negativa, o cosseno negativo é a inclinação do seno negativo, e o seno negativo é a inclinação do cosseno. Movendo-se na direcção inversa, podemos dizer que o anti-derivado (integral indefinido) de uma onda cosseno é uma onda senoidal, o integral de uma onda seno é uma onda cosseno negativa, e assim por diante. Estas relações revelar-se-ão mais úteis quando voltamos a nossa atenção para a resposta dos condensadores e indutores em circuitos AC.
1.2.4: RMS – Root Mean Square Measurement
Along with peak and peak-to-peak, amplitude pode ser dada como um valor RMS (Root Mean Square). Na verdade, se o pico ou pico a pico não for especificado, a medição é assumida como RMS. RMS é um cálculo especial utilizado para encontrar potência DC equivalente (muito comum, por exemplo, com amplificadores de potência de áudio). Em outras palavras, se estamos interessados em encontrar a potência em um resistor, o cálculo deve ser feito usando valores RMS para tensão ou corrente, e não valores de pico ou pico a pico. Não o fazer resultará em potências erradas. Isto é verdade independentemente da forma das ondas; seja uma onda senoidal, uma onda triangular ou as ondas complexas dos sinais musicais. Se uma tensão for especificada como RMS, ela pode ser tratada para cálculos de potência da mesma forma que uma tensão DC de tamanho equivalente. Por exemplo, uma RMS senoidal de 1 volt produzirá a mesma dissipação de energia e aquecimento em uma determinada resistência que uma DC de 1 volt. Por esta razão, RMS é às vezes referido como o valor efetivo (isto é, valor DC efetivo).
O nome root-mean-square descreve o processo de determinação do valor efetivo. Primeiro, lembre-se de que a potência é proporcional ao quadrado da voltagem ou corrente. Assim, o nosso primeiro passo será a quadratura da forma de onda de entrada. Claro, a forma de onda é uma função do tempo e o seu quadrado irá produzir uma nova forma. Neste ponto, precisamos de encontrar o valor médio desta nova forma. A razão para isso é simples, mas não necessariamente óbvia. Os componentes eléctricos e electrónicos têm massa e, portanto, não aquecem nem arrefecem instantaneamente. Eles exibem uma constante de tempo térmica. Portanto, eles respondem à média de entrada ao longo do tempo. Embora pudéssemos calcular alguma forma de “potência de pico instantânea” em algum instante específico no tempo, ela não representa a potência DC equivalente. Uma vez obtido o valor médio desta forma de onda quadrada, o valor DC correspondente é apenas a raiz quadrada da média. O resultado é um valor fracionário entre zero e um que é usado como fator de escala para transformar um valor de pico em um valor RMS. O valor será exclusivo para a forma de onda específica. Ou seja, todos os pecados (independentemente da fase) têm o mesmo fator, todas as ondas triangulares regulares têm o mesmo fator, e assim por diante. Como nos preocupamos principalmente com os pecados, vamos dar uma olhada mais de perto na determinação do fator RMS para eles.
Comecemos com a expressão básica para uma onda senoidal sem offset DC ou deslocamento de fase, e com uma amplitude de um:
O primeiro passo é ajustar esta forma de onda. Uma identidade trigonométrica útil é
\\
Aplicando isto aos nossos rendimentos de onda:
\
Esta expressão descreve uma onda cosseno invertida com o dobro da frequência original e metade da amplitude original, pedalando sobre um offset DC igual ao seu valor de pico. Em outras palavras, o pico negativo da cosseno está em zero e o pico positivo em 1. O próximo passo é encontrar a média ou valor médio deste resultado intermediário. A média é igual ao offset de 0,5. Isto pode ser visualizado como a área acima do offset preenchendo perfeitamente o “dip” abaixo do offset. O passo final é pegar a raiz quadrada da média. A raiz quadrada de 0,5 é igual a uma sobre a raiz quadrada de duas, ou aproximadamente 0,707. Portanto, o valor RMS é 0,707 vezes o pico. Alternativamente, você poderia dividir o pico por raiz quadrada de dois, ou aproximadamente 1,414. Este processo é mostrado graficamente na Figura \PageIndex (16).
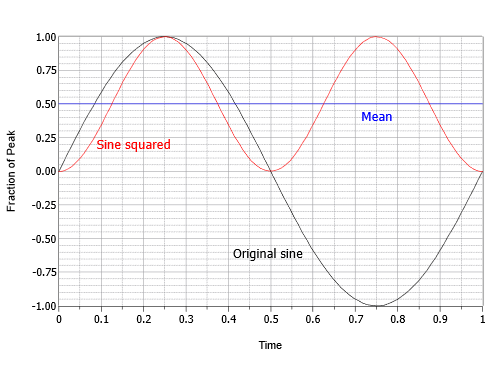
Figure \PageIndex (16)): Processo para encontrar o factor RMS para pecados.
Em suma, para ondas sinusoidais, RMS é sempre o valor de pico vezes 0,707. Podemos também dizer que o valor RMS de qualquer onda sinusoidal é o seu pico dividido por aproximadamente 1,414. Mais uma vez, estes rácios não seriam necessariamente verdadeiros para ondas não sinusoidais. Detalhes sobre outras formas comuns podem ser encontrados no Apêndice C. Finalmente, a razão entre o valor de pico e o valor RMS é chamada de razão de crista. Este é um valor fixo para ondas senoidais (novamente, cerca de 1,414), mas pode ser superior a 10:1 para alguns tipos de sinais de áudio.
1.2.5: Comprimento de onda
Outro item de interesse é a velocidade de propagação da onda. Isto varia muito. No caso da luz no vácuo (ou a uma aproximação próxima, uma corrente elétrica em um fio), a velocidade é de cerca de 3E8 metros por segundo (ou seja, 300.000 km/s) ou cerca de 186.000 milhas por segundo.
Dando uma velocidade e um período, podemos imaginar quão distantes estão os picos da onda. Esta distância é chamada de comprimento de onda e é denotada pela letra grega lambda (lambda). O comprimento de onda é igual à velocidade dividida pela frequência, (lambda = v/f). Assim, para um alto-falante produzindo um seno de 100 Hz, como a velocidade do som no ar é de 344 m/s, então, {lambda = 344 m/s, /, 100 } Hz, ou 3,44 metros (um pouco mais de 11 pés). Note que quanto maior a frequência, menor o comprimento de onda. Observe também que quanto mais rápida a velocidade, mais longo o comprimento de onda. Os cálculos do comprimento de onda são de particular importância nos campos das telecomunicações e acústica.