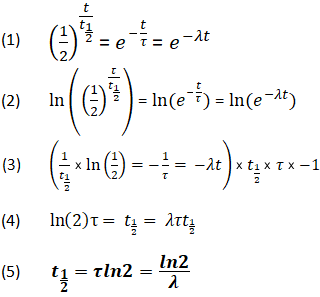As seguintes ferramentas podem gerar qualquer um dos valores dos outros três na fórmula de meia-vida para uma substância em decomposição diminuir pela metade.

Calculadora de meia-vida
Por favor, forneça qualquer um dos três seguintes para calcular o quarto valor.
Meia-vida, Tempo Médio de Vida e Conversão Constante de Decadência
Por favor forneça qualquer um dos seguintes para obter os outros dois.
Definição e Fórmula
Média-vida é definida como a quantidade de tempo que leva para que uma determinada quantidade diminua para metade do seu valor inicial. O termo é mais comumente usado em relação aos átomos em decaimento radioativo, mas pode ser usado para descrever outros tipos de decaimento, seja exponencial ou não. Uma das aplicações mais conhecidas da meia-vida é a datação por carbono-14. A meia-vida do carbono-14 é de aproximadamente 5.730 anos, e pode ser usada de forma confiável para medir datas até cerca de 50.000 anos atrás. O processo de datação por carbono-14 foi desenvolvido por William Libby, e é baseado no fato de que o carbono-14 está sendo feito constantemente na atmosfera. Ele é incorporado às plantas através da fotossíntese, e depois aos animais quando eles consomem plantas. O carbono-14 sofre decaimento radioativo quando a planta ou animal morre, e medir a quantidade de carbono-14 em uma amostra transmite informações sobre quando a planta ou animal morreu.
Below são mostradas três fórmulas equivalentes descrevendo o decaimento exponencial:
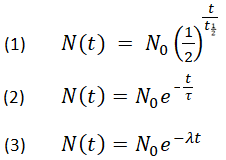
- onde
N0 é a quantidade inicial
Nt é a quantidade restante após o tempo, t
t1/2 é a meia-vida
τ é a vida média
λ é a constante de decaimento
Se um arqueólogo encontrou uma amostra fóssil que continha 25% de carbono-14 em comparação com uma amostra viva, a hora da morte da amostra fóssil poderia ser determinada pela equação de rearranjo 1, já que Nt, N0 e t1/2 são conhecidos.
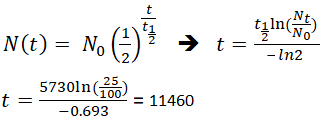
Isto significa que o fóssil tem 11.460 anos.
Derivação da Relação entre Constantes de Meia-Vida
Usando as equações acima, também é possível que uma relação seja derivada entre t1/2, τ e λ. Esta relação permite a determinação de todos os valores, desde que pelo menos um seja conhecido.