“Os homens falam de tempo de matar, enquanto o tempo os mata silenciosamente”
Dion Boucicault – London Assurance (1841)
- Até à data temos considerado a cinemática e dinâmica das partículas, incluindo o movimento translacional e circular, bem como o movimento translacional dos sistemas de partículas (em particular corpos rígidos) em termos do movimento do centro de massa do sistema (corpo). Neste último caso podemos imaginar que toda a massa do objecto está localizada no centro de massa no que diz respeito às forças translacionais externas.
-
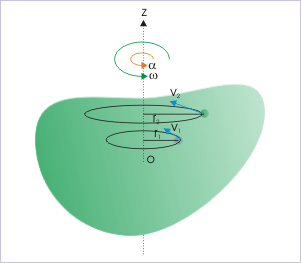O passo seguinte é considerar a rotação de um corpo rígido em torno de um eixo de rotação fixo. Note que, porque estamos considerando um corpo rígido, cada partícula do corpo permanece fixa em relação às outras. Isto significa que em tal movimento de rotação cada partícula se move em um círculo cujo centro está no eixo de rotação. No diagrama à direita o objeto gira em torno do eixo z; as duas partículas amostra se movem em círculos com raios r1 e r2. Se conseguirmos descrever o movimento circular de uma partícula, sem referência directa ao seu raio, então todas as partículas do sistema serão descritas pelo mesmo conjunto de equações. Embora os raios das partículas sejam diferentes, as suas rotações angulares são idênticas. Portanto, é necessário introduzir variáveis angulares.
- Medida radial dos ângulos
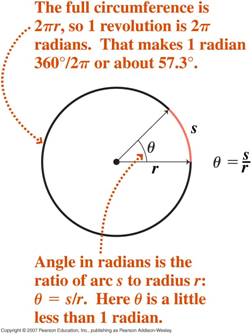
- Velocidade angular (Velocidade) e Aceleração angular
Avelocidade angular e aceleração angular são definidas de forma semelhante à velocidade e aceleração. Existem valores médios e instantâneos de cada um.
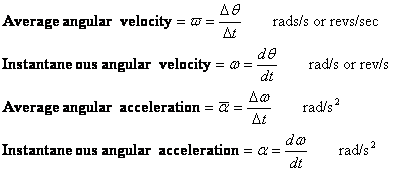
A aceleração angular não é o mesmo que a aceleração centrípeta. A aceleração centrípeta é devida a uma mudança na direção da velocidade, a aceleração angular é devida a uma mudança na magnitude da velocidade (através do ângulo de rotação).
>
Exatamente como no caso translacional, a diferença entre a velocidade angular e a velocidade angular é a direção. A velocidade angular deve incluir um sentido de rotação em torno do eixo em questão. Por exemplo, 10 rad/s no sentido horário sobre o eixo x é uma velocidade angular, 10 rad/s sobre o eixo x é uma velocidade angular.
- Equações Cinemáticas Rotacionais
>
Por analogia directa com as equações cinemáticas translacionais, o movimento circular em torno de um único eixo em aceleração angular constante pode ser descrito pelas quatro equações seguintes,
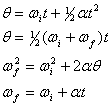
Onde fizemos as substituições, 
Nota que assim como +x é definido arbitrariamente à direita, o valor positivo de theta pode ser definido como no sentido horário ou anti-horário.
- Relação entre variáveis angulares e translacionais
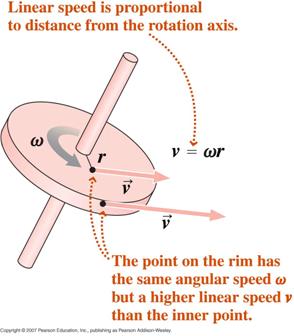Partindo da definição de medida radiana, diferenciando com respeito ao tempo, podemos mostrar que,
onde v é a velocidade tangencial e a é a aceleração tangencial.
>
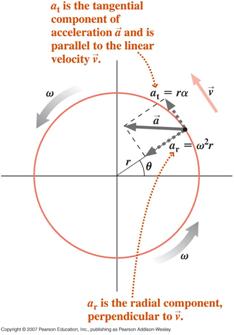
Uma partícula executando movimento circular, com velocidade angular variável (movimento circular não uniforme), experimentará dois componentes de aceleração, um componente tangencial devido à mudança de magnitude de sua velocidade e um componente radial (centrípeta) devido à mudança de direção de sua velocidade
A aceleração líquida da partícula é a soma vetorial destes dois componentes como indicado abaixo.
- Para sua informação…
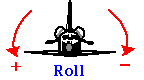
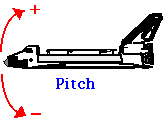
A rotação simultânea de mais de um eixo pode ser considerada de forma semelhante ao movimento projectil, onde estendemos a nossa discussão translacional 1D ao movimento 2D. Em aplicações aeronáuticas, as rotações sobre os três eixos são descritas como Roll, Pitch e Yaw.
Exemplo Problema
“Não quero alcançar a imortalidade através do meu trabalho…Quero alcançá-lo não morrendo”
Woody Allen – Woody Allen and his Comedy (1975)
Dr. C. L. Davis
Departamento de Física
Universidade de Louisville
email: [email protected]
>
