Como Pensar com Exponentes e Logaritmos

Aqui está um truque para pensar em problemas envolvendo exponentes e logs. Basta fazer duas perguntas:

1) Estamos falando de entradas (causa da mudança) ou saídas (a mudança real que aconteceu?)

Logaritmos revelam as entradas que causaram o crescimento
Exponentes encontram o resultado final do crescimento

2) Estamos falando da perspectiva do cultivador, ou de um observador?

e e o log natural são da perspectiva do cultivador instantâneo-a-instantâneo
Base 10, Base 2, etc. são medidas convenientes para um observador humano

Na minha cabeça, coloquei as opções numa tabela:

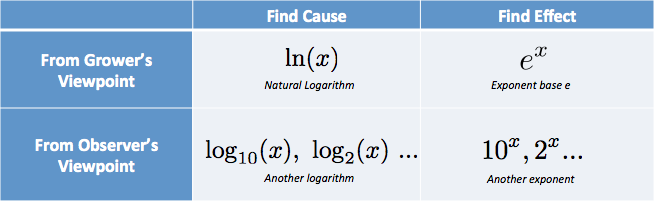comparação do ponto de vista logarítmico exponente >

Eu tenho pensamentos como “Eu preciso da causa, da perspectiva do cultivador… esse é o log natural”. (Log natural é abreviado com LN em minúsculas, a partir do logaritmo alto-falutin’ naturalis.)

Estava frustrado com as classes que descreviam a parte interna da tabela, as funções brutas, sem as legendas que explicavam quando usá-las!

Isso não vai voar, vamos praticar o pensamento direto com logs e expoentes.

Cenário: Descrevendo o Crescimento do PIB

Aqui está um exemplo típico de crescimento:

De 2000 a 2010, o PIB dos EUA mudou de 9,9 trilhões para 14,4 trilhões

Ok, claro, esses números mostram que a mudança aconteceu. Mas nós provavelmente queremos ter uma visão da causa: Que taxa média de crescimento anual seria responsável por esta mudança?

Imediatamente, o meu cérebro pensa em “logaritmos” porque estamos a trabalhar para trás desde o crescimento até à taxa que o causou. \texto (causa do crescimento) }

Um bom começo, mas vamos afiá-lo.

Primeiro, qual logaritmo devemos usar?

Por defeito, eu escolho o logaritmo natural. A maioria dos eventos acaba sendo em termos do cultivador (não observador), e eu gosto de “cavalgar junto” com o elemento de crescimento para visualizar o que está acontecendo. (Os radianos são semelhantes: eles medem ângulos em termos do movedor.)

Próxima pergunta: que mudança aplicamos o logaritmo para?

Estamos realmente interessados na relação entre o início e o fim: 9,9 trilhões para 14,4 trilhões em 10 anos. Esta é a mesma taxa de crescimento que vai de \$9,90 a \$14,40 no mesmo período.

Podemos aguçar o nosso pensamento:

>9752>\displaystyle{\i1}text (logaritmo natural da taxa de crescimento) \texto (causa do crescimento) 4228>

Ok, a causa foi uma taxa de 0,374 ou 37,4%. Já terminámos?

Not ainda. Os logaritmos não sabem quanto tempo demorou uma mudança (não ligamos em 10 anos, certo?). Eles nos dão uma taxa como se toda a mudança tivesse ocorrido em um único período de tempo.

A mudança poderia realmente ser um único ano de 37,4% de crescimento contínuo, ou 2 anos de 18,7% de crescimento, ou alguma outra combinação.

Do cenário, sabemos que a mudança levou 10 anos, então a taxa deve ter sido:

$\displaystyle{ \text{rate} = \frac{.374}{10} = .0374 = 3.74\%}$

Do ponto de vista do crescimento instantâneo e contínuo, a economia americana cresceu 3.74% ao ano.

Agora estamos prontos? Não exactamente!

Esta taxa contínua é da perspectiva do cultivador, como se estivéssemos a “cavalgar” com a economia à medida que ela muda. Um banqueiro provavelmente se preocupa com a diferença de um ano para o outro. Podemos descobrir isso deixando o crescimento contínuo correr durante um ano:

\displaystyle{\i}text{\i1}exponente com taxa e tempo \texto (efeito do crescimento) }

\displaystyle{e^{\text{rate} Aqui está outra maneira de colocar:

De uma base instantânea por instante, uma determinada parte da economia está crescendo em 3,74%, modelada por $e^(.0374 * anos)$
Em uma base anual, com efeitos compostos trabalhados, a economia cresce 3,81%, modelada por $1,0381^anos$

Em finanças, podemos querer a mudança de ano para ano, que pode ser comparada com outras tendências. Em ciência e engenharia, preferimos o comportamento de modelagem instantânea.

Scenario: Descrevendo Crescimento Natural

Detesto exemplos como “Assumir que as bactérias dobram a cada 24 horas, encontrar a sua fórmula de crescimento”. As colônias de bactérias se replicam em intervalos humanos limpos, e esperamos por uma duplicação exata?

Um cenário melhor: “Ei, eu encontrei algumas bactérias, esperei uma hora, e o caroço cresceu de 2,3 gramas para 2,32 gramas. Eu vou almoçar agora. Descubra quanto teremos quando eu voltar em 3 horas”

Vejamos o modelo deste. Vamos precisar de um logaritmo para encontrar a taxa de crescimento, e depois um expoente para projectar esse crescimento para a frente. Como antes, vamos manter tudo em termos do log natural para começar.

O fator de crescimento é:

\displaystyle{\i}text{logaritmo de mudança} \texto (causa do crescimento) }

$\i>estilo de exibição{\i} = \i(2.32/2.3) = .0086 = .86\%}$

Esta é a taxa para uma hora, e o modelo geral para projetar para frente será

\i>estilo de exibição{\i}{\i1}estilo de exibição{\i}exponente com taxa e tempo \texto (efeito do crescimento) 3136

Apenas por diversão, quanto tempo até as bactérias dobrarem? Imagine esperar 1 para virar para 2:

$>9085>\i1 ^{.0086 ^{.0086 {.0086 ^cdot ^text{horas}} = 2}$

Podemos mecanicamente tomar o log natural de ambos os lados para “desfazer o expoente”, mas vamos pensar intuitivamente.

Se 2 é o resultado final, então ln(2) é o input de crescimento que nos levou até lá (alguma taxa × tempo). Sabemos que a taxa foi .0086, então o tempo para chegar a 2 seria:

$\displaystyle{ \i1}{\i1}{\i1}frac{\i(2)}{\i1}{\i1} = \i1}frac{.693}{.0086} = 80.58}$

A colónia irá duplicar após ~80 horas. (Ainda bem que não ficou por aqui?)

O que significa realmente a mudança de perspectiva?

Perguntar se quer a entrada (causa do crescimento) ou a saída (resultado do crescimento) é bastante simples. Mas como você visualiza a perspectiva do cultivador?

Imagine que temos pequenos trabalhadores que estão construindo o padrão de crescimento final (veja o artigo sobre expoentes):

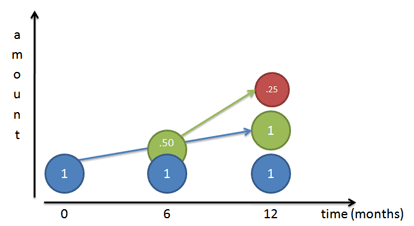
$juros compostos$

Se nossa taxa de crescimento for 100%, estamos dizendo ao nosso trabalhador inicial (Mr. Blue) para trabalhar de forma constante e criar uma cópia de 100% de si mesmo até o final do ano. Se o seguirmos dia a dia, vemos que ele termina uma cópia de 100% de si mesmo (Sr. Green) no final do ano.

Mas… aquele trabalhador que ele estava construindo (Sr. Green) começa a trabalhar também. Se o Sr. Green aparece pela primeira vez na marca dos 6 meses, ele tem um semestre para trabalhar (mesma taxa anual do Sr. Blue) e ele constrói o Sr. Red. É claro, o Sr. Red acaba sendo metade, já que o Sr. Green só tem 6 meses.

E se o Sr. Green aparecesse depois de 4 meses? Um mês? Um dia? Um segundo? Se os trabalhadores começam a crescer imediatamente, obtemos a curva instantâneo-por-instantâneo definida por $e^x$:

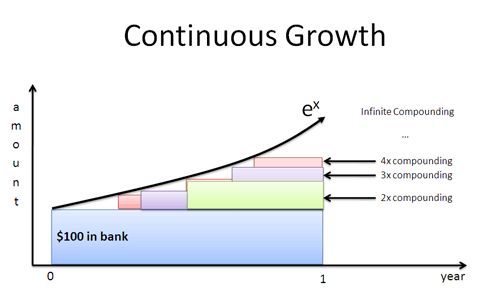
crescimento contínuo

O tronco natural dá uma taxa de crescimento em termos da perspectiva de um trabalhador individual. Nós ligamos essa taxa em $e^x$ para encontrar o resultado final, com todos os compostos incluídos.

Usando Outras Bases

Comutação para outro tipo de logaritmo (base 10, base 2, etc.) significa que estamos procurando por algum padrão no crescimento geral, não o que o trabalhador individual está fazendo.

Cada logaritmo faz uma pergunta ao ver uma mudança:

Log base e: Qual foi a taxa instantânea seguida por cada trabalhador?
Base de registo 2: Quantas duplicações foram necessárias?
Base de registo 10: Quantas duplicações 10x foram necessárias?

Aqui está um cenário a analisar:

Acima de 30 anos, o transistor conta com chips típicos passou de 1000 para 1 bilhão

Como você analisaria isso?

Microchips não são uma entidade única que cresce suavemente com o tempo. São edições separadas, de empresas concorrentes, e indicam uma tendência tecnológica geral.
Desde que não estamos “cavalgando junto” com um microchip em expansão, vamos usar uma escala feita para conveniência humana. Dobrar é mais fácil de pensar do que 10x-ing.

Com estas suposições obtemos:

\displaystyle{\i}text{logaritmo da mudança} \texto (causa do crescimento) }

Displaystyle{\i1}{\i1000} = {\i1}log_2({\i1000}) {\i1}(\i1 milhão) {\i1}sim {\i1}4684>

A “causa do crescimento” foi 20 duplicações, que sabemos que ocorreram ao longo de 30 anos. Esta média é de 2/3 duplicações por ano, ou 1,5 anos por duplicação – uma boa regra de ouro.

Da perspectiva do cultivador, computaríamos $\ln(\text{1 bilhão}/1000) / \text{30 anos} = 46\%$ crescimento contínuo (um pouco mais difícil de relacionar neste cenário).

Podemos resumir nossa análise em uma tabela:

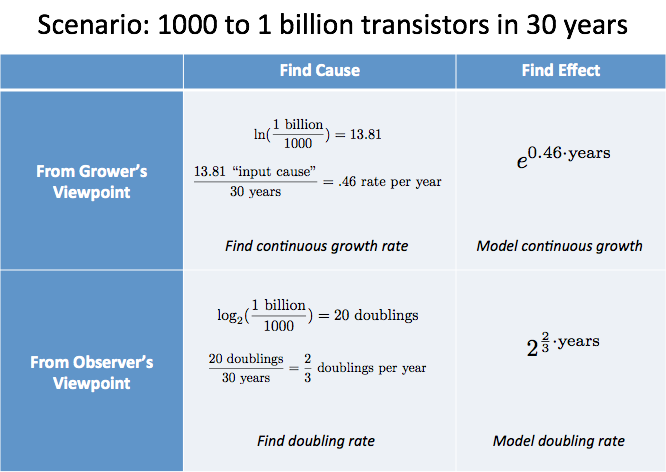
exemplo de transistorexponente

Sumário

Aprender é encontrar as legendas ocultas por trás de um conceito. Quando é usado? Que ponto de vista ele traz ao problema?

A minha interpretação atual é que os expoentes perguntam sobre causa vs. efeito e cultivador vs. observador. Mas nós nunca terminamos; parte da diversão é ver como podemos recapturar conceitos antigos.

Feliz matemática.

Anexo: A Fórmula da Mudança de Base

Aqui está como pensar em mudar de base. Assumindo uma taxa de crescimento 100% contínua,

ln(x) é o tempo para crescer até x
ln(2) é o tempo para crescer até 2

Desde que temos tempo para duplicar, podemos ver quantos “caberiam” no tempo total para crescer até x:

$>>92>></p>><p>Por exemplo, quantas dobras ocorrem de 1 a x} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

Por exemplo, quantas dobras ocorrem de 1 a 64?

Well, ln(64) = 4,158. E ln(2) = .693. O número de dobras que cabem é:

$\displaystyle{\frac{\ln(64)}{\ln(2)} = \frac{4.158}{.693} = 6}$

No mundo real, as calculadoras podem perder precisão, então use uma função de log base 2 direta, se possível. E, claro, podemos ter um número fracionário: Passar de 1 para a raiz quadrada de 2 é “metade” uma duplicação, ou log2(1.414) = 0.5.

Mudando para log base 10 significa que estamos a contar o número de 10x-ings que cabem:

$\displaystyle{\text{\i}{\i1}número de 10x-ings de 1 a x} = \frac{\i(x)}{\i(x)} = \log_{\i(10}(x) }$

Neat, certo? Leia Usando Logaritmos no Mundo Real para mais exemplos.

Outros Posts Nesta Série

Um Guia Intuitivo para Funções Exponenciais & e
Demistificar o Logaritmo Natural (ln)
Um Guia Visual para Taxas de Interesse Simples, Composto e Contínuo
Definições Comuns de e (Colorido)
Expoentes Compreensíveis (Porque é que 0^0 = 1?)
Usando Logaritmos no Mundo Real
Como pensar com expoentes e logaritmos
Entendendo Crescimento discreto vs. contínuo
O que realmente significa um expoente?
Q: Por que é e especial? (2.718…, não 2, 3.7 ou outro número?)