Less…
![]()
Existem muitas fórmulas de ![]() de muitos tipos. Entre outras, estas incluem séries, produtos, construções geométricas, limites, valores especiais e iterações pi.
de muitos tipos. Entre outras, estas incluem séries, produtos, construções geométricas, limites, valores especiais e iterações pi.
![]() está intimamente relacionado com as propriedades dos círculos e esferas. Para um círculo de raio
está intimamente relacionado com as propriedades dos círculos e esferas. Para um círculo de raio ![]() , a circunferência e a área são dadas por
, a circunferência e a área são dadas por
|
(1)
|
|||
|
(2)
|
Similiarmente, para uma esfera de raio ![]() , a área de superfície e o volume delimitado são
, a área de superfície e o volume delimitado são
|
(3)
|
|||
|
(4)
|
Uma fórmula exata para ![]() em termos das tangentes inversas das frações unitárias é a fórmula de Machin
em termos das tangentes inversas das frações unitárias é a fórmula de Machin
|
(5)
|
Existem três outras fórmulas semelhantes à máquina, bem como milhares de outras fórmulas semelhantes com mais termos.
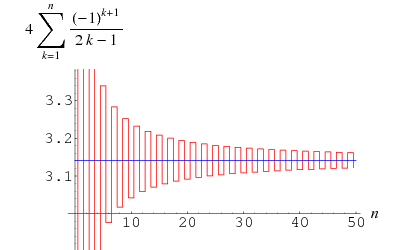
Gregory e Leibniz encontrados
|
(6)
|
|||
|
(7)
|
(Wells 1986, p. 50), que é conhecido como a série Gregory e pode ser obtido ligando ![]() à série Leibniz para
à série Leibniz para ![]() . O erro após o termo
. O erro após o termo ![]() desta série na série Gregory é maior que
desta série na série Gregory é maior que ![]() pelo que esta soma converge tão lentamente que 300 termos não são suficientes para calcular
pelo que esta soma converge tão lentamente que 300 termos não são suficientes para calcular ![]() correctamente com duas casas decimais! Entretanto, ela pode ser transformada para
correctamente com duas casas decimais! Entretanto, ela pode ser transformada para
|
(8)
|
where ![]() é a função zeta de Riemann (Vardi 1991, pp. 157-158; Flajolet e Vardi 1996), de modo que o erro após
é a função zeta de Riemann (Vardi 1991, pp. 157-158; Flajolet e Vardi 1996), de modo que o erro após ![]() termos é
termos é ![]() .
.
Uma série de soma infinita para Abraham Sharp (ca. 1717) é dada por
|
(9)
|
(Smith 1953, p. 311). Outras séries simples nas quais ![]() aparece são
aparece são
|
|
(10)
|
||
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
|||
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
(Wells 1986, p. 53).
em 1666, Newton usou uma construção geométrica para derivar a fórmula
|
(18)
|
|||
|
(19)
|
que calculou ![]() (Wells 1986, p. 50; Borwein et al. 1989; Borwein e Bailey 2003, pp. 105-106). Os coeficientes podem ser encontrados a partir da integral
(Wells 1986, p. 50; Borwein et al. 1989; Borwein e Bailey 2003, pp. 105-106). Os coeficientes podem ser encontrados a partir da integral
|
(20)
|
|||
|
(21)
|
tomando a expansão da série de ![]() cerca de 0, obtaining
cerca de 0, obtaining
|
(22)
|
(OEIS A054387 e A054388). Usando a transformação de melhoria da convergência de Euler dá
|
(23)
|
|||
|
(24)
|
|||
|
(25)
|
(Beeler et al. 1972, Item 120).
>
Corresponde à ligação ![]() à série de potências para a função hipergeométrica
à série de potências para a função hipergeométrica ![]() ,
,
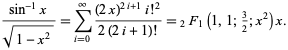 |
(26)
|
Embora a melhoria da convergência, a série (◇) converge em apenas um bit/terminal. Ao custo de uma raiz quadrada, Gosper notou que ![]() dá 2 bits/term,
dá 2 bits/term,
|
(27)
|
e ![]() dá quase 3.39 bits/term,
dá quase 3.39 bits/term,
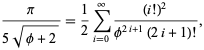
where ![]() é a razão áurea. Gosper também obtido
é a razão áurea. Gosper também obtido
|
(29)
|
Um algoritmo de espigão para ![]() é dado por Rabinowitz e Wagon (1995; Borwein e Bailey 2003, pp. 141-142).
é dado por Rabinowitz e Wagon (1995; Borwein e Bailey 2003, pp. 141-142).
Mais espantosamente imóvel, uma expressão de forma fechada dando um algoritmo de extração de dígitos que produz dígitos de ![]() (ou
(ou ![]() ) na base -16 foi descoberta por Bailey et al. (Bailey et al. 1997, Adamchik e Wagon 1997),
) na base -16 foi descoberta por Bailey et al. (Bailey et al. 1997, Adamchik e Wagon 1997),
|
(30)
|
Esta fórmula, conhecida como a fórmula BBP, foi descoberta usando o algoritmo PSLQ (Ferguson et al. 1999) e é equivalente a
|
(31)
|
Há uma série de fórmulas do tipo BBP para ![]() em poderes de
em poderes de ![]() , as primeiras fórmulas independentes das quais são
, as primeiras fórmulas independentes das quais são
|
(32)
|
|||
|
(33)
|
|||
|
(34)
|
|||
 |
(35)
|
||
 |
(36)
|
||
 |
(37)
|
Simplesmente, há uma série de fórmulas do tipo BBP para ![]() em potências de
em potências de ![]() , as primeiras fórmulas independentes das quais são
, as primeiras fórmulas independentes das quais são
|
(38)
|
|||
|
(39)
|
|||
 |
(40)
|
||
 |
(41)
|
||
 |
(42)
|
||
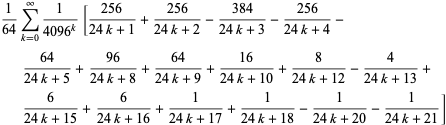 |
(43)
|
||
 |
(44)
|
||
 |
(45)
|
||
|
|
 |
(46)
|
|
 |
(47)
|
||
 |
(48)
|
F. Bellard encontrou a fórmula do tipo BBP de rápida convergência
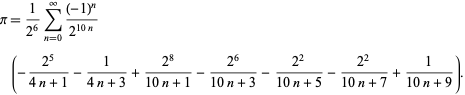 |
(49)
|
Uma integral relacionada é
|
(50)
|
(Dalzell 1944, 1971; Le Lionnais 1983, p. 22; Borwein, Bailey, e Girgensohn 2004, p. 3; Boros e Moll 2004, p. 125; Lucas 2005; Borwein et al. 2007, p. 14). Esta integral foi conhecida por K. Mahler em meados dos anos 60 e aparece em um exame na Universidade de Sydney em novembro de 1960 (Borwein, Bailey, e Girgensohn, p. 3). Beukers (2000) e Boros e Moll (2004, p. 126) afirmam que não está claro se existe uma escolha natural de polinômio racional cuja integral entre 0 e 1 produz ![]() , onde 333/106 é a próxima convergente. Contudo, existe uma integral para a quarta convergente, nomeadamente
, onde 333/106 é a próxima convergente. Contudo, existe uma integral para a quarta convergente, nomeadamente
|
(51)
|
(Lucas 2005; Bailey et al. 2007, p. 219). Na verdade, Lucas (2005) dá poucos outros integrais desse tipo.
Backhouse (1995) usou a identidade
| |
(52)
|
||
|
(53)
|
|||
|
(54)
|
para número inteiro positivo ![]() e
e ![]() e onde
e onde ![]() ,
, ![]() , e
, e ![]() são constantes racionais para gerar um número de fórmulas para
são constantes racionais para gerar um número de fórmulas para ![]() . Em particular, se
. Em particular, se ![]() , então
, então ![]() (Lucas 2005).
(Lucas 2005).
Uma fórmula semelhante foi subsequentemente descoberta por Ferguson, levando a uma malha bidimensional de tais fórmulas que pode ser gerada por estas duas fórmulas dadas por
|
(55)
|
para qualquer valor complexo de ![]() (Adamchik e Wagon), dando a fórmula do BBP como caso especial
(Adamchik e Wagon), dando a fórmula do BBP como caso especial ![]() .
.
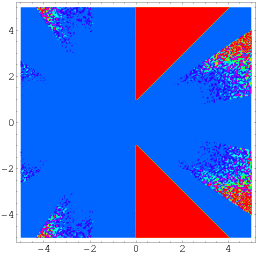
Uma identidade ainda mais geral devido ao Wagon é dada por
 |
(56)
|
(Borwein e Bailey 2003, p. 141), que se mantém sobre uma região do plano complexo excluindo duas porções triangulares simetricamente colocadas sobre o eixo real, como ilustrado acima.
Uma classe geral de identidades talvez ainda mais estranha é dada por
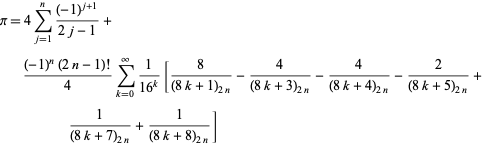 |
(57)
|
que detém para qualquer número inteiro positivo ![]() , onde
, onde ![]() é um símbolo Pochhammer (B. Cloitre, pers. comm, 23 de janeiro de 2005). Ainda mais surpreendente, existe uma fórmula análoga para o logaritmo natural de 2.
é um símbolo Pochhammer (B. Cloitre, pers. comm, 23 de janeiro de 2005). Ainda mais surpreendente, existe uma fórmula análoga para o logaritmo natural de 2.
Na sequência da descoberta da fórmula BBP de 16 dígitos base e fórmulas relacionadas, fórmulas semelhantes em outras bases foram investigadas. Borwein, Bailey e Girgensohn (2004) mostraram recentemente que ![]() não tem fórmula arctangente BBP tipo máquina que não seja binária, embora isto não exclua um esquema completamente diferente para algoritmos de extração de dígitos em outras bases.
não tem fórmula arctangente BBP tipo máquina que não seja binária, embora isto não exclua um esquema completamente diferente para algoritmos de extração de dígitos em outras bases.
S. Plouffe concebeu um algoritmo para calcular o ![]() ésimo dígito de
ésimo dígito de ![]() em qualquer base em
em qualquer base em ![]() passos.
passos.
Uma série de identidades adicionais devidas a Ramanujan, Catalão, e Newton são dadas por Castellanos (1988ab, pp. 86-88), incluindo várias envolvendo somas de números de Fibonacci. Ramanujan encontrou
 |
(58)
|
(Hardy 1923, 1924, 1999, p. 7).
Plouffe (2006) encontrou a bela fórmula
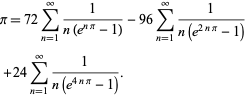 |
(59)
|
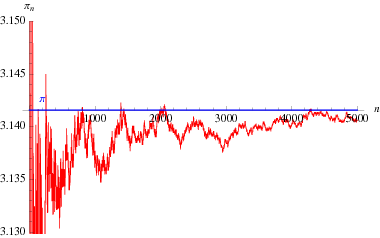
Uma interessante fórmula de produto infinito devido a Euler que relaciona ![]() e o
e o ![]() th prime
th prime ![]() é
é
 |
(60)
|
||
|
(61)
|
(Blatner 1997, p. 119), plotado acima em função do número de termos no produto.
Um método semelhante ao de Arquimedes pode ser usado para estimar ![]() , começando com um
, começando com um ![]() -gon e depois relacionando a área de subseqüentes
-gon e depois relacionando a área de subseqüentes ![]() -gons. Seja
-gons. Seja ![]() o ângulo a partir do centro de um dos segmentos do polígono,
o ângulo a partir do centro de um dos segmentos do polígono,
|
(62)
|
então
|
(63)
|
(Beckmann 1989, pp. 92-94).
Vieta (1593) foi o primeiro a dar uma expressão exata para ![]() tomando
tomando ![]() na expressão acima, dando
na expressão acima, dando
|
(64)
|
que leva a um produto infinito de nestedradicals,
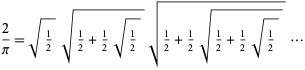 |
(65)
|
(Wells 1986, p. 50; Beckmann 1989, p. 95). Entretanto, esta expressão não foi rigorosamente provada para convergir até Rudio em 1892.
Uma fórmula relacionada é dada por
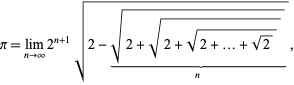 |
(66)
|
que pode ser escrito
|
(67)
|
>
onde ![]() é definido usando a iteração
é definido usando a iteração
 |
(68)
|
with ![]() (J. Munkhammar, pers. comm.., 27 de Abril de 2000). A fórmula
(J. Munkhammar, pers. comm.., 27 de Abril de 2000). A fórmula
 |
(69)
|
também está intimamente relacionado.
Uma fórmula bonita para ![]() é dada por
é dada por
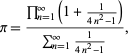 |
(70)
|
Onde o numerador é uma forma da fórmula Wallis para ![]() e o denominador é uma soma telescópica com soma 1/2 desde
e o denominador é uma soma telescópica com soma 1/2 desde
|
(71)
|
(Sondow 1997).
Um caso particular da fórmula Wallis dá
|
(72)
|
(Wells 1986, p. 50). Esta fórmula também pode ser escrita
 |
(73)
|
where ![]() denota um coeficiente binomial e
denota um coeficiente binomial e ![]() é a função gama (Knopp 1990). Euler obtido
é a função gama (Knopp 1990). Euler obtido
|
(74)
|
que decorre do valor especial da função zeta de Riemann ![]() . Fórmulas similares seguem de
. Fórmulas similares seguem de ![]() para todos os inteiros positivos
para todos os inteiros positivos ![]() .
.
Uma soma infinita devida a Ramanujan é
|
(75)
|
(Borwein et al. 1989; Borwein e Bailey 2003, p. 109; Bailey et al.2007, p. 44). Outras somas são dadas em Ramanujan (1913-14),
e
|
(77)
|
|||
|
(78)
|
(Beeler et al. 1972, Item 139; Borwein et al. 1989; Borwein and Bailey 2003, p. 108; Bailey et al. 2007, p. 44). A equação (78) é derivada de uma identidade modular de ordem 58, embora uma primeira derivação não tenha sido apresentada antes de Borwein e Borwein (1987). As séries acima dão ambas
|
(79)
|
(Wells 1986, p. 54) como primeira aproximação e fornecer, respectivamente, cerca de 6 e 8 casas decimais por termo. Tais séries existem devido à racionalidade de várias invariantes modulares.
A forma geral da série é
|
(80)
|
onde ![]() é uma forma quadrática binária discriminante,
é uma forma quadrática binária discriminante, ![]() é a função j,
é a função j,
|
(81)
|
|||
|
(82)
|
e os ![]() são séries Eisenstein. Um número de classe
são séries Eisenstein. Um número de classe ![]() campo envolve
campo envolve ![]() inteiros algébricos de grau das constantes
inteiros algébricos de grau das constantes ![]() ,
, ![]() , e
, e ![]() . De todas as séries que consistem de apenas termos inteiros, a que dá os dígitos mais numéricos no menor período de tempo corresponde à maior discriminação de classe número 1 de
. De todas as séries que consistem de apenas termos inteiros, a que dá os dígitos mais numéricos no menor período de tempo corresponde à maior discriminação de classe número 1 de ![]() e foi formulada pelos irmãos Chudnovsky (1987). O 163 que aparece aqui é o mesmo que aparece no fato de
e foi formulada pelos irmãos Chudnovsky (1987). O 163 que aparece aqui é o mesmo que aparece no fato de ![]() (a constante Ramanujan) ser muito próximo de um inteiro. Da mesma forma, o fator
(a constante Ramanujan) ser muito próximo de um inteiro. Da mesma forma, o fator ![]() vem da identidade da função j para
vem da identidade da função j para ![]() . A série é dada por
. A série é dada por
|
(83)
|
|||
| >
(84)
|
(Borwein e Borwein 1993; Beck e Trott; Bailey et al. 2007, p. 44). Esta série dá 14 dígitos com precisão por termo. A mesma equação em outra forma foi dada pelos irmãos Chudnovsky (1987) e é usada pela linguagem Wolfram para calcular ![]() (Vardi 1991; Wolfram Research),
(Vardi 1991; Wolfram Research),
|
(85)
|
where
|
(86)
|
|||
|
(87)
|
|||
|
(88)
|
A melhor fórmula para a classe número 2 (maior discriminante ![]() ) é
) é
|
(89)
|
where
|
(90)
|
|||
|
(91)
|
|||
|
(92)
|
(Borwein e Borwein 1993). Esta série acrescenta cerca de 25 dígitos para cada termo adicional. A série convergente mais rápida para a classe número 3 corresponde a ![]() e dá 37-38 dígitos por termo. A série mais rápida da classe convergente número 4 corresponde a
e dá 37-38 dígitos por termo. A série mais rápida da classe convergente número 4 corresponde a ![]() e é
e é
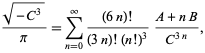 |
(93)
|
where
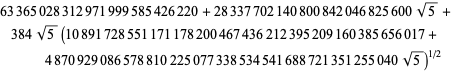 |
(94)
|
||
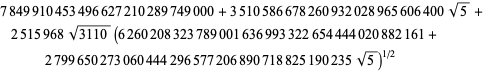 |
(95)
|
||
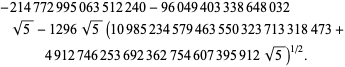 |
(96)
|
Põe 50 dígitos por termo. Borwein e Borwein (1993) desenvolveram um algoritmo geral para gerar tais séries para número de classe arbitrária.
Uma lista completa das séries da Ramanujan para ![]() encontradas em seus segundo e terceiro cadernos é dada por Berndt (1994, pp. 352-354),
encontradas em seus segundo e terceiro cadernos é dada por Berndt (1994, pp. 352-354),
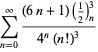 |
(97)
|
||
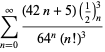 |
(98)
|
||
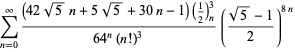 |
(99)
|
||
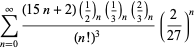 |
(100)
|
||
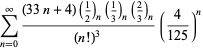 |
(101)
|
||
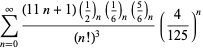 |
(102)
|
||
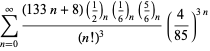 |
(103)
|
||
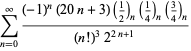 |
(104)
|
||
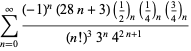 |
(105)
|
||
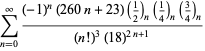 |
(106)
|
||
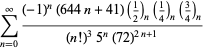 |
(107)
|
||
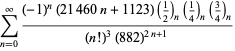 |
(108)
|
||
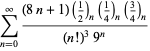 |
(109)
|
||
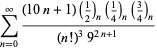 |
(110)
|
||
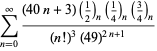 |
(111)
|
||
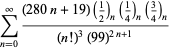 |
(112)
|
||
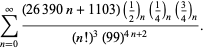 |
(113)
|
Estas equações foram provadas pela primeira vez por Borwein e Borwein (1987a, pp. 177-187). Borwein e Borwein (1987b, 1988, 1993) provaram outras equações deste tipo, e Chudnovsky e Chudnovsky (1987) encontraram equações semelhantes para outras constantes transcendentais (Bailey et al. 2007, pp. 44-45).
Uma lista completa de equações independentes conhecidas deste tipo é dada por
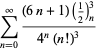 |
(114)
|
||
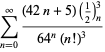 |
(115)
|
||
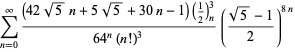 |
(116)
|
||
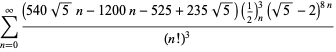 |
(117)
|
||
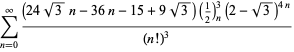 |
(118)
|
para ![]() com sinais não permanentes,
com sinais não permanentes,
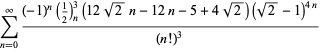 |
(119)
|
||
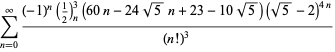 |
(120)
|
||
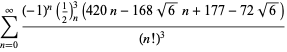 |
(121)
|
||
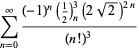 |
(122)
|
para ![]() com sinais alternados,
com sinais alternados,
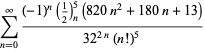 |
(123)
|
||
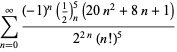 |
(124)
|
para ![]() (Guillera 2002, 2003, 2006),
(Guillera 2002, 2003, 2006),
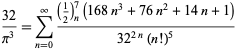 |
(125)
|
para ![]() (Guillera 2002, 2003, 2006), e nenhum outro para
(Guillera 2002, 2003, 2006), e nenhum outro para ![]() são conhecidos (Bailey et al. 2007, pp. 45-48).
são conhecidos (Bailey et al. 2007, pp. 45-48).
Bellard dá a fórmula exótica
 |
(126)
|
where
|
(127)
|
Gasper cita o resultado
|
(128)
|
where ![]() é uma função hipergeométrica generalizada, e transforma-a em
é uma função hipergeométrica generalizada, e transforma-a em
Um resultado fascinante devido a Gosper é dado por
|
(130)
|
![]() satisfaz a desigualdade
satisfaz a desigualdade
|
(131)
|
D. Terr (pers. comm.) notou a curiosa identidade
|
(132)
|
envolvendo os primeiros 9 dígitos de pi.