Proporcional é apenas uma forma de reagir a um erro no sistema. O problema com o controle proporcional é que ele não consegue detectar tendências e se ajustar a elas. Este é o trabalho do controle integral.
Existe outro exemplo de gráfico do erro em um sistema ao longo do tempo, à esquerda da Figura 6. Novamente, pode ser a distância de um robô de um objeto, ou pode ser o nível de fluido em um tanque, ou a temperatura em um forno de fábrica. Talvez o alvo que o robô está seguindo continue se afastando do robô a uma velocidade que o robô não está alcançando. Talvez a vedação da porta do forno esteja desgastada; talvez o escoamento do fluido do tanque seja invulgarmente grande. Independentemente da causa, uma vez que o proporcional não é projetado para reagir às tendências, não consegue detectar e corrigir o problema. É aí que entra o controle integral.
Integral mede a área entre os valores de erro e o eixo temporal. Se o erro não voltar a zero, a área do erro torna-se cada vez maior. O lado direito da Figura 6 mostra como a saída integral pode reagir a este tipo de tendência. medida que a área entre a curva de erro e o eixo temporal aumenta, a saída aumenta proporcionalmente a esta área. Como resultado, a saída conduz o atuador com mais força e dificuldade para corrigir o erro.
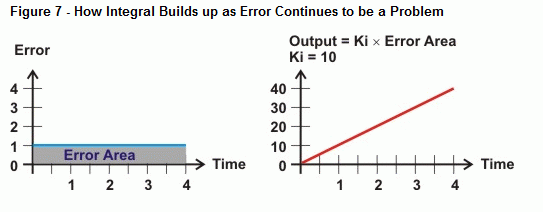
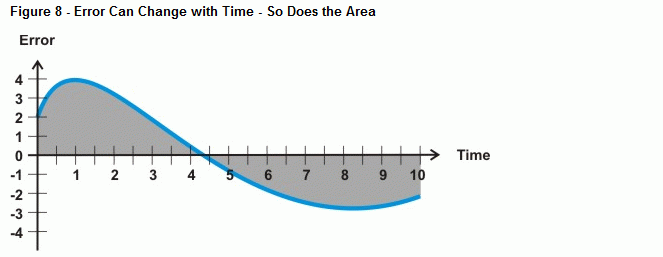
Então o que acontece quando o erro não é uma linha reta, como a curva mostrada na Figura 8? É isso que a operação de cálculo da integração determina, a área entre uma curva e um eixo. No caso de controle integral, à medida que mais tempo passa com um erro, a área sob a curva cresce, assim como o valor que o cálculo integral usará para acionar contra o erro do sistema. Se a curva de erro cai abaixo do eixo temporal, o acúmulo de área negativa subtrai do acúmulo de área positiva. Quando ajustado correctamente, o controlo integral pode ajudar o sistema a afiar um erro de zero.
O carimbo BASIC pode aproximar o erro sob a curva com integração numérica. A Figura 9 mostra como se pode aproximar o erro sob uma curva somando a área de um monte de pequenos rectângulos entre a curva de erro e o eixo temporal. A área de cada caixa é o erro multiplicado pelo tempo entre as medições. Ao somar todas as áreas da caixa, você obtém uma aproximação da área sob a curva.
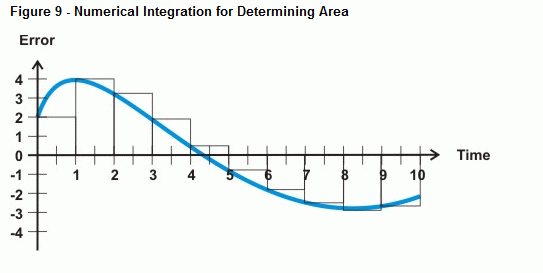
Desde que suas medições estejam uniformemente espaçadas, você pode chamar a largura de cada caixa um valor de 1. Isso torna a matemática muito mais simples do que tentar contabilizar 20 ms entre amostras, 5 minutos entre amostras, ou o que quer que sua taxa de amostragem se torne. Em vez de multiplicar o erro pelo incremento de tempo entre amostras e depois adicionar ao próximo erro multiplicado pelo tempo, basta multiplicar cada amostra de erro por um tempo de 1. O resultado é que você pode simplesmente manter um total de medições de erro em execução para o seu cálculo integral. Aqui está um exemplo de como fazer isso com PBASIC:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
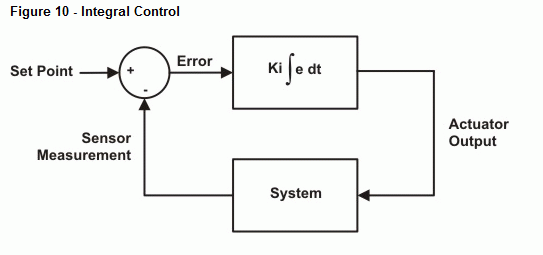
O próximo exemplo de programa executa a integração numérica no sinal de erro e ajusta a saída de acordo. Tal como no controlo proporcional, existe uma constante que dimensiona a saída da integração para o valor desejado. Para simplificar, vamos usar novamente 10 para Ki. A Figura 10 mostra um diagrama de blocos do laço de controle. O termo Kp ∫ edt refere-se a Kp multiplicado pela integral do erro ao longo do tempo. Em outras palavras, Kp multiplicado pela área acumulada entre a curva de erro e o eixo temporal.
Example Program – IntegralAlgorithm.bs2
- Enter, salvar e executar IntegralAlgorithm.bs2.
- Entrar esta sequência de valores na janela de transmissão do terminal de depuração: 3 3 3 3 3 3 3 3 3. Observe como a saída integral fica maior a cada vez que o 3 é repetido. Essa é a tarefa da integral, detectar tendências e aumentar a unidade para corrigi-la conforme necessário.
- Agora tente esta sequência: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. A área sob esta curva é 0 uma vez que a área negativa é a mesma que a área positiva. Isso também é o que o cálculo integral chegará quando você tiver terminado de inserir a seqüência.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Como funciona o IntegralAlgorithm.bs2
Este programa é um programa ProportionalAlgorithm.bs2 modificado para realizar o cálculo integral em seu lugar. Agora há dois tipos diferentes de erros a serem seguidos, então ali a matriz de variáveis de erro foi expandida para dois elementos. A variável error(0) rastreia o erro atual, e error(1) rastreia o erro acumulado. As constantes Current CON 0 e Accumulator CON 1 tornam a contabilidade um pouco mais sensível com error(current) e error(accumulator).
A outra alteração que foi feita é que o erro é acumulado e a saída integral é calculada com estas duas afirmações:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Your Turn – Clamping the Integral Output
Como você pode ter se reunido ao entrar repetidamente 3 no terminal de depuração, a saída do conversor integral pode realmente começar a fugir. Você pode usar os operadores MIN e MAX para evitar que o controle integral seja exagerado com a saída. Vamos repetir a actividade de desvio do servo e limitar a saída de 650 para 850.
- Alterar o conversor = i comando para conversor = i + Desvio MIN 650 MAX 850.
- Executar o programa e verificar se a saída integral está limitada a valores entre 650 e 850. Tente inserir 2 repetidamente, depois -2 repetidamente.