Para a revista académica, ver Tetrahedron (revista).
| Tetraedro regular | |
|---|---|
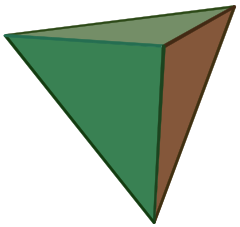 (Clique aqui para modelo rotativo) |
|
| Type | Sólido platónico |
| Elementos | F = 4, E = 6 V = 4 (χ = 2) |
| Faces por lados | 4{3} |
| Schläfli símbolo | {3,3} e s{2,2} |
| Símbolo Wythoff | 3 | 2 3 | 2 2 2 |
| Coxeter-Dynkin | |
| Simetria | Td ou (*332) |
| U01, C15, W1 | |
| Propriedades | Deltahedron convexo regular |
| Ângulo diedro | 70.528779° = arccos(1/3) |
 3.3.3 3.3.3(Figura do vértice) |
 Self-dual (poliedro duplo) |
 Net |
|
Um tetraedro (plural: tetraedro) é um poliedro composto por quatro faces triangulares, três das quais se encontram em cada vértice. Um tetraedro regular é aquele em que os quatro triângulos são regulares, ou “equilátero”, e é um dos sólidos platônicos.
O tetraedro é um tipo de pirâmide, que é um poliedro com uma base poligonal plana e faces triangulares ligando a base a um ponto comum. No caso de um tetraedro a base é um triângulo (qualquer uma das quatro faces pode ser considerada a base), portanto um tetraedro também é conhecido como pirâmide triangular ou Deltahedron Digonal.Commonscat
- F. M. Jackson e Weisstein, Eric W., “Tetrahedron” da MathWorld.
- Weisstein, Eric W., “Tetraedro” da MathWorld.
- Weisstein, Eric W., “Tetraedro” da MathWorld.
- O Poliedro Uniforme
- Tetraedro: Modelo Poliedro Interactivo
- K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Fórmula de Piero della Francesca para o volume de tetraedro em MathPages
- Modelos de papel livres de um tetraedro e muitos outros poliedros
- Um Incrível, Space Filling, Tetraedro não regular que também inclui uma descrição de um “anel rotativo de tetraedro”, também conhecido como um caleidociclo.
- Fórmulas explícitas para o tensor de inércia de um tetraedro arbitrário em termos das suas coordenadas de vértice
- O tensor de inércia de um tetraedro