Transformações Coordenadas

Introdução

Transformações Coordenadas são não suficientemente intuitivas em 2-D, epositivamente dolorosas em 3-D. Esta página aborda-as na seguinte ordem: (i) vectores em 2-D, (ii) tensores em 2-D, (iii) vectores em 3-D, (iv) tensores em 3-D, e finalmente(v) transformadas em tensores de 4ª ordem.
Um aspecto importante das transformações de coordenadas é a avaliação da matriz de transformação, especialmente em 3-D. Isto é abordado aqui, e discutido em detalhe na próxima página.
É muito importante reconhecer que todas as transformações de coordenadas nesta página são rotação do sistema de coordenadas enquanto o próprio objeto permanece fixo. O “objeto” pode ser um vetor, como força ou velocidade, ou um tensor, como tensão ou deformação em um componente. As rotações de objectos são discutidas em secções posteriores.

2-D Transformações de Coordenadas de Vectores

A batata académica fornece um excelente exemplo de como as transformações de coordenadas se aplicam aos vectores, ao mesmo tempo que sublinha que é o sistema de coordenadas que está a rodar e não o vector… ou a batata.
A batata à esquerda tem um vector. Mas sem um sistema de coordenadas, não há forma de descrever o vector. Assim, um sistema de coordenadas foi adicionado à batata como mostrado à direita, permitindo que o vector seja agora descrito como {\bf v} = 2{\bf i} + 9{\bf j}).

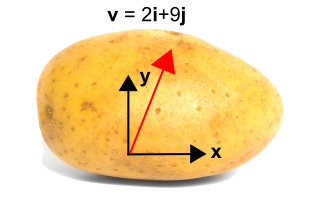
Então agora introduzimos um sistema de coordenadas rodadas mostrado em azul abaixo, usando {{\i} e {\i}(x’}). O novo sistema é rodado no sentido contrário ao dos ponteiros do relógio por um ângulo, a partir do sistema de coordenadas inicial. Note que o vetor não se altera em nada. Continua a ser o mesmo vector que antes. Mas é descrito por diferentes valores numéricos no novo sistema de coordenadas. Neste caso, o vector está mais próximo do novo eixo do que do eixo y, portanto o componente será maior do que o componente j’j. A transformação é dada abaixo da figura.
As equações de transformação vectoriais 2-D são

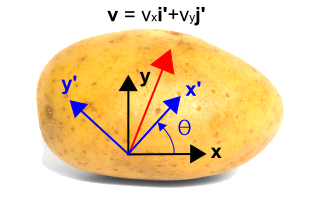
Isto pode ser visto observando que estes quatro factores compõem os quatro termos nas equações de transformação. Eles são facilmente verificados ajustando {theta = 0 ^circ ^) e {theta = 90 ^circ ^). Quando se define 0 {theta = 0 ^circ}, depois v’_x = v_x} e v’_y = v_y}. Quando… quando… quando… quando… quando… quando…

Matriz de Transformação

É mais conveniente escrever (e trabalhar com) equações de transformação usando matrizes.
>esquerda{v_x v_y} \Os termos estão na diagonal da matriz, enquanto os termos em diagonal estão fora da diagonal. O único potencial que se tem é lembrar qual termo tem o sinal de menos. É sempre o termo inferior esquerdo.

A equação acima está escrita na notação da matriz como

onde {\bf Q}} é a letra usual escolhida para a matriz de transformação.

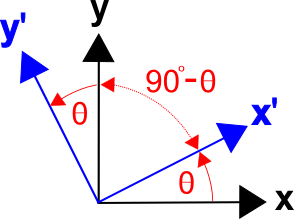
Existe um método geral para formular matrizes de transformação baseadas nos cossines dos ângulos entre os eixos dos dois sistemas de coordenadas, ou seja, cossines de direção. A matriz de transformação pode ser escrita como

onde \((x’,x)\) representa o ângulo entre os eixos \(x’\) e \(x),\((x’,y)\) é o ângulo entre os eixos \(x’\) e \(y)\), etc.
O ângulo entre os eixos é((90^^circ -theta)|, e {\an8}(x’,y} = {\an8}cos(x’,y) = {\an8}cos(90^^circ -theta)|sintheta){\an8}
Likewise, o ângulo entre y'{\i} e x'{\i} é((90^^circ + {\i}theta){\i}, e {\i(y’,x} = {\i(90^circ + {\i}theta) = -sin-theta).

Notação do sensor

A transformação coordenada é escrita em notação tensorial como

>onde {\i}(lambda_{ij}) é a matriz de transformação. (Não sei porque é que o Q é usado na notação matricial, mas o Lambda, não o Q, é usado na notação tensorial). \Por exemplo, se lambda_{ij}} é definido como
Por exemplo, se lambda_(i = 1}) e {j = 2}, então
(lambda_{ij}) é a direção cosseno do ângulo entre o eixo {x’_i} e o eixo {x_j}. Novamente, isto é igualmente aplicável às transformações 3D também.

2-D Transformações de tensores de coordenadas

Esta seção apresentará o que e como das transformações de tensores. O porquê terá que esperar até mais tarde.
Transformações de coordenadas de tensores de 2º grau envolvem a mesma matriz que as transformações vetoriais. Uma transformação do tensor de tensão, o símbolo de fobras, do sistema de coordenadas de referência para o símbolo de fobras, num novo sistema, é feita da seguinte forma.

Escrever as matrizes explicitamente dá
=esquerda
(Note que o tensor de tensão é sempre simétrico, mesmo após transformações.)
Multiplicando as matrizes para fora dá

Estas três equações são exatamente a transformação 2-D de um tensor de tensão resultante de forças de amortecimento sobre um elemento diferencial e impondo equilíbrio. Isto também é representado pelo círculo de Mohr.

Notação tensora

A transformação coordenada é escrita em notação tensora como

Como de costume, a notação tensora fornece uma visão extra do processo. Desta vez, o insight vem dos subscritos nos lambdas. Cada lambda efetivamente emparelha um subescrito no símbolo do tensor com um no símbolo do tensor, independentemente da classificação do tensor.

3-D Transformações de Coordenadas de Vectores

Muitas das equações gerais usadas nas transformações 2D são também aplicáveis nas transformações 3D. Os vectores têm componentes z e os transformadores são 3×3 em vez de 2×2,
6855
6855
6 esquerda{ v_x v_y v_z } \direita]

3-D Transformações de Coordenadas de Tensores

Apenas as regras não mudam, apenas os detalhes mudam.

Escrever as matrizes dá explicitamente
>

Esta página web realiza transformações de coordenadas em tensores 3-D. Experimente.

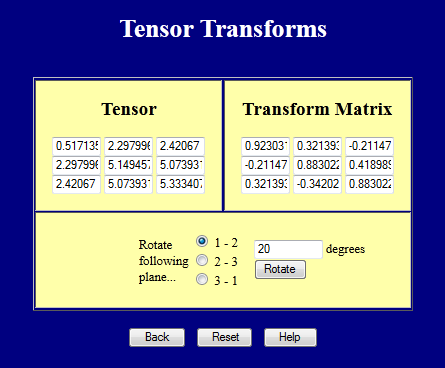
Transformações Coordenadas de Tensores de 4ª Classe

Vemos na seção sobre a Lei de Hooke que o tensor de rigidez é de 4ª classe, ou seja, 3x3x3x3 (não 4×4). Está escrito como C_ijkl porque relaciona qualquer componente de tensão,epsilon_kl, com qualquer componente de tensão, ou seja, \A lei de transformação coordenada para o tensor de rigidez de 4º grau é facilmente escrita em notação tensorial como

A equação tensorial direciona como escrever a transformação em notação matricial.
>

Sumário

A transformação coordenada de um vector na notação matricial e tensora é

>A transformação coordenada de um tensor na notação matricial e tensora é

Nota que {{\bf Q}} e {\lambda_{\ij}) são a mesma matriz de transformação.
Em 2-D, {{\bf Q}} e {\lambda_{ij}} são definidos como
]
que é um caso especial da forma 3-D mais geral
]