
Las matemáticas manejan una enorme cantidad de conceptos que son muy importantes pero, al mismo tiempo, complejos y requieren mucho tiempo. Sin embargo, Python proporciona la completa biblioteca SciPy que nos resuelve este problema. En este tutorial de SciPy, aprenderás a hacer uso de esta librería junto con algunas funciones y sus ejemplos.
Antes de continuar, echa un vistazo a todos los temas tratados en este artículo:
- ¿Qué es SciPy?
- NumPy vs SciPy
- Subpaquetes en SciPy
- Funciones Básicas
- Funciones Especiales
- Funciones de Integración
- Funciones de Optimización
- Funciones de Transformación de Fourier
- Funciones de Funciones de procesamiento de señales
- Álgebra lineal
- Eigenvalores dispersos
- Estructuras de datos espaciales y algoritmos
- Funciones de procesamiento de imágenes multidimensionales
- File IO
Así que vamos a empezar. 🙂
SciPy es una biblioteca de código abierto de Python que se utiliza para resolver problemas científicos y matemáticos. Está construida sobre la extensión NumPy y permite al usuario manipular y visualizar datos con una amplia gama de comandos de alto nivel. Como se mencionó anteriormente, SciPy se basa en NumPy y, por lo tanto, si se importa SciPy, no es necesario importar NumPy.
NumPy vs SciPy
Tanto NumPy como SciPy son bibliotecas de Python que se utilizan para el análisis matemático y numérico. NumPy contiene datos de arrays y operaciones básicas como ordenar, indexar, etc mientras que, SciPy consiste en todo el código numérico. Aunque NumPy proporciona una serie de funciones que pueden ayudar a resolver el álgebra lineal, las transformadas de Fourier, etc, SciPy es la biblioteca que realmente contiene las versiones completas de estas funciones junto con muchas otras. Sin embargo, si usted está haciendo el análisis científico utilizando Python, tendrá que instalar tanto NumPy y SciPy ya que SciPy se basa en NumPy.
Subpaquetes en SciPy:
SciPy tiene un número de subpaquetes para varios cálculos científicos que se muestran en la siguiente tabla:

Sin embargo, para una descripción detallada, puede seguir la documentación oficial.
Estos paquetes deben importarse exclusivamente antes de utilizarlos. Por ejemplo:
from scipy import cluster
Antes de ver cada una de estas funciones en detalle, vamos a echar un vistazo a las funciones que son comunes tanto en NumPy como en SciPy.
Interacción con NumPy:
SciPy se basa en NumPy y por lo tanto se puede hacer uso de las funciones propias de NumPy para manejar arrays. Para conocer en profundidad estas funciones, puede simplemente hacer uso de las funciones help(), info() o source().
help():
Para obtener información sobre cualquier función, puede hacer uso de la función help(). Hay dos formas de utilizar esta función:
- sin parámetros
- utilizando parámetros
Aquí hay un ejemplo que muestra los dos métodos anteriores:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
Cuando se ejecuta el código anterior, el primer help() devuelve la información sobre el submódulo del cluster. El segundo help() pide al usuario que introduzca el nombre de cualquier módulo, palabra clave, etc para el que desee buscar información. Para detener la ejecución de esta función, simplemente escriba ‘quit’ y pulse enter.
info():
Esta función devuelve información sobre las funciones, módulos, etc. deseados.
scipy.info(cluster)
source():
El código fuente se devuelve sólo para objetos escritos en Python. Esta función no devuelve información útil en caso de que los métodos u objetos estén escritos en cualquier otro lenguaje como C. Sin embargo en caso de que quieras hacer uso de esta función, puedes hacerlo de la siguiente manera:
scipy.source(cluster)
Funciones especiales:
SciPy proporciona una serie de funciones especiales que se utilizan en física matemática como la elíptica, funciones de conveniencia, gamma, beta, etc. Para buscar todas las funciones, se puede hacer uso de la función help() como se ha descrito anteriormente.
Funciones exponenciales y trigonométricas:
El paquete de funciones especiales de SciPy proporciona una serie de funciones a través de las cuales se pueden encontrar exponentes y resolver problemas trigonométricos.
Considera el siguiente ejemplo:
Ejemplo:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
Salida:
1000,0
8,0
1,0
0.7071067811865475
Hay muchas otras funciones presentes en el paquete de funciones especiales de SciPy que puedes probar por ti mismo.
Funciones de integración:
SciPy proporciona una serie de funciones para resolver integrales. Desde el integrador diferencial ordinario hasta el uso de reglas trapezoidales para calcular integrales, SciPy es un almacén de funciones para resolver todo tipo de problemas de integrales.
Integración general:
SiPy proporciona una función llamada quad para calcular la integral de una función que tiene una variable. Los límites pueden ser ( ) para indicar límites infinitos. La sintaxis de la función quad() es la siguiente:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Aquí, la función se integrará entre los límites a y b (también puede ser infinito).
EJEMPLO:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
En el ejemplo anterior, la función ‘a’ se evalúa entre los límites 0, 1. Al ejecutar este código, se verá la siguiente salida.
SALIDA:
(3.9086503371292665, 4.3394735994897923e-14)
Función integral doble:
SciPy proporciona dblquad que puede utilizarse para calcular integrales dobles. Una integral doble, como muchos sabemos, consta de dos variables reales. La función dblquad() tomará como parámetro la función a integrar junto con otras 4 variables que definen los límites y las funciones dy y dx.
EJEMPLO:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
SALIDA:
-1.33333333333335, 1.4802973661668755e-14)
SciPy proporciona varias otras funciones para evaluar integrales triples, integrales n, integrales de Romberg, etc que puedes explorar en detalle. Para encontrar todos los detalles sobre las funciones requeridas, utilice la función de ayuda.
Funciones de optimización:
El scipy.optimize proporciona una serie de algoritmos de optimización comúnmente utilizados que se pueden ver utilizando la función de ayuda. differential_evolution, dual_annealing, etc)
Función de Rosenbrook:
La función de Rosenbrook ( rosen) es un problema de prueba utilizado para los algoritmos de optimización basados en el gradiente. Se define como sigue en SciPy:

EJEMPLO:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
SALIDA: 7371.0399999999945
Nelder-Mead:
El método de Nelder-Mead es un método numérico utilizado a menudo para encontrar el mínimo/máximo de una función en un espacio multidimensional. En el siguiente ejemplo, se utiliza el método de minimización junto con el algoritmo de Nelder-Mead.
EJEMPLO:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
SALIDA: array()
Funciones de interpolación:
En el campo del análisis numérico, la interpolación se refiere a la construcción de nuevos puntos de datos dentro de un conjunto de puntos de datos conocidos. La biblioteca SciPy consiste en un subpaquete llamado scipy.interpolate que consta de funciones y clases spline, clases de interpolación unidimensional y multidimensional (univariante y multivariante), etc.
Interpolación univariante:
La interpolación univariante es básicamente un área de ajuste de curvas que encuentra la curva que proporciona un ajuste exacto a una serie de puntos de datos bidimensionales. SciPy proporciona la función interp1d que se puede utilizar para producir la interpolación univariante.
EJEMPLO:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
SALIDA:
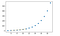
Interpolación multivariante:
La interpolación multivariante (interpolación espacial ) es un tipo de interpolación sobre funciones que constan de más de una variable. El siguiente ejemplo demuestra un ejemplo de la
Interpolación sobre una malla 2D utilizando la función interp2d(x, y, z) básicamente utilizará las matrices x, y, z para aproximar alguna función interp2d. f: «z = f(x, y)» y devuelve una función cuyo método de llamada utiliza la interpolación spline para encontrar el valor de los nuevos puntos.
EJEMPLO:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
SALIDA:

Funciones de la Transformada de Fourier:
El análisis de Fourier es un método que se ocupa de expresar una función como una suma de componentes periódicas y de recuperar la señal a partir de esas componentes. Las funciones fft pueden utilizarse para devolver la transformada discreta de Fourier de una secuencia real o compleja.
EJEMPLO:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
SALIDA:
De manera similar, se puede encontrar la inversa de ésta utilizando la función ifft de la siguiente manera:
EJEMPLO:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
SALIDA:
Funciones de procesamiento de señales:
El procesamiento de señales se ocupa de analizar, modificar y sintetizar señales como el sonido, las imágenes, etc. SciPy proporciona algunas funciones con las que se pueden diseñar, filtrar e interpolar datos unidimensionales y bidimensionales.
Filtrado:
Al filtrar una señal, básicamente se eliminan los componentes no deseados de la misma. Para realizar un filtrado ordenado, puede hacer uso de la función order_filter. Esta función básicamente realiza un filtrado ordenado en un array. La sintaxis de esta función es la siguiente:
SYNTAX:
filtro_orden(a, dominio, rango)
a = matriz de entrada de N dimensiones
dominio = matriz de máscara que tiene el mismo número de dimensiones que `a`
rango = Número no negativo que selecciona los elementos de la lista una vez ordenada (0 es el más pequeño seguido de 1…)
Ejemplo:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
Waveforms:
El subpaquete scipy.signal también consta de varias funciones que pueden utilizarse para generar formas de onda. Una de estas funciones es chirp. Esta función es un generador de coseno barrido en frecuencia y la sintaxis es la siguiente:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)
where,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
OUTPUT:

Álgebra lineal:
El álgebra lineal se ocupa de las ecuaciones lineales y sus representaciones utilizando espacios vectoriales y matrices. SciPy está construido sobre las librerías ATLAS LAPACK y BLAS y es extremadamente rápido en la resolución de problemas relacionados con el álgebra lineal. Además de todas las funciones de numpy.linalg, scipy.linalg también proporciona un número de otras funciones avanzadas. Además, si no se utiliza numpy.linalg junto con el soporte de ATLAS LAPACK y BLAS, scipy.linalg es más rápido que numpy.linalg.
Hallar la inversa de una matriz:
Matemáticamente, la inversa de una matriz A es la matriz tal que donde es la matriz identidad que consiste en unos por la diagonal principal denotada como B=A-1. En SciPy, esta inversa se puede obtener utilizando el método linalg.inv.
Ejemplo:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
Salida:
]
Hallar los determinantes:
El valor derivado aritméticamente de los coeficientes de la matriz se conoce como el determinante de una matriz cuadrada. En SciPy, esto se puede hacer utilizando una función det que tiene la siguiente sintaxis:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
donde,
a : (M, M) es una matriz cuadrada
sobreescribir_a( bool, opcional) : Permite sobrescribir los datos de a
comprobar_finito ( bool, opcional): Comprobar si la matriz de entrada está formada sólo por números finitos
Ejemplo:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
Salida: -5,0
Eigenvalores dispersos:
Los valores propios son un conjunto específico de escalares ligados a ecuaciones lineales. El ARPACK proporciona que le permiten encontrar los valores propios ( eigenvectores ) bastante rápido. La funcionalidad completa de ARPACK está empaquetada dentro de dos interfaces de alto nivel que son scipy.sparse.linalg.eigs y scipy.sparse.linalg.eigsh. eigs. La interfaz eigs permite encontrar los valores propios de matrices cuadradas reales o complejas no simétricas mientras que la interfaz eigsh contiene interfaces para matrices reales-simétricas o complejas-hermitianas.
La función eigh resuelve un problema generalizado de valores propios para una matriz compleja hermitiana o real simétrica.
Ejemplo:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
Salida:
Valores propios seleccionados :
Complex ndarray :
]
Estructuras de datos espaciales y algoritmos:
Los datos espaciales consisten básicamente en objetos que están formados por líneas, puntos, superficies, etc. El paquete scipy.spatial de SciPy puede calcular diagramas de Voronoi, triangulaciones, etc. utilizando la biblioteca Qhull. También consta de implementaciones de KDTree para consultas de puntos más cercanos.
Triangulaciones de Delaunay:
Matemáticamente, las triangulaciones de Delaunay para un conjunto de puntos discretos en un plano es una triangulación tal que ningún punto del conjunto de puntos dado está dentro de la circunferencia de ningún triángulo.
EJEMPLO:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
SALIDA:

Funciones de procesado de imágenes multidimensionales:
El procesado de imágenes trata básicamente de realizar operaciones sobre una imagen para recuperar información u obtener una imagen mejorada a partir de la original. El paquete scipy.ndimage consta de una serie de funciones de procesamiento y análisis de imágenes diseñadas para trabajar con matrices de dimensionalidad arbitraria.
Convolución y correlación:
SciPy proporciona una serie de funciones que permiten la correlación y convolución de imágenes.
- La función correlate1d puede utilizarse para calcular la correlación unidimensional a lo largo de un eje dado
- La función correlate permite la correlación multidimensional de cualquier matriz dada con el kernel especificado
- La función convolve1d puede utilizarse para calcular laLa función convolve1d puede utilizarse para calcular la convolución unidimensional a lo largo de un eje dado
- La función convolve permite la convolución multidimensional de cualquier matriz dada con el núcleo especificado
Ejemplo:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
OUTPUT: array()
File IO:
El paquete scipy.io proporciona una serie de funciones que le ayudan a gestionar archivos de diferentes formatos como archivos de MATLAB, archivos IDL, archivos de Matrix Market, etc.
Para hacer uso de este paquete, tendrá que importarlo de la siguiente manera:
import scipy.io as sio
Para obtener información completa sobre el subpaquete, puede consultar el documento oficial sobre File IO.
Con esto llegamos al final de este tutorial de SciPy. Espero que hayas entendido todo con claridad. Asegúrese de practicar tanto como sea posible.
Si usted desea comprobar más artículos sobre las tecnologías más de tendencia del mercado como la Inteligencia Artificial, DevOps, Hacking Ético, entonces usted puede referirse al sitio oficial de Edureka.
Esté atento a otros artículos de esta serie que explicará los diversos otros aspectos de Python y Ciencia de Datos.
1. Clasificador de aprendizaje automático en Python
2. Hoja de trucos de Python Scikit-Learn
3. Herramientas de aprendizaje automático
4. Bibliotecas de Python para ciencia de datos y aprendizaje automático
5. Chatbot en Python
6. Colecciones en Python
7. Módulos en Python
8. Habilidades de desarrollador en Python
9. Preguntas y respuestas de la entrevista de OOPs
10. Curriculum Vitae Para Un Desarrollador De Python
11. Análisis exploratorio de datos en Python
12. Juego de la serpiente con el módulo tortuga de Python
13. Salario de un desarrollador de Python
14. Análisis de componentes principales
15. Python vs C++
16. Tutorial de Scrapy
17. Web Scraping con Python
18. Método de regresión por mínimos cuadrados
19. Jupyter Notebook Cheat Sheet
20. Conceptos básicos de Python
21. Programas de patrones en Python
22. Generadores en Python
23. Decorador en Python
24. Python Spyder IDE
25. Aplicaciones móviles usando Kivy en Python
26. Los 10 mejores libros para aprender & a practicar Python
27. Framework de Robots con Python
28. Juego de la serpiente en Python usando PyGame
29. Preguntas y respuestas de la entrevista de Django
30. Las 10 mejores aplicaciones en Python
31. Tablas Hash y Hashmaps en Python
32. Python 3.8
33. Máquina de vectores de apoyo
34. Tutorial de Python