Hur man förbereder sig för geometrifrågorna på ett matteprov
Allmän information
Geometri är bara ett fint namn för studiet av linjer och former. Det finns säkert ytterligare svåra principer och ämnen, men vi har grunderna här. Du måste behärska dessa innan du tar dig an mer avancerade begrepp.
(Observera att om en figur är märkt ”exempel” i den här guiden är det inte nödvändigtvis den enda representationen av den figuren, men den är en av dem.)
Punkter och linjer
En punkt i geometri är en plats. Den har ingen längd, bredd eller djup. Vi använder en punkt och en stor bokstav för att visa en punkt.
En linjesträckning definieras av två punkter och alla punkter mellan dem. De två punkterna kallas för segmentets ändpunkter. Ett segment har en dimension: längd. För att skriva ett segment placerar du ett streck över de två ändpunkterna. \(\overline{AB}\) eller \(\overline{BA}\) är detta segment:

En linje sträcker sig i båda riktningarna utan slut. För att skriva en linje placerar du en stapel med två pilar över två punkter på linjen. \(\overleftrightarrow{AB}\) eller \(\overleftrightarrow{BA}\) är linjen:

En stråle börjar i en ändpunkt och sträcker sig utan slut i endast en riktning. För att skriva en stråle placerar du en stapel med en pil som pekar åt höger över två punkter: slutpunkten och någon annan punkt (i den riktningen). \(\overrightarrow{AB}\) är strålen:

Notera: du kan inte skriva en stråle med pilen pekande åt vänster som \(\overleftarrow{BA}\). Dessutom är ordningen viktig. \(\overrightarrow{BA}\) är inte samma sak som \(\overrightarrow{AB}\). Den första bokstaven är alltid startpunkten för en stråle.
Två linjer, segment eller strålar är vinkelräta om de bildar en rät vinkel (se nedan). Använd symbolen \(\perp\) för att beteckna vinkelrätthet. Om till exempel \(\overline{AB}\) är vinkelrätt mot \(\overline{CD}\) kan man skriva \(\overline{AB} \perp \overline{CD}\).
Exempel: 
Två linjer är parallella om de aldrig skär varandra. Om \(\overleftrightarrow{AB}\) är parallell med \(\overleftrightarrow{CD}\) kan man skriva \(\overleftrightarrow{AB} \parallel \overleftrightarrow{CD}\).
Exempel: 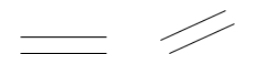
Planformer
I geometrin är ett plan en platt tvådimensionell yta som sträcker sig oändligt långt. De två dimensionerna är längd och bredd. Plana former är alltså ”platta” former, som t.ex. kvadrater, cirklar och trianglar.
Gemensamma former
En polygon är en sluten yta på ett plan som avgränsas av linjesträckor som kallas sidor.
Exempel: 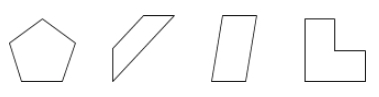
En regelbunden polygon är en polygon där alla segment och inre vinklar är kongruenta.
Exempel:
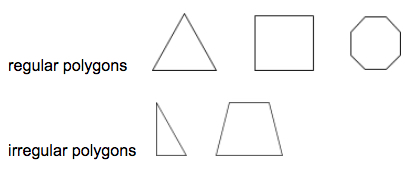
En triangel är en polygon med tre sidor.
Exempel:
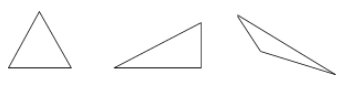
Quadrilateraler – fyrsidiga polygoner
En parallellogram är en typ av fyrhörning där motsatta sidor är parallella och kongruenta. Motsatta vinklar i en parallellogram är också kongruenta.
Exempel: 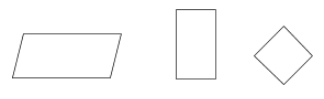
En rektangel är en parallellogram med fyra räta vinklar.
Exempel: 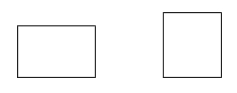
En romb är en parallellogram där alla fyra sidorna är kongruenta.
Exempel: 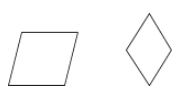
En kvadrat är en parallellogram som är både en romb och en rektangel (alla sidor är kongruenta och alla vinklar är räta).
Exempel: 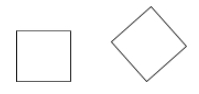
En trapets är en fyrhörning med endast ett par parallella sidor.
Exempel: 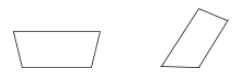
Polygoner med fler än fyra sidor
\
\(^1\) En polygon med 11 sidor kan också kallas en endekagon eller en odekagon.
Mätning av former
Umkretsen är det totala avståndet runt en polygon. För att hitta omkretsen är det bara att addera längderna på alla sidor. Om polygonen är regelbunden (alla sidor är kongruenta) och längden på en sida är \(s\), multiplicera antalet sidor med \(s\) för att hitta omkretsen. Till exempel är omkretsen för en regelbunden femhörning \(P_\text{reg pentagon}=5s\)
.