
Neurala nätverk och matematik går inte att skilja åt, och det är förmodligen det som skrämmer de flesta. Jag har hört alltför många tveksamma kommentarer om Deep Learning: ”Det här är för mycket matematik för mig att förstå”, ”Hur många företag använder verkligen Deep Learning? Jag sparar hellre hjärnspöken och håller mig borta från dessa krävande begrepp”.
Men om man tänker efter är det inte så svårt. Lita på mig! För att förstå varför en algoritm beter sig på ett visst sätt är det viktigt att förstå vad som händer bakom kulisserna. Komplexa algoritmer för maskininlärning är paketerade på ett bekvämt sätt för oss i dag och är bara ett funktionssamtal bort. Aktiveringsfunktionernas derivat är något mindre uppenbara begrepp som vi ofta tenderar att ignorera. De utgör dock grunden för kraftfulla algoritmer och det lönar sig verkligen att lägga lite extra arbete på att förstå dem. Efter att ha läst den här artikeln kommer du att vara ett steg närmare att reda ut vad som ligger bakom fasaden av den ”svarta lådan”.
Bakgrund
Neurala nätverk använder en mängd olika aktiveringsfunktioner i de dolda och utgående lagren för att katalysera inlärningsprocessen. Några vanligt förekommande aktiveringsfunktioner är Sigmoid- och tanH-funktionerna. Den mest populära aktiveringsfunktionen är ReLU ( Rectified Linear Unit) på grund av dess förmåga att effektivt övervinna problemet med försvinnande gradient. En djupgående inblick i aktiveringsfunktioner är för en annan dag. Idag kommer vi att fokusera på matematiken bakom Sigmoidfunktionens derivat.
Varför är derivatet av en aktiveringsfunktion viktigt?
Som du säkert vet är det två steg som driver neurala nätverk:
- Forward Propagation – Ingångsdata flödar genom nätverket och vi får det förutsagda resultatet. Vi jämför den med den faktiska utgången och beräknar felet.
- Backpropagation – Det beräknade felet används för att uppdatera det neurala nätverkets parametrar med hjälp av aktiveringsfunktionens derivat.
Den sigmoida funktionen
Den sigmoida funktionen, som kännetecknas av en S-formad kurva, kallas ofta för ett specialfall av den logistiska funktionen. Den är mest användbar i fall där vi måste förutsäga sannolikhet som utdata.
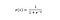
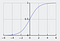
Sigmoidfunktionen ger ut värden som ligger mellan 0 och 1 (med rätta med tanke på att den förutsäger sannolikheter).
Den sigmoida derivatan
Denna grundläggande byggsten som hjälper till att träna neurala nätverk har formen:


Omedelbart, låt oss sätta igång med derivationen!
Ansats 1

Ansats 2:
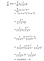
Varför använder vi denna version av derivatet?
I det framåtriktade propagationssteget beräknar du den sigmoida funktionen (σ(x)) och har dess värde till hands. När du beräknar derivatan i backpropagationssteget behöver du bara sätta in värdet av σ(x) i formeln som härletts ovan och voila, du är klar!
Det var allt, killar! Tack för att ni läste!