Cómo pensar con exponentes y logaritmos

Aquí hay un truco para pensar en problemas que implican exponentes y logaritmos. Sólo hay que hacerse dos preguntas:

1) ¿Estamos hablando de entradas (causa del cambio) o de salidas (el cambio real que ha ocurrido?)

Los logaritmos revelan las entradas que causaron el crecimiento
Los exponentes encuentran el resultado final del crecimiento

2) ¿Estamos hablando de la perspectiva del cultivador, o de la de un observador?

e y el logaritmo natural son desde la perspectiva del cultivador instante a instante
Base 10, Base 2, etc. son medidas convenientes para un observador humano

En mi cabeza, pongo las opciones en una tabla:

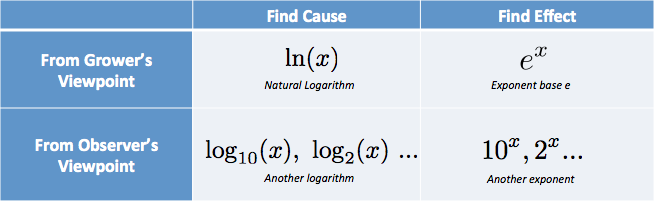
exponente logaritmo punto de vista comparación

Tengo pensamientos como «necesito la causa, desde la perspectiva del cultivador… que es el logaritmo natural». (El logaritmo natural se abrevia con minúscula LN, del logarithmus naturalis de alta calidad.)

Me frustraron las clases que describían la parte interna de la tabla, las funciones brutas, sin los pies de foto que explicaban cuándo usarlas

Eso no va a volar, vamos a practicar directamente el pensamiento con logaritmos y exponentes.

Escenario: Describiendo el crecimiento del PIB

Aquí tenemos un ejemplo típico de crecimiento:

De 2000 a 2010, el PIB de Estados Unidos pasó de 9,9 billones a 14,4 billones

Ok, claro, esos números muestran que el cambio ocurrió. Pero probablemente queramos saber la causa: ¿Qué tasa de crecimiento anual promedio explicaría este cambio?

Inmediatamente, mi cerebro piensa en «logaritmos» porque estamos trabajando hacia atrás desde el crecimiento hasta la tasa que lo causó. Empiezo con un pensamiento como este:

$displaystyle{{text{logaritmo del cambio} \N - flecha derecha \N - texto {causa del crecimiento} }$

Un buen comienzo, pero afinémoslo.

Primero, ¿qué logaritmo debemos usar?

Por defecto, elijo el logaritmo natural. La mayoría de los eventos terminan siendo en términos del cultivador (no del observador), y me gusta «montar junto con» el elemento de crecimiento para visualizar lo que está sucediendo. (Los radianes son similares: miden los ángulos en términos de quien los mueve.)

Siguiente pregunta: ¿a qué cambio aplicamos el logaritmo?

En realidad sólo nos interesa la relación entre el inicio y el final: de 9,9 billones a 14,4 billones en 10 años. Esta es la misma tasa de crecimiento que pasar de \$9,90 a \$14,40 en el mismo período.

Podemos afinar nuestro pensamiento:

${displaystyle{{text{logaritmo natural de la relación de crecimiento} \N - flecha derecha \N - texto {causa del crecimiento}$

$\displaystyle{{ln(\frac{14,4}{9,9}) = .374}$

Ok, la causa fue una tasa de .374 o 37,4%. ¿Hemos terminado?

Todavía no. Los logaritmos no saben sobre el tiempo que duró un cambio (no enchufamos 10 años, ¿verdad?). Nos dan una tasa como si todo el cambio ocurriera en un solo periodo de tiempo.

El cambio podría ser, efectivamente, un solo año de crecimiento continuo del 37,4%, o 2 años de crecimiento del 18,7%, o alguna otra combinación.

Desde el escenario, sabemos que el cambio se produjo en 10 años, por lo que la tasa debe haber sido:

${displaystyle{{text{rate}} ={frac{.374}{10}{0,0374}{3,74%}$

Desde el punto de vista del crecimiento instantáneo y continuo, la economía estadounidense creció un 3,74% al año.

¿Hemos terminado? No del todo.

Esta tasa continua es desde la perspectiva del crecimiento, como si estuviéramos «cabalgando» con la economía a medida que cambia. Un banquero probablemente se preocupa por la diferencia humana, año tras año. Podemos averiguar esto dejando que el crecimiento continuo se ejecute durante un año:

${displaystyle{{text}{exponente con tasa y tiempo} \N - Flecha derecha \N - Efecto del crecimiento. }$

$\displaystyle{e^{\text{rate} \cdot \text{time}} = \text{growth}}$

$\displaystyle{e^{0,0374 \cdot 1}} = 1,0381}$

La ganancia interanual es del 3,8%, ligeramente superior a la tasa instantánea del 3,74% debido a la capitalización. Esta es otra forma de decirlo:

Desde una base instantánea, una parte determinada de la economía está creciendo un 3,74%, modelado por $e^(.0374 * años)$
En una base anual, con los efectos compuestos calculados, la economía crece un 3,81%, modelado por $1,0381^años$

En finanzas, podemos querer el cambio de año en año que puede ser comparado bien con otras tendencias. En ciencia e ingeniería, preferimos modelar el comportamiento sobre una base instantánea.

Escenario: Describiendo el crecimiento natural

Detesto los ejemplos artificiosos como «Suponga que las bacterias se duplican cada 24 horas, encuentre su fórmula de crecimiento». ¿Las colonias de bacterias se replican en intervalos humanos limpios, y esperamos a que se duplique exactamente?

Un escenario mejor: «Oye, he encontrado unas bacterias, he esperado una hora, y el bulto ha crecido de 2,3 gramos a 2,32 gramos. Me voy a comer ahora. Calcula cuánto tendremos cuando vuelva en 3 horas».

Modelemos esto. Necesitaremos un logaritmo para encontrar la tasa de crecimiento, y luego un exponente para proyectar ese crecimiento hacia adelante. Al igual que antes, vamos a mantener todo en términos del logaritmo natural para empezar.

El factor de crecimiento es:

$\displaystyle{{text{logaritmo del cambio} \N - flecha derecha \N - texto {causa del crecimiento}$

$\displaystyle{{ln(\text{crecimiento}) = \ln(2,32/2,3) = .0086 = .86\%}$

Esa es la tasa para una hora, y el modelo general para proyectar hacia adelante será

$\displaystyle{text}{exponente con tasa y tiempo} \N - Flecha derecha \N - Efecto del crecimiento.$

$<displaystyle{{e^{.0086{cdot{{text{horas}} \N - Flecha derecha \N - Efecto del crecimiento. }$

Si empezamos con 2,32 y crecemos durante 3 horas tendremos:

$\displaystyle{2,32 \cdot e^{.0086 \cdot 3} = 2,38}$

Sólo por diversión, ¿cuánto tiempo pasa hasta que la bacteria se duplica? Imagina que esperas a que 1 se convierta en 2:

$displaystyle{1 \cdot e^{.0086 \cdot \text{hours}} = 2}$

Podemos tomar mecánicamente el logaritmo natural de ambos lados para «deshacer el exponente», pero pensemos intuitivamente.

Si 2 es el resultado final, entonces ln(2) es la entrada de crecimiento que nos llevó allí (alguna tasa × tiempo). Sabemos que la tasa fue de 0,0086, por lo que el tiempo para llegar a 2 sería:

${displaystyle{{text{horas} ={frac{ln(2)}{text{tasa}} ={frac{.693}{.0086} = 80,58}$

La colonia se duplicará después de ~80 horas. (¿Te alegras de no haberte quedado?)

¿Qué significa realmente el cambio de perspectiva?

Descubrir si quieres la entrada (causa del crecimiento) o la salida (resultado del crecimiento) es bastante sencillo. Pero, ¿cómo se visualiza la perspectiva del cultivador?

Imagina que tenemos pequeños trabajadores que están construyendo el patrón de crecimiento final (ver el artículo sobre los exponentes):

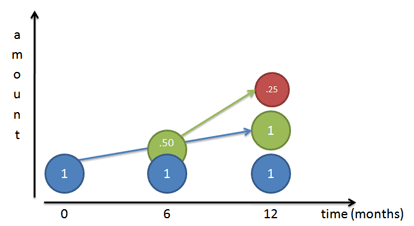
$interés compuesto$

Si nuestra tasa de crecimiento es del 100%, le estamos diciendo a nuestro trabajador inicial (el Sr. Azul) que trabaje con constancia y cree una copia del 100% de sí mismo al final del año. Si lo seguimos día a día, vemos que sí termina una copia de sí mismo al 100% (el Sr. Verde) al final del año.

Pero… ese trabajador que estaba construyendo (el Sr. Verde) empieza a trabajar también. Si el Sr. Verde aparece por primera vez a los 6 meses, tiene medio año para trabajar (mismo ritmo anual que el Sr. Azul) y construye al Sr. Rojo. Por supuesto, el Sr. Rojo acaba estando a medias, ya que el Sr. Verde sólo tiene 6 meses.

¿Y si el Sr. Verde apareciera a los 4 meses? ¿Un mes? ¿Un día? ¿Un segundo? Si los trabajadores empiezan a crecer inmediatamente, obtenemos la curva instante a instante definida por $e^x$:

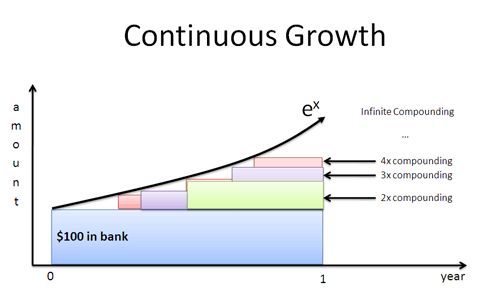
crecimiento continuo

El logaritmo natural da una tasa de crecimiento en términos de la perspectiva de un trabajador individual. Introducimos esa tasa en $e^x$ para encontrar el resultado final, con toda la capitalización incluida.

Usando otras bases

Cambiar a otro tipo de logaritmo (base 10, base 2, etc.) significa que estamos buscando algún patrón en el crecimiento global, no lo que el trabajador individual está haciendo.

Cada logaritmo hace una pregunta al ver un cambio:

Log base e: ¿Cuál fue el ritmo instantáneo seguido por cada trabajador?
Log base 2: ¿Cuántas duplicaciones fueron necesarias?
Log base 10: ¿Cuántas 10x fueron necesarias?

Aquí tienes un escenario para analizar:

En 30 años, el número de transistores de los chips típicos pasó de 1000 a 1000 millones

¿Cómo analizarías esto?

Los microchips no son una entidad única que crece suavemente con el tiempo. Son ediciones separadas, de empresas que compiten entre sí, e indican una tendencia tecnológica general.
Ya que no estamos «cabalgando» con un microchip en expansión, usemos una escala hecha para la comodidad humana. Duplicar es más fácil de pensar que 10x-ing.

Con estas suposiciones obtenemos:

$displaystyle{{text{logaritmo del cambio} \N - flecha derecha \N - texto {causa del crecimiento}$

$estilo de visualización {log_2(\frac{text{1 billón}}{1000}) = \log_2(\text{1 millón}) \sim \text{20 duplicaciones}}$

La «causa del crecimiento» fue 20 duplicaciones, que sabemos ocurrieron en 30 años. Esto supone una media de 2/3 duplicaciones por año, o 1,5 años por duplicación, una buena regla general.

Desde la perspectiva del cultivador, calcularíamos $\ln(\text{mil millones}/1000) / \text{30 años} = 46\%$ de crecimiento continuo (un poco más difícil de relacionar en este escenario).

Podemos resumir nuestro análisis en una tabla:

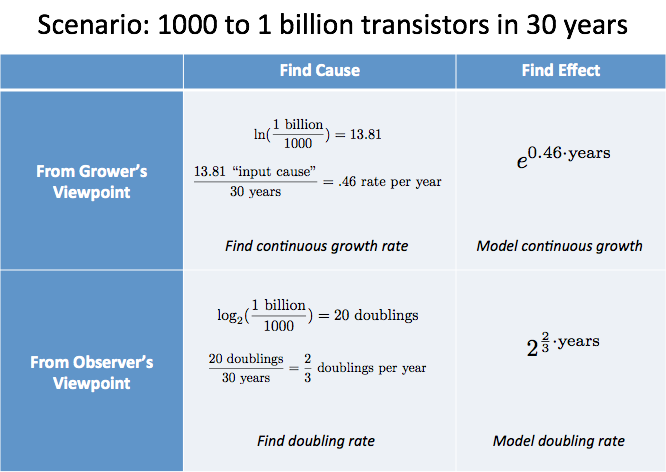
ejemplo de transistor de exponentes

Resumen

El aprendizaje consiste en encontrar las leyendas ocultas detrás de un concepto. ¿Cuándo se utiliza? ¿Qué punto de vista aporta al problema?

Mi interpretación actual es que los exponentes preguntan por la causa frente al efecto y el cultivador frente al observador. Pero nunca hemos terminado; parte de la diversión es ver cómo podemos recapitular viejos conceptos.

Felices matemáticas.

Apéndice: La fórmula del cambio de base

Aquí tienes cómo pensar en el cambio de base. Suponiendo una tasa de crecimiento continua del 100%,

ln(x) es el tiempo para crecer hasta x
ln(2) es el tiempo para crecer hasta 2

Dado que tenemos el tiempo para duplicar, podemos ver cuántos «cabrían» en el tiempo total para crecer hasta x:

${displaystyle{{número de duplicaciones de 1 a x}} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

Por ejemplo, ¿cuántas duplicaciones se producen de 1 a 64?

Bueno, ln(64) = 4,158. Y ln(2) = 0,693. El número de dobleces que encajan es:

$Displaystyle{{ln(64)}{ln(2)} = \frac{4,158}{.693} = 6}$

En el mundo real, las calculadoras pueden perder precisión, así que hay que utilizar una función logarítmica directa de base 2 si es posible. Y por supuesto, podemos tener un número fraccionario: Pasar de 1 a la raíz cuadrada de 2 es «la mitad» de una duplicación, o log2(1,414) = 0,5.

Cambiar a logaritmo de base 10 significa que estamos contando el número de 10x-ings que encajan:

${displaystyle{{text{número de 10x-ings de 1 a x} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Bueno, ¿verdad? Lee Uso de logaritmos en el mundo real para ver más ejemplos.

Otros posts de esta serie

Una guía intuitiva de las funciones exponenciales & e
Demistificando el logaritmo natural (ln)
Una guía visual de los tipos de interés simples, compuestos y continuos
Definiciones comunes de e (coloreadas)
Entendiendo los exponentes (¿Por qué 0^0 = 1?)
Usando logaritmos en el mundo real
Cómo pensar con exponentes y logaritmos
Entendiendo el crecimiento discreto frente al continuo
¿Qué significa realmente un exponente?
Pregunta: ¿Por qué e es especial? (2,718…, no 2, 3,7 u otro número?)