Jak myslet pomocí exponentů a logaritmů

Tady je trik, jak přemýšlet nad problémy zahrnujícími exponenty a logaritmy. Stačí si položit dvě otázky:

1) Mluvíme o vstupech (příčině změny) nebo výstupech (skutečné změně, která nastala?)

Logaritmy odhalují vstupy, které způsobily růst
Exponenty zjišťují konečný výsledek růstu

2) Mluvíme o pohledu pěstitele, nebo pozorovatele?

e a přirozený logaritmus jsou z pohledu pěstitele okamžik po okamžiku
základ 10, základ 2 atd. jsou měření vhodná pro lidského pozorovatele

V hlavě si dávám možnosti do tabulky:

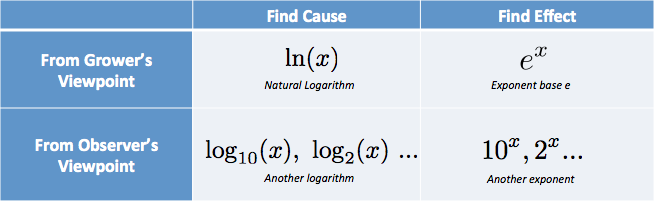
srovnání logaritmů z pohledu pěstitele

Mám myšlenky typu: „Potřebuji příčinu, z pohledu pěstitele… to je přirozený log.“. (Přirozený logaritmus se zkracuje s malým písmenem LN, od vznešeného logaritmus naturalis.)

Frustrovaly mě hodiny, které popisovaly vnitřní část tabulky, surové funkce, bez popisků, které vysvětlovaly, kdy je použít!“

To neprojde, pojďme si přímo procvičit myšlení s logaritmy a exponenty.

Scénář: Popis růstu HDP

Tady je typický příklad růstu:

Od roku 2000 do roku 2010 se HDP USA změnil z 9,9 bilionu na 14,4 bilionu

Ok, jasně, ta čísla ukazují, že ke změně došlo. Ale my asi chceme nahlédnout do příčiny: Jaké průměrné roční tempo růstu by tuto změnu způsobilo?

Můj mozek okamžitě napadne „logaritmy“, protože se od růstu dostáváme zpětně k tempu, které ho způsobilo. Začínám myšlenku takto:

$\displaystyle{\text{logaritmus změny}. \pravá šipka \text{příčina růstu} }$

Dobrý začátek, ale pojďme ho vybrousit.

Nejprve, který logaritmus bychom měli použít?

Standardně volím přirozený logaritmus. Většina událostí skončí v termínech rostoucího prvku (ne pozorovatele) a já se rád „svezu“ s rostoucím prvkem, abych si mohl vizualizovat, co se děje. (Radiány jsou podobné: měří úhly z hlediska hybatele.)

Další otázka: na jakou změnu použijeme logaritmus?

Ve skutečnosti nás zajímá jen poměr mezi začátkem a koncem: 9,9 bilionu na 14,4 bilionu za 10 let. To je stejná míra růstu, jako kdybychom za stejné období přešli z \9,90 na \14,40 dolaru.

Můžeme naši úvahu zaostřit:

$\displaystyle{\text{přirozený logaritmus poměru růstu} \pravá šipka \text{příčina růstu} }$

$\displaystyle{\ln(\frac{14,4}{9,9}) = ,374}$

Ok, příčinou byla míra .374 neboli 37,4 %. Skončili jsme?

Ještě ne. Logaritmy neví o tom, jak dlouho změna trvala (nezapojili jsme 10 let, že?). Uvádějí nám míru, jako by se celá změna odehrála v jediném časovém období.

Změna skutečně může být jediný rok nepřetržitého růstu o 37,4 %, nebo 2 roky růstu o 18,7 %, nebo nějaká jiná kombinace.

Ze scénáře víme, že změna trvala 10 let, takže tempo muselo být:

$\displaystyle{ \text{rate} = \frac{.374}{10} = ,0374 = 3,74\%}$

Z pohledu okamžitého, nepřetržitého růstu rostla ekonomika USA o 3,74 % ročně.

Jsme hotovi? Ne tak docela!

Toto nepřetržité tempo je z pohledu růstu, jako bychom se „vezli“ spolu s ekonomikou při jejích změnách. Bankéře pravděpodobně zajímá lidsky přívětivý, meziroční rozdíl. To můžeme zjistit tak, že necháme průběžný růst běžet po dobu jednoho roku:

$\displaystyle{\text{exponent s mírou a časem} \pravá šipka \text{důsledek růstu} }$

$\displaystyle{e^{\text{rate} \cdot \text{čas}} = \text{růst}}$

$\displaystyle{e^{.0374 \cdot 1} = 1,0381}$

Celoroční přírůstek je 3,8 %, což je o něco více než okamžitá míra 3,74 % v důsledku skládání. Zde je jiný způsob vyjádření:

Z okamžitého hlediska roste daná část ekonomiky o 3,74 %, modelováno pomocí $e^(.0374 * let)$
Z roku na rok, s rozpracovanými složenými efekty, roste ekonomika o 3,81 %, modelováno pomocí $1,0381^let$

V oblasti financí můžeme chtít meziroční změnu, kterou lze pěkně porovnat s jinými trendy. Ve vědě a technice dáváme přednost modelování chování na okamžité bázi.

Scénář: Popis přirozeného růstu

Nesnáším vymyšlené příklady typu „Předpokládejme, že se bakterie zdvojnásobí každých 24 hodin, najděte vzorec jejího růstu.“. Replikují se kolonie bakterií v čistě lidských intervalech a máme čekat na přesné zdvojnásobení?“

Lepší scénář: „Hele, našel jsem nějakou bakterii, počkal jsem hodinu a hrouda vyrostla z 2,3 gramu na 2,32 gramu. Teď jdu na oběd. Zjistěte, kolik toho budeme mít, až se za 3 hodiny vrátím.“

Představme si to jako model. Budeme potřebovat logaritmus, abychom zjistili rychlost růstu, a pak exponent, abychom tento růst promítli do budoucnosti. Stejně jako dříve ponechme pro začátek vše v přirozeném logaritmu.

Faktor růstu je:

$\displaystyle{\text{logaritmus změny} \pravá šipka \text{příčina růstu} }$

$\displaystyle{\ln(\text{růst}) = \ln(2,32/2,3) = ,0086 = ,86\%}$

To je míra za jednu hodinu a obecný model pro projekci do budoucna bude

$\displaystyle{\text{výraz s mírou a časem} \pravá šipka \text{vliv růstu} }$

$\displaystyle{e^{.0086 \cdot \text{hodiny}} \rightarrow \text{efekt růstu} }$

Pokud začneme s hodnotou 2,32 a budeme růst 3 hodiny, dostaneme:

$\displaystyle{2,32 \cdot e^{.0086 \cdot 3} = 2,38}$

Jen pro zajímavost, za jak dlouho se bakterie zdvojnásobí? Představte si, že čekáte, až se 1 změní na 2:

$\displaystyle{1 \cdot e^{.0086 \cdot \text{hodin}} = 2}$

Můžeme mechanicky vzít přirozený logaritmus obou stran, abychom „zrušili exponent“, ale uvažujme intuitivně.

Jestliže 2 je konečný výsledek, pak ln(2) je růstový vstup, který nás tam dostal (nějaká rychlost × čas). Víme, že rychlost byla 0,0086, takže čas, za který se dostaneme na 2, bude:

$\displaystyle{ \text{hodin} = \frac{\ln(2)}{\text{rychlost}} = \frac{.693}{.0086} = 80,58}$

Kolonie se zdvojnásobí po ~80 hodinách. (Jste rádi, že jste se nezdrželi?)

Co vlastně znamená změna perspektivy?“

Zjistit, zda chcete vstup (příčinu růstu) nebo výstup (výsledek růstu), je celkem jednoduché. Jak si ale představit perspektivu pěstitele?“

Představme si, že máme malé dělníky, kteří budují výsledný růstový obrazec (viz článek o exponentech):

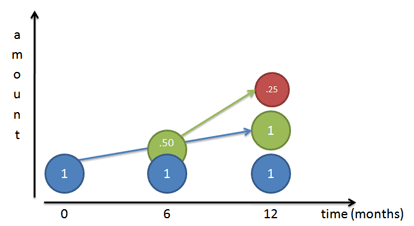
$složené úročení$

Pokud je naše míra růstu 100 %, říkáme našemu počátečnímu dělníkovi (panu Modrému), aby soustavně pracoval a do konce roku vytvořil 100 % kopii sebe sama. Sledujeme-li ho den po dni, vidíme, že na konci roku skutečně dokončí 100% kopii sebe sama (pana Zeleného).

Ale… ten pracovník, kterého vytvářel (pan Zelený), začne pracovat také. Jestliže se pan Zelený poprvé objeví v 6 měsících, má na práci půl roku (stejnou roční sazbu jako pan Modrý) a postaví pana Červeného. Samozřejmě, že pan Červený skončí napůl hotový, protože pan Zelený má jen 6 měsíců.

Co kdyby se pan Zelený objevil po 4 měsících? Měsíc? Za den? Za vteřinu? Jestliže pracovníci začnou růst okamžitě, dostaneme křivku okamžitého růstu definovanou vztahem $e^x$:

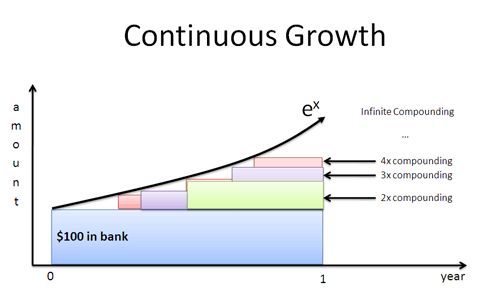
kontinuální růst

Přirozený logaritmus udává tempo růstu z hlediska individuálního pracovníka. Zapojíme-li toto tempo do $e^x$, zjistíme konečný výsledek se započtením všech složení.

Použití jiných základů

Přechod na jiný typ logaritmu (základ 10, základ 2 atd.) znamená, že hledáme nějakou zákonitost celkového růstu, nikoli to, co dělá jednotlivý pracovník.

Každý logaritmus si při pozorování změny klade otázku:

Log. základ e: Jakou okamžitou rychlost sledoval každý pracovník?
Log base 2: Kolik zdvojnásobení bylo potřeba?
Log base 10: Kolik desetinásobků bylo potřeba?

Tady je scénář k analýze:

V průběhu 30 let se počet tranzistorů na typických čipech zvýšil z 1000 na 1 miliardu

Jak byste to analyzovali?

Mikročipy nejsou jeden celek, který v čase plynule roste. Jsou to samostatné edice, od konkurenčních společností, a naznačují obecný technologický trend.
Protože se „nevezeme“ s expandujícím mikročipem, použijme měřítko vytvořené pro lidské pohodlí. O zdvojnásobení je snazší přemýšlet než o desetinásobení.

S těmito předpoklady dostaneme:

$\displaystyle{\text{logaritmus změny} \pravá šipka \text{příčina růstu} }$

$\displaystyle{\log_2(\frac{\text{1 miliarda}}{1000}) = \log_2(\text{1 milion}) \sim \text{20 zdvojnásobení}}$

„Příčinou růstu“ bylo 20 zdvojnásobení, která, jak víme, nastala za 30 let. To jsou v průměru 2/3 zdvojnásobení za rok, neboli 1,5 roku na jedno zdvojnásobení – pěkné pravidlo.

Z pohledu pěstitele bychom vypočítali $\ln(\text{1 miliarda}/1000) / \text{30 let} = 46\%$ nepřetržitého růstu (v tomto scénáři je to trochu těžší).

Naši analýzu můžeme shrnout do tabulky:

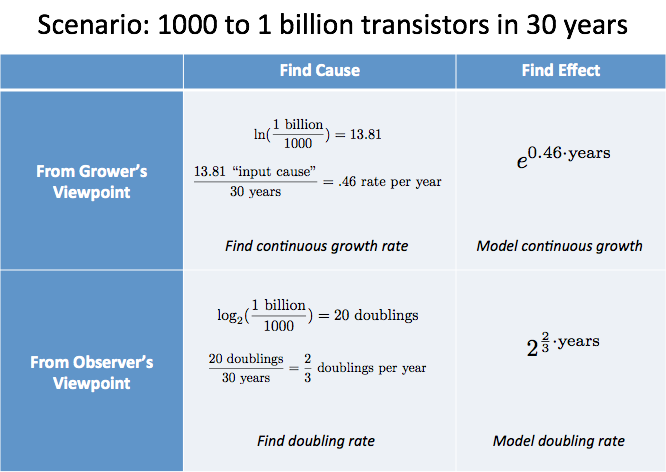
exponenty tranzistoru příklad

Shrnutí

Učení je o hledání skrytých popisků za pojmem. Kdy se používá? Jaký úhel pohledu přináší do problému?

Můj současný výklad je, že exponenty se ptají na příčinu vs. následek a pěstitele vs. pozorovatele. Ale nikdy nekončíme; součástí zábavy je zjistit, jak můžeme rekapitulovat staré pojmy.

Šťastnou matematiku.

Příloha: Tady je návod, jak přemýšlet o změně základu

Tady je návod, jak přemýšlet o změně základu. Za předpokladu 100% spojitého růstu,

ln(x) je doba růstu na x
ln(2) je doba růstu na 2

Protože máme dobu růstu na dvojnásobek, můžeme zjistit, kolik by se jich „vešlo“ do celkové doby růstu na x:

$\displaystyle{\text{počet zdvojení od 1 do x} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

Kolik zdvojení nastane například od 1 do 64?

No, ln(64) = 4,158. A ln(2) = ,693. Počet dvojnásobků, které odpovídají, je:

$\displaystyle{\frac{\ln(64)}{\ln(2)} = \frac{4,158}{,693} = 6}$

V reálném světě mohou kalkulačky ztrácet přesnost, proto pokud je to možné, použijte přímou funkci logaritmu o základu 2. A samozřejmě můžeme mít i zlomkové číslo: Z 1 se dostaneme na druhou odmocninu z 2, což je „poloviční“ zdvojnásobení, neboli log2(1,414) = 0,5.

Přechod na logaritmický základ 10 znamená, že počítáme počet 10x-násobků, které se vejdou:

$\displaystyle{\text{počet 10x-násobků od 1 do x} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Je to dobré, že? Další příklady najdete v článku Použití logaritmů v reálném světě.

Další příspěvky v této sérii

Intuitivní průvodce exponenciálními funkcemi & e
Demytizace přirozeného logaritmu (ln)
Vizuální průvodce jednoduchými, složenými a spojitými úrokovými sazbami
Obvyklé definice e (vybarvené)
Pochopení exponentů (Proč 0^0 = 1?)
Použití logaritmů v reálném světě
Jak myslet pomocí exponentů a logaritmů
Pochopení diskrétního vs. spojitého růstu
Co vlastně znamená exponent
Q: Proč je e zvláštní? (2,718…, ne 2, 3,7 nebo jiné číslo?)