Hvordan man tænker med eksponenter og logaritmer

Her er et trick til at gennemtænke problemer, der involverer eksponenter og logaritmer. Du skal blot stille to spørgsmål:

1) Taler vi om input (årsag til ændringen) eller output (den faktiske ændring, der er sket?)

Logaritmer afslører de input, der forårsagede væksten
Eksponenter finder det endelige resultat af væksten

2) Taler vi om dyrkerens perspektiv eller en observatørs?

e og den naturlige logaritme er fra dyrkerens øjeblikkelige perspektiv
Base 10, base 2, osv. er målinger, der er bekvemme for en menneskelig observatør

I mit hoved sætter jeg mulighederne i en tabel:

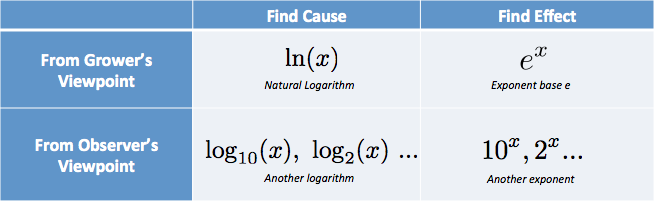
eksponent logaritme synspunkt sammenligning

Jeg har tanker som: “Jeg har brug for årsagen, fra dyrkerens perspektiv… det er den naturlige log.”. (Naturlig logaritme forkortes med små bogstaver LN, fra det højfede logaritmus naturalis.)

Jeg var frustreret over undervisning, der beskrev den indre del af tabellen, de rå funktioner, uden de billedtekster, der forklarede, hvornår man skulle bruge dem!

Det går ikke, lad os få direkte øvelse i at tænke med logaritmer og eksponenter.

Scenarie: Beskriv vækst i BNP

Her er et typisk eksempel på vækst:

Fra 2000 til 2010 ændrede USA’s BNP sig fra 9,9 billioner til 14,4 billioner

Okay, ja, de tal viser, at der skete ændringer. Men vi vil nok gerne have indsigt i årsagen: Hvilken gennemsnitlig årlig vækstrate ville være årsagen til denne ændring?

Med det samme tænker min hjerne “logaritmer”, fordi vi arbejder baglæns fra væksten til den hastighed, der forårsagede den. Jeg starter med en tanke som denne:

\displaystyle{\text{{logaritme af ændring} \rightarrow \text{årsag til vækst} }

En god start, men lad os skærpe den.

Først, hvilken logaritme skal vi bruge?

Som standard vælger jeg den naturlige logaritme. De fleste begivenheder ender med at være i termer af den voksende (ikke observatøren), og jeg kan godt lide at “køre med” det voksende element for at visualisere, hvad der sker. (Radians ligner: de måler vinkler i forhold til bevægeren.)

Næste spørgsmål: Hvilken ændring anvender vi logaritmen på?

Vi er egentlig bare interesseret i forholdet mellem start og slut: 9,9 billioner til 14,4 billioner på 10 år. Det er den samme vækstrate som at gå fra \$9,90 til \$14,40 i samme periode.

Vi kan skærpe vores tanke:

$\displaystyle{\text{naturlig logaritme af vækstforholdet} \rightarrow \text{årsag til vækst} }$

$\displaystyle{\ln(\frac{14.4}{9.9}) = .374}$

Ok, årsagen var en sats på .374 eller 37,4 %. Er vi færdige?

Ingen endnu. Logaritmer ved ikke noget om, hvor lang tid en ændring har taget (vi har jo ikke sat 10 år ind, vel?). De giver os en sats, som om hele ændringen skete i en enkelt tidsperiode.

Ændringen kunne faktisk være et enkelt år med 37,4 % kontinuerlig vækst eller 2 år med 18,7 % vækst eller en anden kombination.

Fra scenariet ved vi, at ændringen tog 10 år, så hastigheden må have været:

$\displaystyle{ \text{rate} = \frac{.374}{10} = .0374 = 3,74\%}$

Fra synspunktet om øjeblikkelig, kontinuerlig vækst voksede den amerikanske økonomi med 3,74% om året.

Er vi færdige nu? Ikke helt!

Denne kontinuerlige sats er set fra vækstens perspektiv, som om vi “kører med” økonomien, mens den ændrer sig. En bankmand interesserer sig sandsynligvis for den menneskevenlige forskel fra år til år. Vi kan finde ud af dette ved at lade den kontinuerlige vækst løbe i et år:

$\displaystyle{\text{eksponent med sats og tid} \rightarrow \text{effekt af vækst} }$

$\displaystyle{e^{\text{rate} \cdot \text{tid}} = \text{vækst}}}$

$\displaystyle{e^{.0374 \cdot 1} = 1.0381}$

Den årlige stigning er 3,8 %, hvilket er lidt højere end den øjeblikkelige sats på 3,74 % som følge af sammensætningen. Her er en anden måde at udtrykke det på:

Fra øjeblik til øjeblik vokser en given del af økonomien med 3,74 %, modelleret ved $e^(.0374 * år)$
På årsbasis, med sammensatte effekter udregnet, vokser økonomien med 3,81%, modelleret med $1.0381^år$

I finanssektoren ønsker vi måske den årlige ændring, som kan sammenlignes pænt med andre tendenser. Inden for videnskab og teknik foretrækker vi at modellere adfærd på øjeblikkelig basis.

Scenarie: Beskrive naturlig vækst

Jeg afskyr konstruerede eksempler som “Antag, at bakterier fordobles hver 24. time, find dens vækstformel.”. Replikerer bakteriekolonier sig med rene menneskelige intervaller, og skal vi vente på en nøjagtig fordobling?

Et bedre scenarie: “Hey, jeg fandt nogle bakterier, ventede en time, og klumpen voksede fra 2,3 gram til 2,32 gram. Jeg går til frokost nu. Regn ud, hvor meget vi har, når jeg er tilbage om 3 timer.”

Lad os lave en model af dette. Vi skal bruge en logaritme for at finde vækstraten og derefter en eksponent for at fremskrive denne vækst fremadrettet. Som tidligere skal vi holde alt i termer af den naturlige logaritme til at begynde med.

Vækstfaktoren er:

\displaystyle{\text{logaritme af ændring} \rightarrow \text{årsag til vækst} }

$\displaystyle{\ln(\text{vækst}) = \ln(2.32/2.3) = .0086 = .86\%}$

Det er satsen for en time, og den generelle model til fremskrivning vil være

$\displaystyle{{\text{eksponent med sats og tid} \rightarrow \text{effekt af vækst} }$

\displaystyle{e^{.0086 \cdot \text{timer}} \rightarrow \text{effekt af vækst} }

Hvis vi starter med 2,32 og vokser i 3 timer, får vi:

$\displaystyle{2,32 \cdot e^{.0086 \cdot 3} = 2,38}$

Selv for sjov, hvor lang tid går der, før bakterierne fordobles? Forestil dig at vente på, at 1 bliver til 2:

$\displaystyle{1 \cdot e^{.0086 \cdot \text{hours}}} = 2}$

Vi kan mekanisk tage den naturlige logaritme af begge sider for at “ophæve eksponenten”, men lad os tænke intuitivt.

Hvis 2 er det endelige resultat, så er ln(2) det vækstinput, der har bragt os dertil (en vis hastighed × tid). Vi ved, at hastigheden var 0,0086, så tiden for at nå til 2 vil være:

$\displaystyle{ \text{hours} = \frac{\ln(2)}{\text{rate}} = \frac{.693}{.0086} = 80,58}$

Kolonien vil fordobles efter ~80 timer. (Er du glad for, at du ikke blev hængende?)

Hvad betyder perspektivskiftet egentlig?

Det er ret ligetil at finde ud af, om du vil have input (årsag til vækst) eller output (resultat af væksten). Men hvordan visualiserer du vækstperspektivet?

Forestil dig, at vi har små arbejdere, der opbygger det endelige vækstmønster (se artiklen om eksponenter):

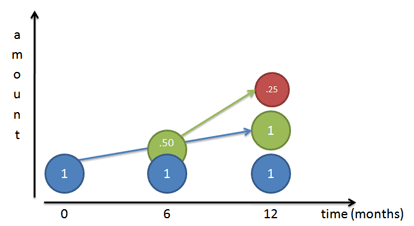
$Sammensat rente$

Hvis vores vækstrate er 100 %, fortæller vi vores oprindelige arbejder (hr. Blå), at han skal arbejde støt og skabe en 100 % kopi af sig selv ved årets udgang. Hvis vi følger ham dag for dag, kan vi se, at han faktisk færdiggør en 100 % kopi af sig selv (hr. Grøn) ved årets udgang.

Men… den arbejder, han var ved at bygge (hr. Grøn), begynder også at arbejde. Hvis hr. Green først dukker op ved 6-måneders-mærket, har han et halvt år til at arbejde (samme årlige hastighed som hr. Blue), og han bygger hr. Red. Selvfølgelig ender hr. rød med at være halvt færdig, da hr. grøn kun har 6 måneder.

Hvad nu, hvis hr. grøn dukkede op efter 4 måneder? En måned? En dag? Et sekund? Hvis arbejdstagerne begynder at vokse med det samme, får vi den øjeblikkelige kurve defineret ved $e^x$:

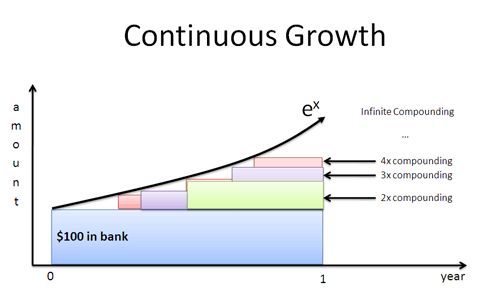
kontinuerlig vækst

Den naturlige log giver en vækstrate i forhold til den enkelte arbejdstagers perspektiv. Vi sætter denne sats ind i $e^x$ for at finde det endelige resultat, med al sammensætning inkluderet.

Anvendelse af andre baser

Skift til en anden type logaritme (base 10, base 2 osv.) betyder, at vi leder efter et mønster i den samlede vækst, ikke hvad den enkelte arbejder gør.

Hver logaritme stiller et spørgsmål, når vi ser en ændring:

Logbase e: Hvad var den øjeblikkelige hastighed, som den enkelte arbejder fulgte?
Logbase 2: Hvor mange fordoblinger var nødvendige?
Logbase 10: Hvor mange 10x-inger var nødvendige?

Her er et scenarie til analyse:

I løbet af 30 år er antallet af transistorer på typiske chips gået fra 1000 til 1 milliard

Hvordan vil du analysere dette?

Mikrochips er ikke en enkelt enhed, der vokser jævnt over tid. De er separate udgaver fra konkurrerende virksomheder og viser en generel teknologisk tendens.
Da vi ikke “rider med” på en voksende mikrochip, kan vi bruge en skala, der er lavet til menneskelig bekvemmelighed. Fordobling er nemmere at tænke på end 10x-ing.

Med disse antagelser får vi:

\displaystyle{\text{logaritme af ændring} \rightarrow \text{årsag til vækst} }

$\displaystyle{\log_2(\frac{\text{{1 milliard}}}{1000}) = \log_2(\text{1 million}) \sim \text{20 fordoblinger}$

“Årsagen til væksten” var 20 fordoblinger, som vi ved fandt sted over 30 år. Dette svarer i gennemsnit til 2/3 fordoblinger pr. år, eller 1,5 år pr. fordobling – en fin tommelfingerregel.

Fra dyrkerens perspektiv ville vi beregne $\ln(\text{1 milliard}/1000) / \text{30 år} = 46\%$ kontinuerlig vækst (lidt sværere at forholde sig til i dette scenarie).

Vi kan sammenfatte vores analyse i en tabel:

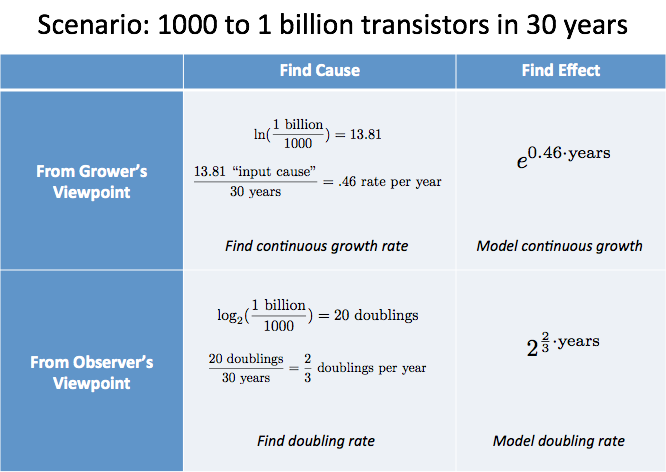
eksponenter transistor eksempel

Summary

Læring handler om at finde de skjulte billedtekster bag et begreb. Hvornår bruges det? Hvilket synspunkt bringer det ind i problemet?

Min nuværende fortolkning er, at eksponenter spørger om årsag vs. virkning og dyrker vs. observatør. Men vi er aldrig færdige; en del af det sjove er at se, hvordan vi kan rekapitulere gamle begreber.

Happy math.

Appendix: Formlen for baseændring

Her er en måde at tænke på at skifte base på. Hvis vi antager en 100% kontinuerlig vækstrate,

ln(x) er tiden til at vokse til x
ln(2) er tiden til at vokse til 2

Da vi har tiden til fordobling, kan vi se, hvor mange der ville “passe” i den samlede tid til at vokse til x:

$\displaystyle{\text{Antal fordoblinger fra 1 til x} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

For eksempel, hvor mange fordoblinger forekommer der fra 1 til 64?

Jamen, ln(64) = 4,158. Og ln(2) = ,693. Antallet af fordoblinger, der passer, er:

$\displaystyle{\frac{\ln(64)}{\ln(2)} = \frac{4,158}{.693} = 6}$

I den virkelige verden kan lommeregnerne miste præcision, så brug om muligt en direkte log base 2-funktion. Og selvfølgelig kan vi have et brøkregnet tal: At gå fra 1 til kvadratroden af 2 er “en halv” fordobling, eller log2(1,414) = 0,5.

Om vi skifter til log base 10 betyder det, at vi tæller antallet af 10x-ringer, der passer:

$\displaystyle{\text{antal 10x-ringer fra 1 til x} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Neat, right? Læs Brug af logaritmer i den virkelige verden for at få flere eksempler.

Andre indlæg i denne serie

En intuitiv guide til eksponentielle funktioner & e
Demystificering af den naturlige logaritme (ln)
En visuel guide til simple, sammensatte og kontinuerte rentesatser
Fælles definitioner af e (farvelagt)
Forståelse af eksponenter (Hvorfor er 0^0 = 1?)
Anvendelse af logaritmer i den virkelige verden
Sådan tænker man med eksponenter og logaritmer
Forståelse af diskret vs. kontinuerlig vækst
Hvad betyder en eksponent egentlig?
Q: Hvorfor er e specielt? (2,718…, ikke 2, 3,7 eller et andet tal?)