
Nurale netwerken en wiskunde zijn onafscheidelijk en dat is waarschijnlijk wat de meeste mensen afschrikt. Ik heb al te veel dubieuze opmerkingen gehoord over Deep Learning, “Oh dit is te veel wiskunde voor mij om te begrijpen”, “Hoeveel bedrijven gebruiken Deep Learning eigenlijk? Ik bespaar mezelf liever het hersenkraken en blijf weg van deze veeleisende concepten”.
Maar als je erover nadenkt, is het niet zo moeilijk. Geloof me! Om te begrijpen waarom een algoritme zich op een bepaalde manier gedraagt, is het van essentieel belang te begrijpen wat er achter de schermen gebeurt. Complexe algoritmen voor machinaal leren worden vandaag handig voor ons verpakt en zijn slechts een functie-oproep verwijderd. De afgeleiden van activeringsfuncties zijn iets minder voor de hand liggende concepten die we vaak geneigd zijn te negeren. Ze vormen echter de basis van krachtige algoritmen en een beetje extra moeite doen om ze te begrijpen loont zeker de moeite. Na het lezen van dit artikel bent u een stap dichter bij het ontrafelen van wat er onder de façade van de “zwarte doos” schuilgaat.
Achtergrond
Neurale netwerken maken gebruik van een verscheidenheid aan activeringsfuncties in de verborgen en output-lagen om het leerproces te katalyseren. Enkele veelgebruikte activeringsfuncties zijn de Sigmoid- en tanH-functies. De meest populaire activeringsfunctie is ReLU (Rectified Linear Unit) vanwege zijn vermogen om het probleem van de verdwijnende gradiënt effectief op te lossen. Een diepgaand inzicht in activeringsfuncties is voor een andere dag. Vandaag zullen we ons richten op de wiskunde achter de afgeleide van de Sigmoid functie.
Waarom is de afgeleide van een activeringsfunctie belangrijk?
Zoals u waarschijnlijk weet, worden neurale netwerken in twee stappen aangedreven:
- Voorwaartse Propagatie – De invoergegevens stromen door het netwerk en we krijgen de voorspelde uitvoer. We vergelijken het met de werkelijke output en berekenen de fout.
- Terug Propagatie – De berekende fout wordt gebruikt om de parameters van het neurale netwerk bij te werken met behulp van de afgeleide van de activeringsfunctie.
De Sigmoid Functie
De sigmoid functie, gekenmerkt door een S-vormige curve, wordt vaak aangeduid als een speciaal geval van de logistische functie. Zij is het nuttigst in gevallen waarin wij waarschijnlijkheid als output moeten voorspellen.
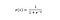
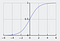
De sigmoid-functie geeft waarden die tussen 0 en 1 liggen (terecht gezien het feit dat het waarschijnlijkheden voorspelt).
De sigmoïde afgeleide
Deze fundamentele bouwsteen die helpt bij het trainen van neurale netwerken neemt de vorm aan:


Zo gauw mogelijk, laten we aan de slag gaan met de afgeleide!
Aanpak 1

Aanpak 2:
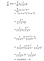
Waarom gebruiken we deze versie van het derivaat?
In de voorwaartse voortplantingsstap berekent u de sigmoïdefunctie (σ(x)) en hebt u de waarde ervan bij de hand. Bij het berekenen van de afgeleide in de backpropagation stap, hoef je alleen maar de waarde van σ(x) in de hierboven afgeleide formule te stoppen en voila, je bent klaar om te gaan!
Dat is het jongens! Bedankt voor het lezen!