How to Prepare for the Geometry Questions on a Math Test
General Information
Geometria to tylko fantazyjna nazwa dla badania linii i kształtów. Istnieją z pewnością dodatkowe trudne zasady i tematy, ale mamy podstawy tutaj. Trzeba będzie opanować te przed podjęciem bardziej zaawansowanych concepts.
(Please note that if a figure is labeled „example” in this guide, it may not be the only representation of that figure, but is one of them.)
Points and Lines
A point in geometry is a location. Nie ma on długości, szerokości, ani głębokości. Używamy kropki i dużej litery, aby pokazać punkt.
Odcinek linii jest zdefiniowany przez dwa punkty i wszystkie punkty między nimi. Te dwa punkty są nazywane punktami końcowymi odcinka. Odcinek ma jeden wymiar: długość. Aby napisać odcinek, należy umieścić kreskę nad dwoma punktami końcowymi. \odcinkiem jest odcinek:

Linia rozciąga się w obu kierunkach bez końca. Aby napisać prostą, należy umieścić pasek z dwiema strzałkami nad dowolnymi dwoma punktami prostej.

Promień zaczyna się w jednym punkcie końcowym i rozciąga się bez końca tylko w jednym kierunku. Aby napisać półprostą, należy umieścić słupek ze strzałką skierowaną w prawo nad dwoma punktami: punktem końcowym i dowolnym innym punktem (w tym kierunku). \W ten sposób powstaje półprosta:

Uwaga: nie można napisać półprostej ze strzałką skierowaną w lewo, tak jak w przypadku półprostej (overleftarrow{BA}}). Ważna jest też kolejność. \(\overrightarrow{BA}}) to nie to samo co \(\overrightarrow{AB}}). Pierwsza litera jest zawsze punktem początkowym półprostej.
Dwie proste, odcinki lub półproste są prostopadłe, jeśli tworzą kąt prosty (patrz poniżej). Do oznaczania prostopadłości używamy symbolu \(\). 
Dwie proste są równoległe, jeśli nigdy się nie przecinają. Jeżeli ∗ jest równoległa do ∗, to można napisać ∗ jest równoległa do ∗ jest równoległa do ∗).
Przykłady: 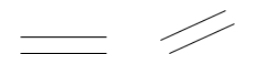
Kształty płaszczyznowe
W geometrii płaszczyzna jest płaską dwuwymiarową powierzchnią, która rozciąga się w nieskończoność. Te dwa wymiary to długość i szerokość. Więc, kształty płaszczyzny są „płaskie” kształty, takie jak kwadraty, koła i triangles.
Common Shapes
Poligon jest zamkniętą powierzchnią na płaszczyźnie ograniczonej przez odcinki linii zwanych sides.
Przykłady: 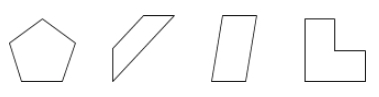
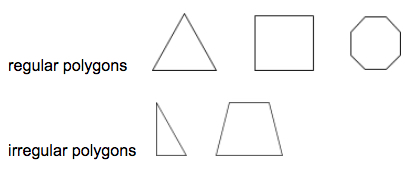
Wielokąt foremny to taki wielokąt, w którym wszystkie odcinki i kąty wewnętrzne są przystające.
Przykłady:
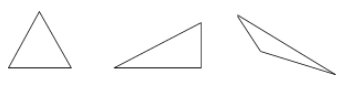
Trójkąt to wielokąt o trzech bokach.
Przykłady:
Czworokąty – wielokąty czteroboczne
Równoległobok jest rodzajem czworokąta, w którym przeciwległe boki są równoległe i przystające. Przeciwległe kąty równoległoboku są również przystające.
Przykłady: 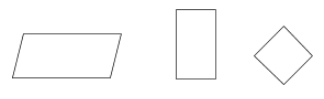
Prostokąt jest równoległobokiem o czterech kątach prostych.
Przykłady: 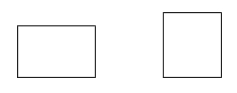
Romb to równoległobok, w którym wszystkie cztery boki są przystające.
Przykłady: 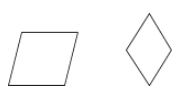
Kwadrat to równoległobok, który jest jednocześnie rombem i prostokątem (wszystkie boki są przystające i wszystkie kąty są proste).
Przykłady: 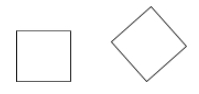
Trapez to czworokąt, który ma tylko jedną parę boków równoległych.
Przykłady: 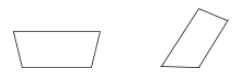
Poligony o więcej niż czterech bokach
Wielokąt o jedenastu bokach może być również nazywany endekogonem lub undekogonem.
Mierzenie kształtów
Obwód to całkowita odległość wokół wielokąta. Aby znaleźć obwód, wystarczy zsumować długości wszystkich boków. Jeśli wielokąt jest foremny (wszystkie boki są przystające), a długość jednego boku jest równa ∗, pomnóż liczbę boków przez ∗, aby znaleźć obwód. Na przykład, obwód pięciokąta foremnego wynosi ∗5s}
.