
As redes neurais e a matemática são inseparáveis e isso é provavelmente o que assusta a maioria das pessoas. Já ouvi demasiados comentários duvidosos sobre Aprendizagem Profunda, “Oh isto é demasiada matemática para eu compreender”, “Quantas empresas estão realmente a usar Aprendizagem Profunda? Eu prefiro poupar-me a mim mesmo de pensar e ficar longe desses conceitos exigentes”.
Mas se você pensar nisso, não é tão difícil assim. Confie em mim! Para entender porque um algoritmo se comporta de uma certa forma, é essencial compreender o que acontece nos bastidores. Algoritmos complexos de aprendizagem de máquina são empacotados convenientemente para nós hoje em dia e estão apenas a uma chamada de função de distância. As derivadas das funções de ativação são conceitos um pouco menos óbvios que muitas vezes tendemos a ignorar. No entanto, eles formam a base de algoritmos poderosos e colocar um pouco mais de esforço para compreendê-los certamente compensa. Depois de ler este artigo você estará um passo mais perto de desvendar o que está por baixo da fachada da “caixa preta”.
Background
Neural networks use uma variedade de funções de ativação nas camadas oculta e de saída para catalisar o processo de aprendizagem. Algumas das funções de ativação mais usadas incluem as funções Sigmoid e TanH. A função de ativação mais popular é a ReLU (Unidade Linear Retificada) por causa de sua capacidade de superar efetivamente o problema do gradiente de fuga. Uma visão aprofundada das funções de ativação é para outro dia. Hoje vamos focar na matemática por trás da derivada da função Sigmoid.
Por que é importante a derivada de uma função de ativação?
Como você provavelmente sabe, dois passos conduzem as redes neurais:
- Propagação Avançada – Os dados de entrada fluem através da rede e obtemos a saída prevista. Nós comparamos com a saída real e calculamos o erro.
- Propagação de retorno – O erro calculado é usado para atualizar os parâmetros da Rede Neural usando a derivada da função de ativação.
A função sigmóide
A função sigmóide, caracterizada por uma curva em forma de S, é frequentemente referida como um caso especial da função logística. Ela é mais útil nos casos em que temos que prever a probabilidade como saída.
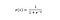
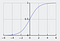
A função sigmoid produz valores que se situam entre 0 e 1 (corretamente considerando que ela prevê probabilidades).
A derivada sigmóide
Esta construção fundamental que ajuda a treinar redes neurais toma a forma:


Sem mais delongas, Vamos começar a derivação!
>
Aprova 1
 >
> >
>
>
Aprova 2:
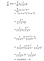
Por que usamos esta versão da derivada?
No passo de propagação para a frente, você calcula a função sigmóide (σ(x)) e tem o seu valor à mão. Enquanto calcula a derivada no passo de retropropagação, tudo o que você tem que fazer é conectar o valor de σ(x) na fórmula derivada acima e voilá, você está pronto para ir!
É isso aí pessoal! Obrigado por ler!