>
>
>
>
>
>
>
>
 >
>>>
>
>
Matemática trata de um grande número de conceitos que são muito importantes mas, ao mesmo tempo, complexos e demorados. Entretanto, Python fornece a biblioteca SciPy completa que resolve este assunto para nós. Neste tutorial SciPy, você estará aprendendo como fazer uso desta biblioteca juntamente com algumas funções e seus exemplos.
Antes de continuar, dê uma olhada em todos os tópicos discutidos neste artigo:
- O que é SciPy?
- NumPy vs SciPy
- Subpackages in SciPy
- Funções básicas
- Funções especiais
- Funções de integração
- Funções de optimização
- Funções de transformação de Fourier
- Sinal Funções de processamento
- Álgebra linear
- Valores próprios separados
- Estruturas e algoritmos de dados espaciais
- Funções de processamento de imagens multidimensionais
- Arquivo IO
Então vamos começar. 🙂
SciPy é uma biblioteca Python de código aberto que é usada para resolver problemas científicos e matemáticos. Ela é construída sobre a extensão NumPy e permite ao usuário manipular e visualizar dados com uma ampla gama de comandos de alto nível. Como mencionado anteriormente, SciPy é construída sobre NumPy e, portanto, se você importar SciPy, não há necessidade de importar NumPy.
NumPy vs SciPy
Both NumPy e SciPy são bibliotecas Python usadas para análise matemática e numérica usada. NumPy contém dados de array e operações básicas como ordenação, indexação, etc, enquanto que SciPy consiste de todo o código numérico. Apesar de NumPy fornecer uma série de funções que podem ajudar a resolver álgebra linear, transformação de Fourier, etc., SciPy é a biblioteca que realmente contém versões completas dessas funções, juntamente com muitas outras. No entanto, se você estiver fazendo análise científica usando Python, você precisará instalar tanto a NumPy quanto a SciPy, uma vez que a SciPy é construída sobre a NumPy.
Subpacotes em SciPy:
SciPy tem um número de subpacotes para vários cálculos científicos que são mostrados na seguinte tabela:
 >
>
>
>
>>
No entanto, para uma descrição detalhada, você pode seguir a documentação oficial.
Estes pacotes precisam ser importados exclusivamente antes de serem utilizados. Por exemplo:
from scipy import cluster
Antes de analisar cada uma destas funções em detalhes, vamos primeiro dar uma olhada nas funções que são comuns tanto em NumPy quanto em SciPy.
Interacção com NumPy:
SciPy se baseia em NumPy e portanto você pode fazer uso das próprias funções NumPy para lidar com arrays. Para conhecer a fundo sobre estas funções, você pode simplesmente fazer uso das funções help(), info() ou source().
help():
Para obter informações sobre qualquer função, você pode fazer uso da função help(). Existem duas maneiras de como esta função pode ser usada:
- Sem quaisquer parâmetros
- usando parâmetros
Aqui está um exemplo que mostra ambos os métodos acima:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
Quando você executa o código acima, a primeira help() retorna a informação sobre o submódulo do cluster. A segunda ajuda() pede ao usuário para digitar o nome de qualquer módulo, palavra-chave, etc para o qual o usuário deseja buscar informações. Para parar a execução desta função, simplesmente digite ‘quit’ e pressione enter.
info():
Esta função retorna informações sobre as funções desejadas, módulos, etc.
scipy.info(cluster)
source():
O código fonte é retornado somente para objetos escritos em Python. Esta função não retorna informações úteis caso os métodos ou objetos sejam escritos em qualquer outra linguagem como C. No entanto, caso você queira fazer uso desta função, você pode fazê-lo da seguinte forma:
scipy.source(cluster)
Funções Especiais:
SciPy fornece um número de funções especiais que são usadas em física matemática como elíptica, funções de conveniência, gama, beta, etc. Para procurar todas as funções, você pode fazer uso da função help() como descrito anteriormente.
Funções especiais e trigonométricas:
O pacote de funções especiais da SciPy fornece um número de funções através das quais você pode encontrar expoentes e resolver problemas trigonométricos.
Consulte o seguinte exemplo:
EXEMPLO:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
OUTPUT:
1000.0
8.0
1.0
0.7071067811865475
Há muitas outras funções presentes no pacote de funções especiais da SciPy que você pode tentar por si mesmo.
Funções de integração:
SciPy fornece um número de funções para resolver integrais. Variando do integrador diferencial comum ao uso de regras trapezoidais para calcular integrais, SciPy é um depósito de funções para resolver todos os tipos de problemas de integrais.
Integração Geral:
SiPy fornece uma função chamada quad para calcular a integral de uma função que tem uma variável. Os limites podem ser ( ) para indicar limites infinitos. A sintaxe da função quad() é a seguinte:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Aqui, a função será integrada entre os limites a e b (também pode ser infinita).
EXAMPLE:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
No exemplo acima, a função ‘a’ é avaliada entre os limites 0, 1. Quando este código é executado, você verá a seguinte saída.
OUTPUT:
(3.9086503371292665, 4.3394735994897923e-14)
Função Integral Dupla:
SciPy fornece dblquad que pode ser usado para calcular integrais duplas. Uma integral dupla, como muitos de nós sabemos, consiste em duas variáveis reais. A função dblquad() tomará a função a ser integrada como seu parâmetro junto com 4 outras variáveis que definem os limites e as funções dy e dx.
EXAMPLE:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
OUTPUT:
-1.3333333333333335, 1.4802973661668755e-14)
SciPy fornece várias outras funções para avaliar integrais triplos, n integrais, Romberg Integrais, etc que você pode explorar mais em detalhes. Para encontrar todos os detalhes sobre as funções necessárias, use a função de ajuda.
Optimization Functions:
The scipy.optimize fornece um número de algoritmos de otimização comumente usados que podem ser vistos usando a função de ajuda.
Consiste basicamente no seguinte:
- Minimização sem restrições e com restrições de funções escalares multivariadas, ou seja, minimizar (ex. BFGS, Newton Conjugate Gradient, Nelder_mead simplex, etc)
- Global optimization routines (ex. diferencial_evolução, recozimento_duplo, etc)
- Mínimização de mínimos_quadrados e ajuste de curvas (por exemplo, mínimos_quadrados, ajuste_de_curva, etc)
- Mínimizadores de funções univariadas de escalonamento e localizadores de raízes (por exemplo, BFGS, Newton Conjugate Gradient, Nelder_mead simplex, etc)
- Sistema de equações multivariadas usando algoritmos como o híbrido Powell, Levenberg-Marquardt.
minimize_scalar e root_scalar)
Função Rosenbrook:
Função Rosenbrook ( rosen) é um problema de teste usado para algoritmos de otimização baseados em gradientes. É definido da seguinte forma em SciPy:

EXEMPLO:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
OUTPUT: 7371.0399999999945
Nelder-Mead:
O método Nelder-Mead é um método numérico frequentemente utilizado para encontrar o min/max de uma função num espaço multidimensional. No exemplo seguinte, o método minimize é usado juntamente com o algoritmo Nelder-Mead.
EXAMPLE:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
OUTPUT: array()
Interpolation Functions:
No campo de análise numérica, interpolação refere-se à construção de novos pontos de dados dentro de um conjunto de pontos de dados conhecidos. A biblioteca SciPy consiste de um subpacote chamado scipy.interpolate que consiste de funções e classes spline, classes de interpolação unidimensional e multidimensional (univariada e multivariada), etc.
Interpolação Univariada:
Interpolação Univariada é basicamente uma área de ajuste de curva que encontra a curva que fornece um ajuste exato a uma série de pontos de dados bidimensionais. SciPy fornece a função interp1d que pode ser utilizada para produzir interpolação univariada.
EXAMPLE:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
OUTPUT:
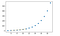
>
>>
Interpolação multivariada:
Interpolação multivariada (interpolação espacial ) é uma interpolação tipo em funções que consistem em mais de uma variável. O exemplo a seguir demonstra um exemplo de
Interpolando sobre uma grade 2-D usando a função interp2d(x, y, z) basicamente irá usar x, y, z arrays para aproximar alguma função interp2d. f: “z = f(x, y)” e retorna uma função cujo método de chamada usa interpolação spline para encontrar o valor de novos pontos.
EXAMPLE:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
OUTPUT:

Fourier Transform Functions:
Fourier analysis é um método que trata de expressar uma função como uma soma de componentes periódicos e recuperar o sinal a partir desses componentes. As funções fft podem ser usadas para retornar a transformação de Fourier discreta de uma seqüência real ou complexa.
EXAMPLE:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
OUTPUT:
Similiarmente, pode encontrar o inverso disto usando a função ifft da seguinte forma:
EXAMPLE:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
OUTPUT:
Funções de processamento de sinais:
O processamento de sinais trata de analisar, modificar e sintetizar sinais tais como som, imagens, etc. SciPy fornece algumas funções usando as quais você pode projetar, filtrar e interpolar dados unidimensionais e bidimensionais.
Filtragem:
Filtragem de um sinal, você basicamente remove componentes indesejados do mesmo. Para realizar a filtragem ordenada, você pode fazer uso da função order_filter. Esta função basicamente realiza a filtragem ordenada em um array. A sintaxe desta função é a seguinte:
SYNTAX:
filtro_de_ordem(a, domínio, classificação)
a = array de entrada N-dimensional
domain = array de máscara com o mesmo número de dimensões que `a`
rank = Número não-negativo que seleciona elementos da lista após ter sido ordenado (0 é o menor seguido por 1…)
EXAMPLE:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
>
Formas de onda:
A centelha.O subpacote de sinais também consiste em várias funções que podem ser usadas para gerar formas de onda. Uma dessas funções é o chirp. Esta função é um gerador de cosseno com frequência de rotação e a sintaxe é a seguinte:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)
where,

>
>
>
>>
from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
OUTPUT:

>
>
Álgebra linear:
Álgebra linear lida com equações lineares e suas representações usando espaços vetoriais e matrizes. SciPy é construída em bibliotecas ATLAS LAPACK e BLAS e é extremamente rápida na resolução de problemas relacionados à álgebra linear. Além de todas as funções do numpy.linalg, scipy.linalg também fornece uma série de outras funções avançadas. Além disso, se o numpy.linalg não é usado junto com ATLAS LAPACK e BLAS, scipy.linalg é mais rápido que o numpy.linalg.
Finding the Inverse of a Matrix:
Matematicamente, o inverso de uma matriz A é a matriz tal que onde está a matriz de identidade consistindo de uma diagonal abaixo da diagonal principal denotada como B=A-1. Em SciPy, este inverso pode ser obtido usando o método linalg.inv.
EXAMPLE:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
OUTPUT:
]
Encontrar os determinantes:
O valor derivado aritmeticamente dos coeficientes da matriz é conhecido como o determinante de uma matriz quadrada. Em SciPy, isto pode ser feito usando uma função det que tem a seguinte sintaxe:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
where,
a : (M, M) É uma matriz quadrada
overwrite_a( bool, opcional) : Permitir sobrescrever dados em a
check_finite ( bool, opcional): Para verificar se a matriz de entrada consiste apenas em números finitos
EXAMPLE:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
OUTPUT: -5.0
Sparse Eigenvalues:
Eigenvalues são um conjunto específico de escalares ligados com equações lineares. O ARPACK fornece que permitem encontrar auto-valores ( auto-valores ) bastante rápido. A funcionalidade completa do ARPACK é embalada dentro de duas interfaces de alto nível que são scipy.sparse.linalg.eigs e scipy.sparse.linalg.eigsh. eigs. A interface eigs permite encontrar os valores próprios de matrizes quadradas não simétricas reais ou complexas, enquanto que a interface eigsh contém interfaces para matrizes assimétricas reais ou complexas-hermitianas.
A oitava função resolve um problema de valor próprio generalizado para uma matriz hermitiana complexa ou simétrica real.
EXAMPLE:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
OUTPUT:
Selected eigenvalues :
Complexo ndarray :
]
Estruturas e Algoritmos de Dados Espaciais:
Dados espaciais consistem basicamente em objectos que são compostos por linhas, pontos, superfícies, etc. O pacote scipy.spatial da SciPy pode computar diagramas Voronoi, triangulações, etc usando a biblioteca Qhull. Ele também consiste de implementações KDTree para consultas de pontos vizinhos mais próximos.
Triangulações Delaunay:
Matematicamente, triangulações Delaunay para um conjunto de pontos discretos em um plano é uma triangulação tal que nenhum ponto no conjunto dado de pontos está dentro da circunferência de qualquer triângulo.
EXAMPLE:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
OUTPUT:

Funções de processamento de imagens multidimensionais:
O processamento de imagens trata basicamente de executar operações sobre uma imagem para recuperar informações ou para obter uma imagem melhorada da imagem original. O pacote scipy.ndimage consiste de um número de funções de processamento e análise de imagens concebidas para trabalhar com matrizes de dimensão arbitrária.
Convolução e correlação:
SciPy fornece um número de funções que permitem a correlação e convolução de imagens.
- A função correlate1d pode ser usada para calcular a correlação unidimensional ao longo de um dado eixo
- A função correlate permite a correlação multidimensional de qualquer array com o kernel especificado
- A função convolve1d pode ser usada para calcular a correlação unidimensional ao longo de um dado eixo
- A função correlate1d pode ser usada para calcular a correlação unidimensional ao longo de um dado eixoconvolução dimensional ao longo de um dado eixo
- A função convolve permite a convolução multidimensional de qualquer array com o kernel especificado
EXAMPLE:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
OUTPUT: array()
Arquivo IO:
A centelha.O pacote io fornece uma série de funções que ajudam a gerenciar arquivos de diferentes formatos como arquivos MATLAB, arquivos IDL, arquivos Matrix Market, etc.
Para fazer uso deste pacote, você precisará importá-lo da seguinte forma:
import scipy.io as sio
Para informações completas sobre o subpacote, você pode consultar o documento oficial em File IO.
Isto nos leva ao final deste Tutorial SciPy. Espero que você tenha entendido tudo claramente. Certifique-se de praticar o máximo possível.
Se você quiser conferir mais artigos sobre as tecnologias de maior tendência do mercado como Inteligência Artificial, DevOps, Ethical Hacking, então você pode consultar o site oficial do Edureka.
Procure outros artigos desta série que explicarão os vários outros aspectos do Python e da Data Science.
1. Classificação de Aprendizagem de Máquina em Python
2. Python Scikit-Learn Cheat Sheet
3. Ferramentas de Aprendizagem de Máquina
4. Bibliotecas Python para Ciência de Dados e Aprendizagem de Máquina
5. Chatbot em Python
6. Coleções Python
7. Módulos Python
8. Habilidades Python para desenvolvedores
9. OOPs Entrevista Perguntas e Respostas
10. Currículo para um desenvolvedor Python
11. Análise Exploratória de Dados em Python
12. Jogo da Cobra com o Módulo Python’s Turtle
13. Python Developer Salary
14. Análise dos componentes principais
15. Python vs C++
16. Tutorial de Scrapy
17. Raspagem da Web com Python
18. Método de Regressão dos mínimos quadrados
19. Jupyter Bloco de Notas de Jupyter
20. Noções básicas de Python
21. Programas Padrão Python
22. Geradores em Python
23. Decoradores em Python
24. Python Spyder IDE
25. Aplicações móveis usando Kivy em Python
26. Top 10 Best Books To Learn & Practice Python
27. Robot Framework Com Python
28. Jogo de Cobra em Python usando PyGame
29. Django Interview Questions and Answers
30. Top 10 Aplicações em Python
31. Tabelas de Hash e Hashmaps em Python
32. Python 3.8
33. Máquina Vetorial de Suporte
34. Python Tutorial